4D Gaussian Splatting (and HexPlane)

4D Gaussian Splatting for Real-Time Dynamic Scene Rendering (CVPR 2024)

4D Gaussian Splatting for Real-Time Dynamic Scene Rendering

Guanjun Wu, Taoran Yi, Jiemin Fang, Lingxi Xie, Xiaopeng Zhang, Wei Wei, Wenyu Liu, Qi Tian, Xinggang Wang

paper :
https://arxiv.org/abs/2310.08528
project website :
https://guanjunwu.github.io/4dgs/index.html
code :
https://github.com/hustvl/4DGaussians
referenced blog :
https://xoft.tistory.com/54

핵심 요약 :
3DGS를 dynamic scene에 적용하고자 할 때
x, y, z, t를 input으로 갖는 encoder로서
4D scene을 2D planes로 표현하는 HexPlane 기법을 이용하겠다!

Abstract

• spatially-temporally-sparse input으로부터
  complex point motion을 정확하게 모델링하면서
  high efficiency로 real-time dynamic scene을 rendering하는 건 매우 challenging task

• 3DGS를 각 frame에 적용하는 게 아니라 4DGS라는 새로운 모델 제시
  • 오직 3DGS 한 세트 필요
  • 4DGS framework :
    • Spatial-Temporal Structure Encoder :
      HexPlane [22] 에서 영감을 받아
      decomposed neural voxel encoding algorithm을 이용해서
      4D neural voxel을 2D voxel planes로 decompose하여
      2D voxel plane (param.)에 Gaussian point-clouds (pts)의 spatial-temporal 정보를 encode
    • Extremely Tiny Multi-head Gaussian Deformation Decoder :
      가벼운 MLP를 이용해서
      Gaussian deformation을 예측함
• 4DGS :
  real-time (82 FPS) rendering at high (800 \(\times\) 800) resolution on RTX 3090 GPU

Contribution

• Gaussian motion과 shape-deformation을 모두 모델링할 수 있는 4DGS framework 제시
  w. efficient Gaussian deformation field network

• multi-resolution encoding
  (only on spatial planes)
  (connect nearby 3D Gaussians to build rich Gaussian features)
  by efficient spatial-temporal structure encoder

• SOTA performance이면서 real-time rendering on dynamic scenes
  e.g. 82 FPS at resol. 800 \(\times\) 800 for synthetic dataset
  e.g. 30 FPS at resol. 1352 \(\times\) 1014 for real dataset

• 4D scenes에서의 editing 및 tracking에 활용 가능

Related Works

Novel View Synthesis

• static scene :
  • light fields [1], mesh [2] [3] [4] [5], voxels [6] [7] [8], multi-planes [9] 이용한 methods
  • NeRF-based methods NeRF MipNeRF [10]
• dynamic scene :
  • NeRF-based methods [11] [12] [13]
  • explicit voxel grid [14] [15] [16] [17] :
    temporal info. 모델링하기 위해 explicit voxel grid 사용
  • flow-based methods [18] [19] [16] [20] [21] :
    nearby frames를 blending하는 warping algorithm 사용
  • decomposed neural voxels [22] [23] [24] [25] [26] [27] :
    빠른 training on dynamic scenes 가능
    (Fig 1.의 (b))
  • multi-view setups 다루기 위한 methods [28] [29] [30] [31] [32] [33]
  • 본 논문 (4DGS) :
    위에서 언급된 methods는 빠른 training은 가능했지만 real-time rendering on dynamic scenes는 여전히 어려웠음
    \(\rightarrow\)
    본 논문은 빠른 training 및 rendering pipeline 제시
    (Fig 1.의 (c))

Fig 1. dynamic scene rendering methods

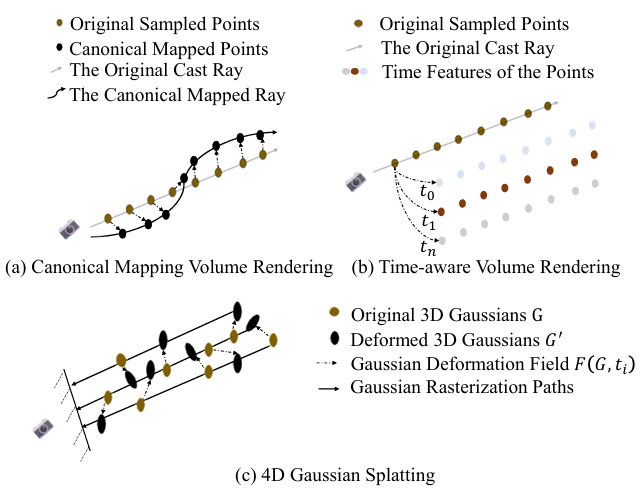
• Fig 1. 설명 :
  dynamic scene을 rendering하는 여러 방법들 소개
  • (a) : Deformation-based (Canonical Mapping) Volume Rendering
    point-deformation-field를 이용해서
    sampled points를 canonical space로 mapping
    (하나의 ray 위의 sampled points가 다같이 canonical space로 mapping되므로
    각 point의 서로 다른 속도를 잘 모델링하지 못함)
  • (b) : Time-aware Volume Rendering
    각 timestamp에서의 각 point의 feature를 직접 개별적으로 계산
    (path는 그대로)
  • (c) : 4DGS
    compact Gaussian-deformation-field를 이용해서
    기존의 3D Gaussians를 특정 timestamp의 3D Gaussians로 변환
    ((a)와 유사하긴 하지만
    각 Gaussian이 ray에 의존하지 않고 서로 다른 속도로 이동 가능)

Neural Rendering w. Point Clouds

• 3D scenes를 나타내기 위해 meshes, point-clouds, voxels, hybrid ver. 등 여러 분야가 연구되어 왔는데
  그 중 point-cloud representation을 volume rendering과 결합하면
  dynamic novel view synthesis task도 잘 수행 가능

• 3DGS :
  explicit representation이라서,
  differentiable point-based splatting이라서,
  real-time renderer라서 주목받음

• 3DGS on dynamic scenes :

  • Dynamic3DGS [34] :
    • 3D Gaussian 개수를 고정하고
      각 timestamp \(t_i\) 마다 각 3D Gaussian의 position, variance를 tracking
    • 문제점 :
      • need dense multi-view input images
      • prev. frame의 모델링이 부적절하면 전체적인 성능이 떨어짐
      • linear memory consumption \(O(tN)\)
        for \(t\)-time steps and \(N\)-3D Gaussians
  • 4DGS (본 논문) :
    • very compact network로 3D Gaussian motion을 모델링하기 때문에
      training 효율적이고 real-time rendering
    • memory consumption \(O(N+F)\)
      for \(N\)-3D Gaussians, \(F\)-parameters of Gaussian-deformation-field network
  • 4DGS (Zeyu Yang) [35] :
    • marginal temporal Gaussian 분포를 기존의 3D Gaussian 분포에 추가하여
      3D Gaussians를 4D로 uplift
    • However, 그러면 각 3D Gaussian은 오직 their local temporal space에만 focus
  • Deformable-3DGS (Ziyi Yang) [36] :
    • 본 논문처럼 MLP deformation network를 도입하여 dynamic scenes의 motion을 모델링
    • 본 논문 (4DGS)도 이와 유사하지만 training을 효율적으로 만듦
  • Spacetime-GS (Zhan Li) [37] :
    • 각 3D Gaussian을 individually tracking

Dynamic NeRF with Deformation Fields

• 모든 dynamic NeRF는 아래의 식을 따른다
  \(c, \sigma = M(x, d, t, \lambda)\)
  where \(c \in R^3, \sigma \in R, x \in R^3, d \in R^2, t \in R, \lambda \in R\)
  where \(\lambda\) is optional input (frame-dependent code to build topological and appearance changes) [12] [38]

• deformation NeRF-based methods는
  Fig 1. (a)에서처럼
  deformation network \(\phi_{t} : (x, t) \rightarrow \Delta x\) 로 world-to-canonical mapping 한 뒤
  RGB color와 volume density를 뽑는다
  \(c, \sigma = NeRF(x+\Delta x, d, \lambda)\)

• 4DGS (본 논문)은
  Gaussian deformation field network \(F\) 이용해서
  time \(t\) 에서의 canonical-to-world mapping을 직접 계산한 뒤
  differential splatting(rendering) 수행

Method

Overview (Gaussian Deformation Field Network)

Fig 2. Pipeline of this model (Gaussian Deformation Field Network)

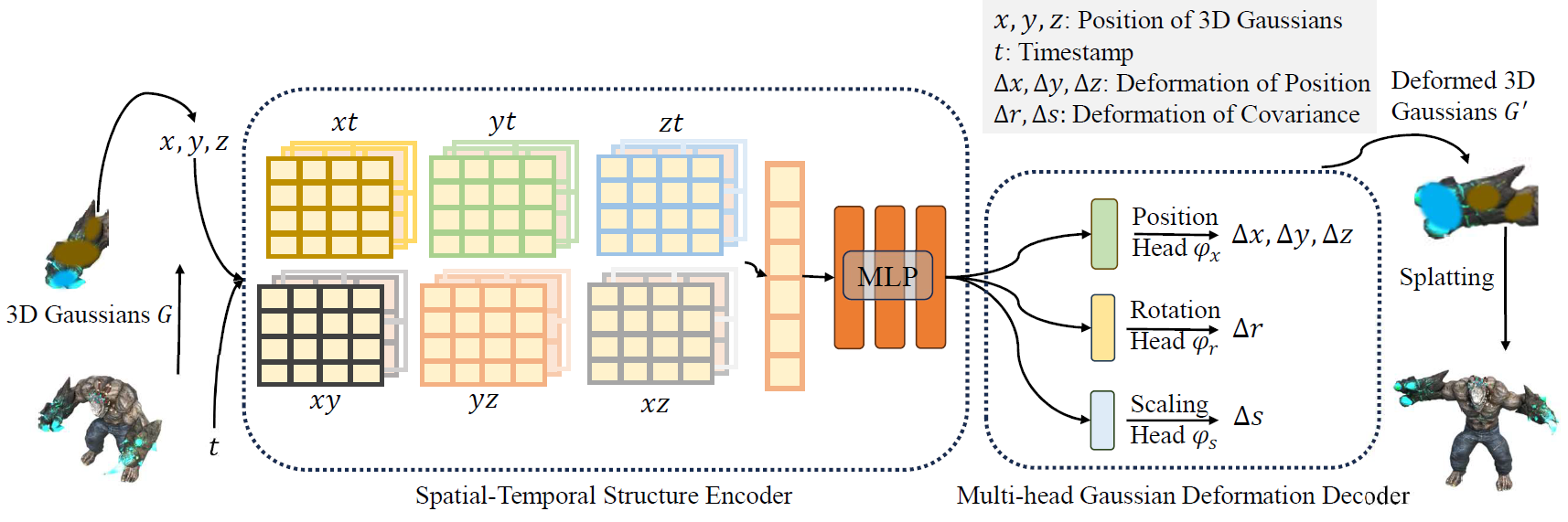
• Fig 2. 설명 :
  • static 3D Gaussian set을 만듦
  • 각 3D Gaussian의 center 좌표 \(x, y, z\) 와 timestamp \(t\) 를
    Gaussian Deformation Field Network의 input으로 준비
  • Spatial-Temporal Structure Encoder :
    multi-resolution voxel planes를 query하여
    voxel feature를 계산
    (temporal 및 spatial feature를 둘 다 encode 가능)
  • Tiny Multi-head Gaussian Deformation Decoder :
    position, rotation, scaling head에서 각각 해당 feature를 decode하여
    각 3D Gaussian의 position, rotation, scaling 변화량을 얻어서
    timestamp \(t\) 에서의 변형된 3D Gaussians를 얻음

Spatial-Temporal Structure Encoder

• 근처에 있는 3D Gaussians끼리는 항상 spatial 및 temporal 정보를 비슷하게 공유하고 있다.
  따라서 HexPlane 기법에서는 각 Gaussian이 따로 변형되는 게 아니라,
  여러 adjacent 3D Gaussian들이 군집처럼 연결되어 함께 변형되므로
  motion과 shape-deformation을 정확하게 예측할 수 있다
  이로써 변형된 geometry를 더 정확히 모델링하고 avulsion(벗겨짐?)을 방지할 수 있음

• 기존 논문 설명 (Backgrounds) :

  • TensoRF : Link
  • HexPlane [22] :
    4차원(\(XYZT\))을 모델링하기 위해
    3개 타입의 rank로 decomposition (\(XY\) 평면 - \(ZT\) 평면, \(XZ\) 평면 - \(YT\) 평면, \(YZ\) 평면 - \(XT\) 평면)

HexPlane Overview

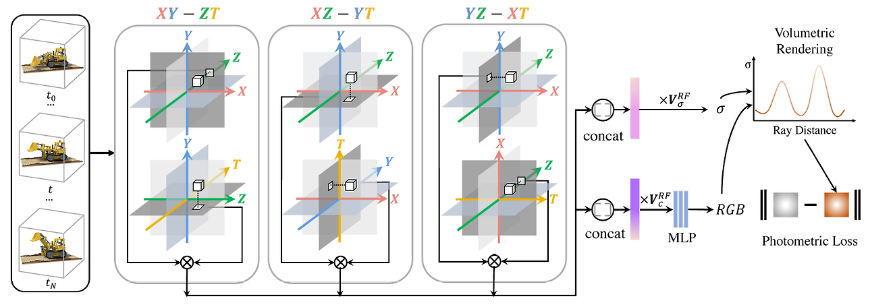
• Spatial-Temporal Structure Encoder (1) :
  • vanilla 4D neural voxel은 memory를 많이 잡아먹기 때문에
    4D neural voxel(\(XYZT\))을 6개의 multi-resol. planes로 decompose하는
    4D K-Planes module [23] 사용
  • 3D Gaussians는 bounding plane voxels에 포함되어
    Gaussians의 deformation도 nearby temporal voxels에 encode될 수 있음 ????
  • 기존 논문들 [14] [22] [23] [26] 에서 영감을 받아
    Spatial-Temporal Structure Encoder는
    multi-resolution HexPlane \(R(i, j)\) 와 tiny MLP \(\phi_{d}\) 로 구성됨

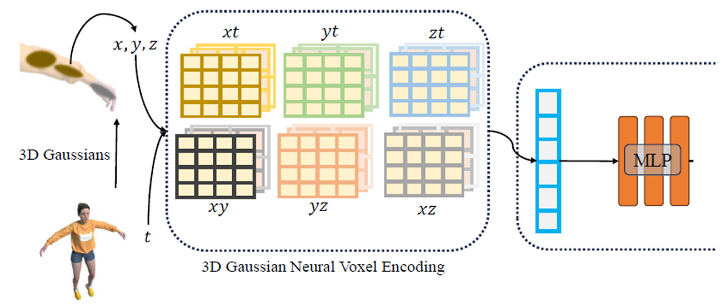
• Spatial-Temporal Structure Encoder (2) :
  • multi-resolution HexPlane \(R(i, j)\) :
    본 논문에서는 TensoRF와 달리 Grid resol.을 점점 증가시키지 않고, 애초에 multi-resolution으로 decomposition의 rank를 구성함
    \(f_{h} = \cup_{l} \prod \text{interp}(R_{l}(i, j))\)
    • where
      \(f_h \in R^{h \ast l}\) : feature of decomposed neural voxel
      \(R_{l}(i, j) \in R^{h \times lN_i \times lN_j}\) : 2D voxel plane (nn.Parameter())
      \(h\) : hidden dim.
      \(\{ i, j \} \in \{ (x, y), (x, z), (y, z), (x, t), (y, t), (z, t) \}\) : 6 종류의 planes
      \(N\) : voxel grid의 basic resol.
      \(l \in \{ 1, 2 \}\) : upsampling scale (multi-resol.)
      \(\text{interp}\) : bilinear interpolation (plane의 grid의 네 꼭짓점으로부터 interpolation으로 voxel feature 뽑아냄)
      \(\prod\) : product over planes (K-Planes [23] 참고)
      \(\cup_{l}\) : multi-resol.에 대해 concat 또는 add
    • Github Code 에서
      • forward()
      • get_density()
        • self.grids : multi-resol. HexPlane
          즉, nn.ModuleList() of init_grid_param()
        • init_grid_param() : HexPlane
          즉, nn.ParameterList() of nn.Parameter()
          where
          range(in_dim) = [0, 1, 2, 3] (x, y, z, t) 중에 grid_nd = 2개의 조합(plane)을 뽑아서
          각 nn.Parameter()는 2D grid plane \(R_{l}(i, j)\) for \(\{ i, j \} \in \{ (x, y), (x, z), (y, z), (x, t), (y, t), (z, t) \}\)
          w. shape \((1, D_{out}, \text{resol.}[j], \text{resol.}[i])\)
          e.g. \(R_{l}(x, t)\), 즉 \(XT\) plane은 nn.Parameter()
          w. shape \((1, D_{out}, \text{resol.}[3], \text{resol.}[0])\)
      • interpolate_ms_features() : \(f_{h} = \cup_{l} \prod \text{interp}(R_{l}(i, j))\) 반환
      • grid_sample_wrapper() : \(\text{interp}(R_{l}(i, j))\) 반환
      • grid_sampler() : F.grid_sample() Link
        second argument(pts) 좌표에서의 값을 구하기 위해 first argument(grid \(R_{l}(i, j)\))의 값을 interpolate
        그럼 이제 dynamic 3D scene을 4D neural voxel 대신 2D voxel plane \(R_{l}(i, j)\) 이라는 param.들로 표현 가능
• Spatial-Temporal Structure Encoder (3) :
  • tiny MLP \(\phi_{d}\) :
    \(f_d = \phi_{d} (f_h)\)
    merge all the features
  • 공간상(e.g. \(XY\) 평면) 또는 시간상(e.g. \(XT\) 평면)으로 인접한 voxel은
    HexPlane \(R(i, j)\) 에서 유사한 feature를 가져서 유사한 Gaussian param. 변화량을 가지므로
    optimization 진행됨에 따라
    Gaussian의 covariance가 줄어들면서 작은 3D Gaussian들이 모여서 dense해진다 ?????

Extremely Tiny Multi-head Gaussian Deformation Decoder

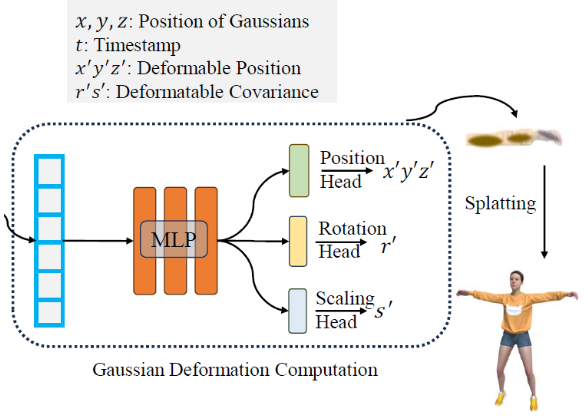
• Multi-head Gaussian Deformation Decoder :
  • 매우 작은 multi-head decoder로 position, scaling, rotation 변화량을 얻음
    \(\Delta \chi = \phi_{x}(f_d)\)
    \(\Delta r = \phi_{r}(f_d)\)
    \(\Delta s = \phi_{s}(f_d)\)
  • 그러면 변형된 deformed 3D Gaussians 계산할 수 있음
    \((\chi ' , r ' , s ') = (\chi + \Delta \chi, r + \Delta r, s + \Delta s)\) 에 대해
    next time \(t\) 의 deformed 3D Gaussian set은
    \(G ' = \{ \chi ' , r ' , s ', \sigma, c \}\)
  • 근데 실제 implementation 할 때는 speed 증가 위해
    scaling(size), rotation, color, opacity는 고정하고
    position 변화량만 구함
  • Github Code 에서
    • Class deform_network()의 forward_dynamic()
    • Class Deformation()의 forward_dynamic()
      • hidden : encoder(HexPlane과 MLP) 거쳐 얻은 feature
      • self.pos_deform, self.scales_deform, self.rotations_deform : tiny Multi-head decoder
        hidden으로부터 \(\Delta \chi, \Delta r, \Delta s\) 얻음
      • self.static_mlp :
        hidden으로부터 \(\text{mask}\) 얻음
      • position :
        \(\chi ' = \gamma(\chi) \times \text{mask} + \Delta \chi\)
      • scaling :
        \(s ' = \gamma(s) \times \text{mask} + \Delta s\)
      • rotation :
        \(r ' = \gamma(r) + \Delta r\)
        또는
        \(r ' =\) quaternion product of \(\gamma(r)\) and \(\Delta r\)
      • opacity, SH 도 deform 가능하게 짜놓긴 함
        \(\alpha ' = \alpha \times \text{mask} + \Delta \alpha\)
        \(k ' = k \times \text{mask} + \Delta k\)

self._deformation = deform_network(args)

Optimization

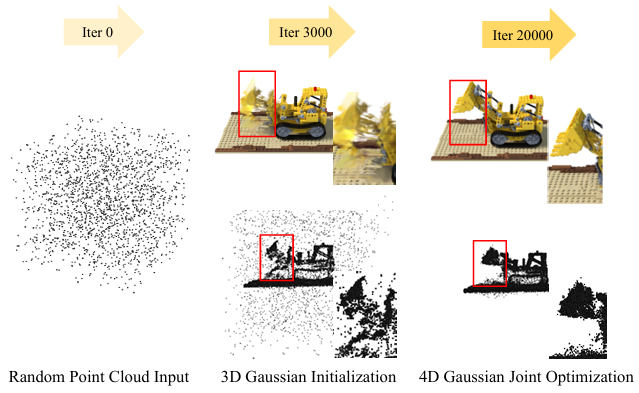
• warm-up :
  처음 3000 iter. 동안은
  Gaussian Deformation Field Network 없이
  3DGS의 SfM points initialization 이용하여
  static 3DGS optimize 하고,
  그 후에 dynamic scene에 대해 4DGS framework를 fine-tuning 형태로 학습

• Loss :
  \(L = | \hat I - I | + L_{tv}\)

  • L1 recon. loss
  • total-variational loss :
    • sparse input images일 경우에 적게 관측된 view에서는 noise 및 outlier 때문에 overfitting 및 local minima 문제가 발생할 수 있으므로
      regularization term 필요
    • pixel 값 간의 급격한 변화를 억제하기 위해
      \(I_{i+1, j} - I_{i, j}\) 항과 \(I_{i, j+1} - I_{i, j}\) 항을 loss에 추가

Experiment

• single RTX 3090 GPU

• Synthetic Dataset :

  • designed for monocular settings
  • camera poses for each timestamp은 거의 randomly generated 수준
  • scene 당 50-200 frames

• Real-world Dataset :
  • by HyperNeRF [12] and Neu3D [25]
  • HyperNeRF dataset :
    one or two cameras
    with straightforward camera motion
    (1,2개의 camera를 직관적인 경로로 움직이며 촬영)
  • Neu3D dataset :
    15 to 20 static cameras
    with extended periods and complex camera motions
    (15-20개의 많은 정적인 camera로 오랜 시간 동안씩 촬영하며 복잡한 경로로 camera를 움직임)

Results

• Metrics :
  • quality :
    PSNR
    LPIPS
    SSIM
    DSSIM
    MS-SSIM
  • speed :
    FPS
    training times
  • memory :
    storage

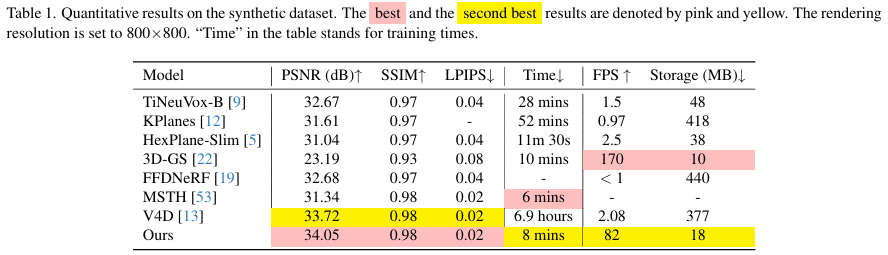
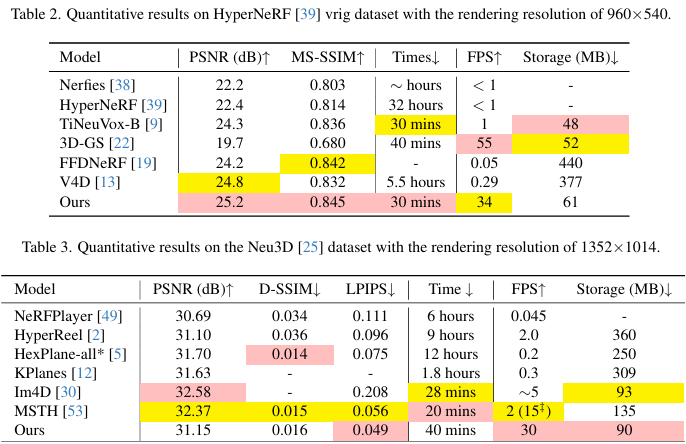
• Im4D [29] 는 본 논문과 유사하게 high-quality이지만
  multi-cam 방식을 쓰기 때문에 monocular scene을 모델링하기 어렵

Ablation Study

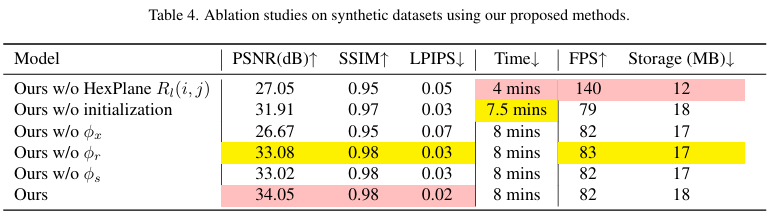
• Spatial-Temporal Structure Encoder :
  • explicit HexPlane encoder는
    3DGS의 spatial 및 temporal 정보를 모두 encode 하면서
    purely explicit method [34] 보다 storage 공간 아낄 수 있음
  • 만약에 HexPlane encoder 없이 shallow MLP encoder만 쓰면
    복잡한 deformation 모델링 어렵
• 3D Gaussian Initialization :
  • 처음에 warm-up으로 SfM points initialization 한 뒤 static 3DGS optimize 부터 해야
    아래의 장점들 있음
    • 3DGS 일부가 dynamic part에 분포되도록 함
    • 3DGS를 미리 학습해야 deformation field가 dynamic part에 더 집중 가능
    • deformation field 학습 시 numerical errors를 방지하여 훈련 과정이 더 stable
• Multi-head Gaussian Deformation Decoder :
  • 3D Gaussian motion을 modeling함으로써 dynamic scene을 잘 표현할 수 있도록 해줌

• Neural Voxel Encoder :
  • implicit MLP-based neural voxel encoder (voxel grid)가 아니라
    explicit Dynamic 3DGS 기법을 사용할 경우
    rendering quality는 떨어지지만 FPS 및 storage는 향상
• Two-stage Training :
  • static 3DGS stage \(\rightarrow\) dynamic 4DGS stage (fine-tuning) 으로
    분할해서 학습할 경우 성능 향상
    (참고로 D-NeRF, DyNeRF에서는 point-clouds가 주어지지 않아서 어려운 task를 다룸)
• Image-based Loss :
  • LPIPS loss, SSIM loss 같은 image-based loss를 사용할 경우
    training speed도 느려지고 quality도 떨어짐
  • 그 이유는
    image-based loss로 motion 부분을 fine-tuning하는 건 어렵고 복잡
• Model Capacity (MLP size) :
  • voxel plane resol. 또는 MLP 크기가 증가할수록
    quality 향상되지만 FPS 및 storage 악화
• Fast Training :
  • 7k iter. 까지만 학습해도(training 시간 짧음) 괜찮은 PSNR 달성

Discussion

• Tracking with 3D Gaussians :
  • Dynamic3DGS [34] 와 달리
    본 논문은 monocular setting에서도 low storage로 3D object tracking 가능
    (e.g. 10MB for 3DGS and 8MB for deformation field network)

• Composition(Editing) with 4D Gaussians :
  • Dynamic3DGS [34] 에서처럼
    4DGS editing 가능

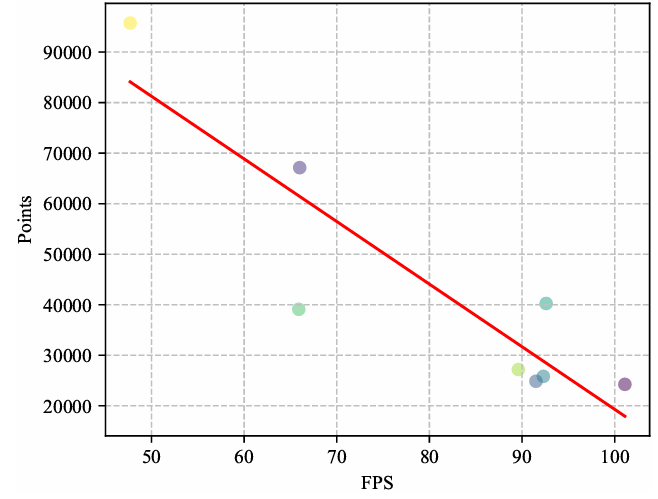
• Rendering Speed (FPS) :
  • 3DGS 수와 FPS는 반비례 관계인데
    Gaussians 수가 30,000개 이하이면 single RTX 3090 GPU에서 90 FPS 까지 가능
  • 이처럼 real-time FPS를 달성하려면
    resolution, Gaussian 수, Gaussian deformation field network 용량, hardware constraints 등 여러 요인을 조절해야 함

Limitation

• 아래의 경우엔 학습 잘 안 됨
  • large motions일 경우
  • background points가 없을 경우
  • camera pose가 unprecise(부정확)할 경우

• 추가적인 supervision 없이
  static Gaussians와 dynamic Gaussians의 joint motion을 구분하는 건 아직 어려운 과제

• urban(large)-scale recon.일 경우엔
  3DGS 수가 훨씬 많아서
  Gaussian deformation field network를 query하기에 너무 무거우므로 좀 더 compact한 algorithm이 필요

Conclusion

• 4DGS framework for real-time dynamic scene rendering

• efficient deformation field network to model motions and shape-deformation
  • Spatial-temporal structure encoder :
    adjacent Gaussians가 비슷하게 encode되도록 spatial-temporal 정보를 encode
  • Multi-head Gaussian deformation decoder :
    position, scaling, rotation을 각각 modeling
• dynamic scenes 모델링 뿐만 아니라
  4D object tracking 및 editing에도 활용 가능

Question

• Q1 : 본 논문을 한 문장으로 요약하자면,
  3DGS를 dynamic scene에 적용하고자 할 때 4D 정보를 효율적으로 encode하기 위해 2D planes로 scene을 표현하는 HexPlane 기법을 이용하겠다!인데,
  본 논문이 novelty가 있는지 의구심이 듭니다.

• A1 : 3DGS 논문 자체가 나온 지 얼마 안 돼서
  기존 논문(HexPlane) 아이디어를 3DGS에 적용하는 논문들이 아직까지는 많이 채택되는 것 같다.

• Q2 : 본 포스팅에서 코드 리뷰는 encoder (HexPlane) 쪽만 진행하였는데,
  Multi-head Gaussian deformation decoder로 position, scaling, rotation 변화량을 구해서
  Deformed(변형된) 3DGS를 구하는 부분의 코드도 보고 싶습니다.
• A2 : 포스팅의 “Extremely Tiny Multi-head Gaussian Deformation Decoder” 부분에 해당 내용을 추가하였습니다.

Appendix

• TBD