DDPM

Diffusion Study

Diffusion

Diffusion Model

• forward process : fixed Gaussian noise 더함
• reverse process : learned Gaussian noise 뺌 (mean, std를 학습)

Likelihood

아래 둘 다 관측값 \(x\)가 나올 확률인데,

• probability \(P(x | \theta)\) : 확률 분포가 고정된 상태에서, 관측되는 사건이 변화할 때의 확률
  예: 선택 가능한 정수를 1~5로 제한(확률 분포 고정)했을 때, 관측 목표값이 1~5 중 한 개의 숫자(관측 사건 변화)일 경우

• likelihood \(L(\theta | x)\) : 관측된 사건이 고정된 상태에서, 확률 분포 몰라서 가정할 때의 확률
  예: 선택 가능한 정수를 1~5가 아니라 1~10 또는 4~50으로 바꾸면서(확률 분포 모름), 2가 관측될 확률을 계산(관측 사건 고정)할 경우
  예: 어떤(모르는) 확률 분포를 따르는 task를 n회 반복 수행하여 관측했을 때 random var. 종류를 가정할 수도 있고 특정 random var.의 parameter를 가정할 수도 있다

• 주어진 대상이 training data \(D\) 이고, 구하고자 하는 대상이 model param. \(w\) 일 때

  • Posterior : $$P(w

    D)$$

  • Likelihood : $$P(D

    w)$$

  • Prior : \(P(w)\)
• 주어진 대상이 input image \(X_0\) 이고, 구하고자 하는 대상이 noisy image \(X_T\) 일 때

  • Posterior : $$P(X_{T}

    X_{0})$$

  • Likelihood : $$P(X_{0}

    X_{T})$$

  • Prior : \(P(X_T)\)

Markov process

• Markov process (= Markov chain = memoryless process) : Markov property를 가지는 discrete stochastic process
  \(P[s_{t+1}|s_t] = P[s_{t+1}|s_1, \ldots, s_t]\)

KL-divergence

• \(H(p, q) = - \sum p_i log q_i\) : 두 확률분포 p, q의 cross entropy
  (보통 \(p\)는 GT, \(q\)는 predicted)
• \(H(p) = - \sum p_i log p_i\) : p’s entropy (상수값)
• \(KL(p \| q) = H(p, q) - H(p) = \sum p_i log \frac{p_i}{q_i}\) : 두 확률분포 p, q의 차이
  \(H(p)\)는 상수값이므로 KL-divergence minimize = cross entropy minimize
• 모르는 분포 \(p(x)\)를 N개 sampling하여 trained \(q(x | \theta)\)로 근사하고자 할 때,
  \(KL(p \| q) \simeq \frac{1}{N} \sum_{n=1}^{N} {-log q(x_n | \theta) + log p(x_n)}\) :
  \(log p(x_n)\)은 \(\theta\)에 독립이므로 KL-divergence minimize = negative log likelihood minimize = MLE

KL-diverence 특성 :

1. \(KL(p \| q) \geq 0\) : 확률분포 p = q일 때 최소
2. \(KL(p \| q) \neq KL(q \| p)\) (asymmetric) : 거리 개념이 아님
   거리 개념으로 쓰는 방법 : 2가지 KL-divergence를 평균내는 방식의 \(JSD(p \| q)\)

Diffusion Algorithm

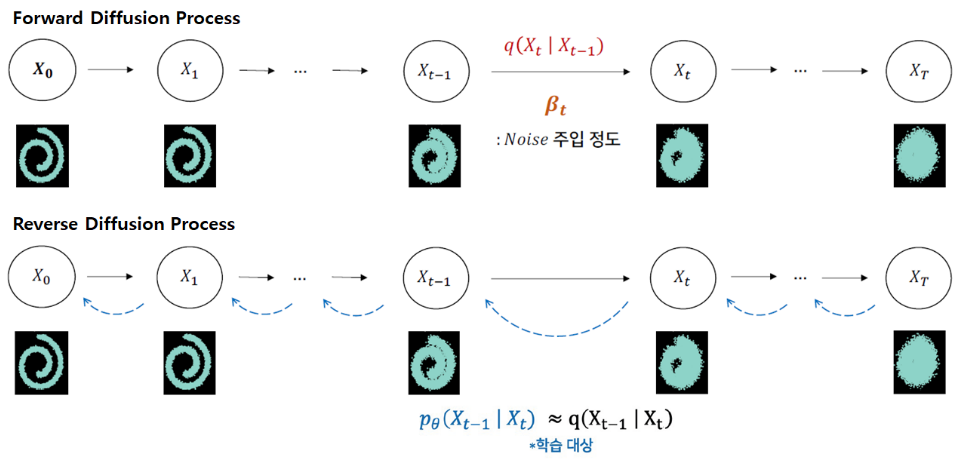
• forward process (\(q\)) :
  \(q(X_t | X_{t-1}) = N(X_t ; \mu_{X_{t-1}}, \Sigma_{X_{t-1}}) = N(X_t ; \sqrt{1-\beta_t} \cdot X_{t-1}, \beta_t \cdot I)\)
  where \(\beta_t\) : noise 주입 정도 (상수값)
  t가 증가할수록 \(\beta_t\)가 증가하여 다른 pixel(\(I\))을 선택하므로 noise가 강해진다

• backward process (\(p_{\theta}\)) :
  inference 할 때 image prior \(q(X_t)\)를 모르기 때문에 \(q(X_{t-1} | X_t)\)를 계산할 수 없다. (intractable)
  하지만 train 할 때는 forward process에서 더해지는 noise 정보 (GT) 를 알고 있으므로 \(q(X_{t-1} | X_t, X_0)\)를 계산할 수 있다. (tractable)
  목표 : \(q(X_{t-1} | X_t, X_0)\)를 근사하는 \(p_{\theta}(X_{t-1} | X_t)\)를 학습하여 inference할 때 사용하자!
  즉, 확률분포 \(q\)에서 관측한 값 \(x\)로 \(p_{\theta | x}\)의 likelihood (그럴 듯한 정도) 를 구했을 때 그 값이 최대가 되도록 하는 MLE Problem
  즉, minimize \(E_q [- log p_{\theta} (x_0)]\)

• Diffusion Model Naive Loss 수식 :
  확률분포 \(q\)로 sampling했을 때,
  \(E_{x_T \sim q(x_T|x_0)}[- log p_{\theta}(x_0)] \leq\)
  \(E_q [D_{KL}(q(x_T | x_0) \| p_{\theta} (x_T)) + \sum_{t \gt 1} D_{KL}(q(x_{t-1} | x_t, x_0) \| p_{\theta} (x_{t-1} | x_t)) - log p_{\theta} (x_0 | x_1)]\)

• DDPM(Denoising Diffusion Probabilistic Model)(2020) Loss 수식 :
  \(E_{t, x_0, \epsilon} [\| \epsilon - \epsilon_{\theta}(\sqrt{\bar \alpha_{t}}x_0 + \sqrt{1-\bar \alpha_{t}} \epsilon, t) \|^{2}]\)
  where \(\epsilon \sim N(0, I)\)
  즉, \(\epsilon_{\theta}\)가 Standard Gaussian 분포 \(\epsilon\)를 따르도록!
  이 때, \(\epsilon_{\theta}\)의 input은 \(q(x_t | x_0)\)와 \(t\) !

• Distribution Summary :

Let \(\alpha_t = 1 - \beta_t\) and \(\bar \alpha_t = \prod_{s=1}^t \alpha_s\) and \(\epsilon \sim N(0, I)\)

1. \[x_t \sim q(x_t | x_{t-1}, x_0) = q(x_t | x_{t-1}) = N(x_t ; \sqrt{\alpha_{t}} \cdot x_{t-1}, \beta_{t} \cdot \boldsymbol I)\]
2. \[x_t \sim q(x_t | x_0) = N(x_t; \sqrt{\bar \alpha_{t}} x_{0}, (1-\bar \alpha_{t}) \boldsymbol I) = \sqrt{\bar \alpha_{t}}x_0 + \sqrt{1-\bar \alpha_{t}} \epsilon\]

3. \(x_{t-1} \sim q(x_{t-1} | x_t, x_0) = N(x_{t-1}; \tilde \mu_{t}(x_t), \tilde \beta_{t})\)
   where \(\tilde \mu_{t}(x_t) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{t}) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \frac{x_t - \sqrt{\bar \alpha_{t}}x_0}{\sqrt{1-\bar \alpha_{t}}}) = \cdots = \sqrt{\bar \alpha_{t-1}} \frac{\beta_{t}}{1 - \bar \alpha_{t}} x_0 + \sqrt{\alpha_{t}} \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} x_t\)
   and \(\tilde \beta_{t} = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t}\)

4. \(x_{t-1} \sim p_{\theta}(x_{t-1} | x_t) = N(x_{t-1}; \mu_{\theta}(x_t, t), \tilde \beta_{t}) = \mu_{\theta}(x_t, t) + \tilde \beta_{t} \epsilon\)
   where \(\mu_{\theta}(x_t, t) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{\theta}(x_t, t)) = \cdots = \sqrt{\bar \alpha_{t-1}} \frac{\beta_{t}}{1 - \bar \alpha_{t}} x_0 + \sqrt{\alpha_{t}} \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} x_t\)
   and \(\tilde \beta_{t} = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t}\)
   (training param.로 학습하는 부분은 \(\epsilon_{\theta}(x_t, t)\) 뿐!!)

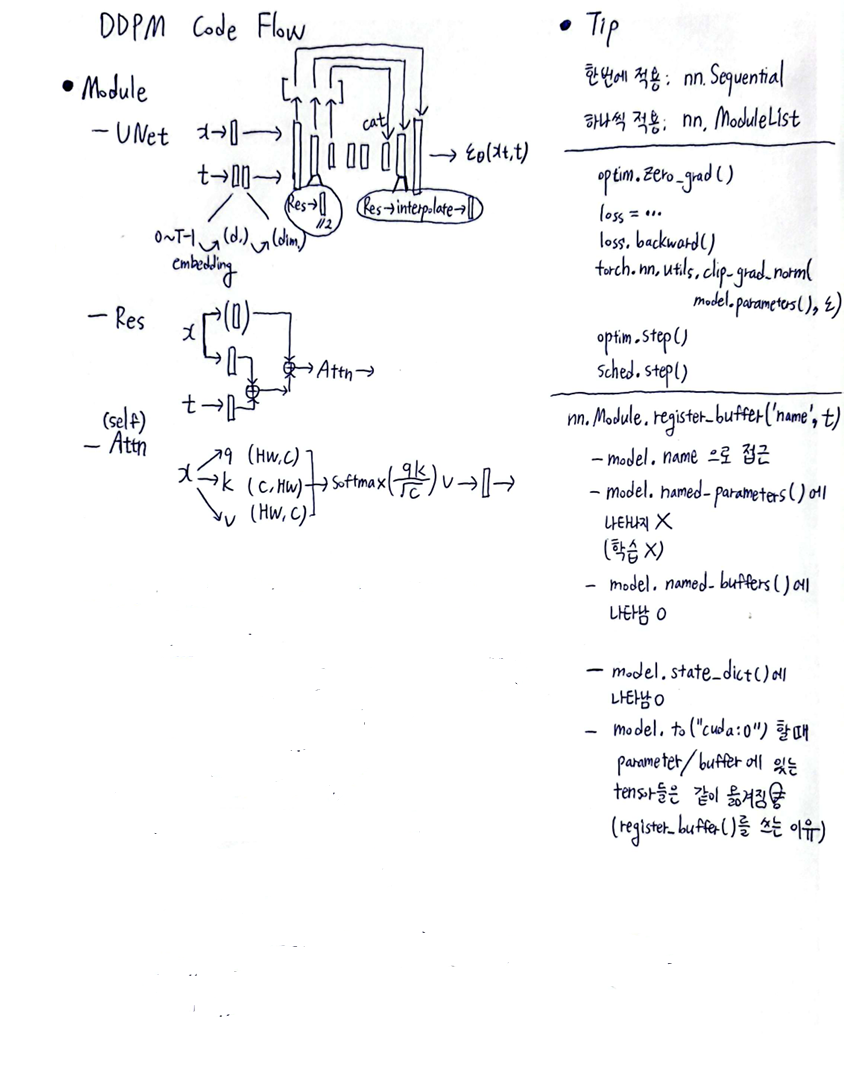
DDPM Diagram

reference : Link

• Model : U-Net \(\supset\) Res Block \(\supset\) Self-Attention

• Tip :

  • nn.Module들 그룹 지을 때
    한 번에 forward하려면 nn.Sequential
    하나씩 꺼내서 forward하려면 nn.ModuleList
  • nn.Module class 내에서 \(\text{self.register_buffer('name', t)}\) :
    • model.name 으로 t에 접근
    • model.named_parameters() 에 나타나지 않음 (학습 X)
    • model.named_buffers() 에 나타남
    • model.state_dict() 에 나타남
    • model.to(“cuda:0”) 할 때 parameters()와 buffers()에 있는 tensor들은 같이 옮겨짐!!
      이것이 \(\text{self.register_buffer('name', t)}\) 를 하는 이유!!

• Trainer :
  • DDPM의 forward process를 구현하여 U-Net을 훈련시킴
  • \(x_0\) 로부터 random \(t\) 에 대해 \(x_t = \sqrt{\bar \alpha_{t}}x_0 + \sqrt{1-\bar \alpha_{t}} \epsilon\) 를 구해서
    self.model로 \(\epsilon_{\theta}(x_t, t)\) 를 예측한 뒤
    \(\epsilon\) 과의 차이로 loss 구함
• Sampler :
  • DDPM의 backward process를 구현하여 inference(sampling)에 쓰임
  • self.model이 예측한 \(\epsilon_{\theta}(x_t, t)\) 를 이용해서
    \(x_T\) 로부터 \(x_{T-1}, \cdots, x_0\) 구함
    • \(x_{t-1} = \mu_{\theta}(x_t, t) + \tilde \beta_{t} \epsilon\)
      where \(\mu_{\theta}(x_t, t) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{\theta}(x_t, t)) = \cdots = \sqrt{\bar \alpha_{t-1}} \frac{\beta_{t}}{1 - \bar \alpha_{t}} x_0 + \sqrt{\alpha_{t}} \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} x_t\)
      and \(\tilde \beta_{t} = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t}\)

Diffusion Model 및 DDPM Loss 수식 유도

Step 1. ELBO (Evidence Lower Bound) 꼴로 변환

\(log p_{\theta}(x_0)\)
\(= E_{x_T \sim q(x_T|x_0)}[log p_{\theta}(x_0)]\)
\(= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{p_{\theta}(x_{0:T})}{p_{\theta}(x_{1:T}|x_0)}]\)
\(= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}] + E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{1:T}|x_0)}] \cdots (\ast)\)
(\(p_{\theta}(x_{1:T}|x_0)\)은 intractable하므로 KL divergence 항에 넣어서 제거!)

마지막 식의 오른쪽 항은 아래와 같이 KL divergence 꼴이다.
\(E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{1:T}|x_0)}] = \sum q(x_{1:T}|x_0) log \frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{1:T}|x_0)} = D_{KL}(q(x_{1:T}|x_0) \| p_{\theta}(x_{1:T}|x_0))\)
\(q(x_{1:T}|x_0)\)는 계산할 수 있지만 \(p_{\theta}(x_{1:T}|x_0)\)는 계산할 수 없으므로 KL divergence의 특성 \(KL(p \| q) \geq 0\)을 이용하면
\((\ast)\) 으로부터
\(log p_{\theta}(x_0) \geq E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}]\)
즉, \(E_{x_T \sim q(x_T|x_0)}[- log p_{\theta}(x_0)] \leq E_{x_{1:T} \sim q(x_{1:T}|x_0)}[- log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}]\)

Step 2. Markov property 이용하여 Diffusion Model Naive Loss 유도

\[E_{x_{1:T} \sim q(x_{1:T}|x_0)}[- log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}]\] \[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{0:T})}]\] \[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{\prod_{t=1}^{T} q(x_t|x_{t-1})}{p_{\theta}(x_T) \prod_{t=1}^T p_{\theta}(x_{t-1}|x_t)}]\]

by memoryless Markov chain property

\[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[- log p_{\theta}(x_T) + \sum_{t=1}^{T} log \frac{q(x_t|x_{t-1})}{p_{\theta}(x_{t-1}|x_t)}]\] \[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[- log p_{\theta}(x_T) + \sum_{t=2}^{T} log \frac{q(x_t|x_{t-1})}{p_{\theta}(x_{t-1}|x_t)} + log \frac{q(x_1|x_0)}{p_{\theta}(x_0|x_1)}]\] \[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[- log p_{\theta}(x_T) + \sum_{t=2}^{T} log \frac{q(x_t|x_{t-1}, x_0)}{p_{\theta}(x_{t-1}|x_t)} + log \frac{q(x_1|x_0)}{p_{\theta}(x_0|x_1)}]\]

by memoryless Markov property
어떻게든 계산 가능하도록 (tractable하도록) 만들기 위해 \(q(x_t|x_{t-1})\) 의 조건부에 \(x_0\) 추가

\[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[- log p_{\theta}(x_T) + \sum_{t=2}^{T} log (\frac{q(x_{t-1}|x_t, x_0)}{p_{\theta}(x_{t-1}|x_t)} \cdot \frac{q(x_t|x_0)}{q(x_{t-1}|x_0)}) + log \frac{q(x_1|x_0)}{p_{\theta}(x_0|x_1)}]\]

by Bayes 정리
\(P(A|B \bigcap C) = \frac{P(B|A \bigcap C) \cdot P(A|C)}{P(B|C)}\)

\(= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[- log p_{\theta}(x_T) + \sum_{t=2}^{T} log \frac{q(x_{t-1}|x_t, x_0)}{p_{\theta}(x_{t-1}|x_t)} + log \frac{q(x_T|x_0)}{q(x_1|x_0)} + log \frac{q(x_1|x_0)}{p_{\theta}(x_0|x_1)}]\)
by log 곱셈으로 소거

\[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[log \frac{q(x_T|x_0)}{p_{\theta}(x_T)} + \sum_{t=2}^{T} log \frac{q(x_{t-1}|x_t, x_0)}{p_{\theta}(x_{t-1}|x_t)} - log p_{\theta}(x_0|x_1)]\] \[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[D_{KL}(q(x_T|x_0) \| p_{\theta}(x_T)) + \sum_{t=2}^{T} D_{KL}(q(x_{t-1}|x_t, x_0) \| p_{\theta}(x_{t-1}|x_t)) - log p_{\theta}(x_0|x_1)]\]

by KL divergence 식 \(D_{KL}(P \| Q) = \sum P(x) log (\frac{P(x)}{Q(x)})\)

Step 3. DDPM Loss 유도

1. \(L_T = D_{KL}(q(x_T | x_0) \| p(x_T))\) : regularization loss
   마지막 상태 \(x_T\)에서 확률분포 q, p의 차이를 최소화
   noise 주입 정도인 \(\beta_t\)는 미리 정해둔 schedule에 따른 상수값(fixed)이므로
   \(q(x_T | x_0)\)는 training과 관계없이 \(x_T\)가 항상 Gaussian 분포를 따르도록 한다.
   \(x_T\)가 Gaussian 분포를 따르므로 \(q(x_T | x_0)\)와 \(p(x_T)\)는 거의 유사하고,
   결과적으로 둘의 KL divergence인 \(L_T\)는 항상 0에 가까운 값을 가지므로 training에서 \(L_T\) term은 제외

2. \(L_{t-1} = D_{KL}(q(x_{t-1} | x_t, x_0) \| p(x_{t-1} | x_t))\) : denoising process loss
   현재 상태 \(x_t\)가 주어질 때 이전 상태 \(x_{t-1}\)가 나올 확률 분포 q, p의 차이를 최소화

3. \(L_0 = - log p_{\theta} (x_0 | x_1)\) : reconstruction loss
   q를 sampling했을 때 \(p_{\theta} (x_0 | x_1)\)를 최대화하여 (MLE) 확률분포 q, p의 차이를 최소화
   전체적으로 봤을 때 \(L_0\)는 무수히 많은 time step \(T \sim 1000\) 중 단일 시점에서의 log likelihood 값이므로
   값이 너무 작아서 training에서 \(L_0\) term은 제외

Let’s only minimize the second term
\(E_{x_{1:T} \sim q(x_{1:T}|x_0)}[\sum_{t=2}^{T} L_{t-1}] = E_{x_{1:T} \sim q(x_{1:T}|x_0)}[\sum_{t=2}^{T} D_{KL}(q(x_{t-1} | x_t, x_0) \| p(x_{t-1} | x_t))]\)

Step 4. Gaussian param. \(\mu, \sigma\)로 KL-divergence 나타내기

• Gaussian Integral :
  \(\int_{-\infty}^{\infty} e^{-x^2}dx = \sqrt{\pi}\) and \(\int_{-\infty}^{\infty} x^2 e^{-ax^2}dx = \frac{1}{2}\sqrt{\pi}a^{-\frac{3}{2}}\)

• Integral of \(p(x)logp(x)\) for Gaussian \(p(x)\) :
  For \(p(x) = \frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} e^{-\frac{(x-\mu_{1})^2}{2 \sigma_{1}^2}} \sim N(\mu_{1}, \sigma_{1})\),
  \(\int p(x) log p(x) dx\)
  \(= \int \frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} e^{-\frac{(x-\mu_{1})^2}{2 \sigma_{1}^2}} log (\frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} e^{-\frac{(x-\mu_{1})^2}{2 \sigma_{1}^2}}) dx\)
  \(= \int \frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} e^{-t^2} (log \frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} - t^2) \sqrt{2} \sigma_{1} dt\)
  by 치환 \(t = \frac{x-\mu_{1}}{\sqrt{2}\sigma_{1}}\)
  \(= \frac{1}{\sqrt{\pi}} \int e^{-t^2} (log \frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} - t^2) dt\)
  \(= - \frac{log(2\pi \sigma_{1}^{2})}{2 \sqrt{\pi}} \int e^{-t^2} dt - \frac{1}{\sqrt{\pi}} \int t^2 e^{-t^2} dt\)
  \(= - \frac{log(2\pi \sigma_{1}^{2})}{2 \sqrt{\pi}} \cdot \sqrt{\pi} - \frac{1}{\sqrt{\pi}} \cdot \frac{\sqrt{\pi}}{2}\) by Gaussian integral
  \(= - \frac{log(2\pi \sigma_{1}^{2})}{2} - \frac{1}{2}\)
  \(= - \frac{1}{2} (1 + log(2\pi \sigma_{1}^{2}))\)

• Integral of \(p(x)logq(x)\) for Gaussian \(p(x)\) and \(q(x)\) :
  For \(p(x) = \frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} e^{-\frac{(x-\mu_{1})^2}{2 \sigma_{1}^2}} \sim N(\mu_{1}, \sigma_{1})\)
  and \(q(x) = \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} e^{-\frac{(x-\mu_{2})^2}{2 \sigma_{2}^2}} \sim N(\mu_{2}, \sigma_{2})\),
  \(\int p(x) log q(x) dx\)
  \(= \int p(x) log \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} e^{-\frac{(x-\mu_{2})^2}{2 \sigma_{2}^2}} dx\)
  \(= \int p(x) log \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} dx - \int p(x) \frac{(x-\mu_{2})^2}{2 \sigma_{2}^2} dx\)
  \(= log \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} - \int p(x) \frac{(x-\mu_{2})^2}{2 \sigma_{2}^2} dx\)
  \(= log \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} - \frac{\int p(x) x^2 dx - \int 2 \mu_{2} x p(x) dx + \mu_{2}^2 \int p(x) dx}{2 \sigma_{2}^2}\)
  \(= log \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} - \frac{E_{1}(x^2) - 2 \mu_{2} E_{1}(x) + \mu_{2}^2}{2 \sigma_{2}^2}\)
  \(= log \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} - \frac{\sigma_{1}^2 + \mu_{1}^2 - 2 \mu_{2} \mu_{1} + \mu_{2}^2}{2 \sigma_{2}^2}\)
  by \(Var(X) = E[X^2] - (E[X])^2\)
  \(= - \frac{1}{2} log (2 \pi \sigma_{2}^{2}) - \frac{\sigma_{1}^2 + (\mu_{1} - \mu_{2})^2}{2 \sigma_{2}^2}\)

• KL divergence for Gaussian \(p(x)\) and \(q(x)\) :
  For \(p(x) = \frac{1}{\sqrt{2 \pi \sigma_{1}^{2}}} e^{-\frac{(x-\mu_{1})^2}{2 \sigma_{1}^2}} \sim N(\mu_{1}, \sigma_{1})\)
  and \(q(x) = \frac{1}{\sqrt{2 \pi \sigma_{2}^{2}}} e^{-\frac{(x-\mu_{2})^2}{2 \sigma_{2}^2}} \sim N(\mu_{2}, \sigma_{2})\),
  \(D_{KL}(p \| q)\)
  \(= \int p(x) log \frac{p(x)}{q(x)} dx\)
  \(= \int p(x) logp(x) dx - \int p(x) log q(x)dx\)
  \(= - \frac{1}{2} (1 + log(2\pi \sigma_{1}^{2})) - (- \frac{1}{2} log (2 \pi \sigma_{2}^{2}) - \frac{\sigma_{1}^2 + (\mu_{1} - \mu_{2})^2}{2 \sigma_{2}^2})\)
  \(= - \frac{1}{2} + \frac{1}{2} log (\frac{2 \pi \sigma_{2}^2}{2 \pi \sigma_{1}^2}) + \frac{\sigma_{1}^2 + (\mu_{1} - \mu_{2})^2}{2 \sigma_{2}^2}\)
  \(= - \frac{1}{2} + log (\frac{\sigma_{2}}{\sigma_{1}}) + \frac{\sigma_{1}^2 + (\mu_{1} - \mu_{2})^2}{2 \sigma_{2}^2}\)

Step 5. Only Minimize the second term in Diffusion Loss

\[E_{x_{1:T} \sim q(x_{1:T}|x_0)}[\sum_{t=2}^{T} L_{t-1}]\] \[= E_{x_{1:T} \sim q(x_{1:T}|x_0)}[\sum_{t=2}^{T} D_{KL}(q(x_{t-1} | x_t, x_0) \| p(x_{t-1} | x_t))]\]

Let \(\sigma\) std have no learning param. (상수값)
Let \(q(x_{t-1} | x_t, x_0)\) have Gaussian mean \(\tilde \mu_{t}\)
Let \(p_{\theta}(x_{t-1} | x_t)\) have Gaussian mean \(\mu_{\theta}\)

By Step 4., since \(\sigma\) is fixed, we have to minimize

\[E_{x_{1:T} \sim q(x_{1:T}|x_0)}[\frac{1}{2 \sigma_{t}^2} \| \tilde \mu_{t} (x_t, x_0) - \mu_{\theta} (x_t, t) \|^2] + C\]

Now we have to know \(\tilde \mu_{t}\) and \(\mu_{\theta}\)

Step 6. Obtain \(q(x_t \| x_0)\) from \(q(x_t \| x_{t-1})\)

1. Let’s define \(q(x_t | x_{t-1}) = N(x_t ; \sqrt{1-\beta_{t}} \cdot x_{t-1}, \beta_{t} \cdot \boldsymbol I)\)
   where noise 주입 비율인 \(\beta_{t}\)는 t에 따라 증가하는 상수값이고,
   noise 주입 비율이 커질수록 분산이 커지는 건 reasonable

2. Let’s define \(\alpha_{t} = 1 - \beta_{t}\) and \(\bar \alpha_{t} = \prod_{s=1}^t \alpha_{s}\)
   where \(\bar \alpha_{t}\)는 \(s=1\)부터 \(s=t\)까지 \(\alpha_{s} = 1 - \beta_{s}\)의 누적곱

When \(\epsilon_{t-1}, \epsilon_{t-2}, \cdots, \epsilon_0 \sim N(0, I)\),
\(x_t = \mu + \sigma \cdot \epsilon = \sqrt{\alpha_{t}} x_{t-1} + \sqrt{1-\alpha_{t}} \cdot \epsilon_{t-1}\)
\(\cdots\)
\(x_t = \sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1-\bar \alpha_{t}} \cdot \epsilon\)
where \(\epsilon \sim N(0, I)\)
by merging two Gaussians \(N(0, \sigma_{1}^2 I), N(0, \sigma_{2}^2 I) \rightarrow N(0, (\sigma_{1}^2 + \sigma_{2}^2) I)\)

Therefore,
\(q(x_t | x_0) = N(x_t; \sqrt{\bar \alpha_{t}} x_{0}, (1-\bar \alpha_{t}) \boldsymbol I)\)

즉, 우리가 정의한 Gaussian \(q(x_t \| x_{t-1})\) 으로부터 Gaussian \(q(x_t\|x_0)\) 를 얻어냈다!

Step 7. Obtain \(q(x_{t-1} \| x_t, x_0)\)

Remind that

1. \[q(x_t | x_{t-1}, x_0) = q(x_t | x_{t-1}) = N(x_t ; \sqrt{\alpha_{t}} \cdot x_{t-1}, \beta_{t} \cdot \boldsymbol I)\]
2. \[q(x_t | x_0) = N(x_t; \sqrt{\bar \alpha_{t}} x_{0}, (1-\bar \alpha_{t}) \boldsymbol I)\]

\(q(x_{t-1} | x_t, x_0)\)
\(= q(x_t | x_{t-1}, x_0) \frac{q(x_{t-1} | x_0)}{q(x_t | x_0)}\)
\(\propto \exp (- \frac{(x_t - \sqrt{\alpha_{t}} x_{t-1})^2}{2 \beta_{t}} - \frac{(x_{t-1} - \sqrt{\bar \alpha_{t-1}} x_{0})^2}{2 (1-\bar \alpha_{t-1})} + \frac{(x_{t} - \sqrt{\bar \alpha_{t}} x_{0})^2}{2 (1-\bar \alpha_{t})})\)
\(= \exp (- \frac{1}{2} ((\frac{\alpha_{t}}{\beta_{t}} + \frac{1}{1 - \bar \alpha_{t-1}})x_{t-1}^2 - (\frac{2 \sqrt{\alpha_t}}{\beta_{t}} x_t + \frac{2\sqrt{\bar \alpha_{t-1}}}{1 - \bar \alpha_{t-1}} x_0) x_{t-1} + C(x_t, x_0)))\)

\(q(x_{t-1} | x_t, x_0)\) 또한 Gaussian이라서
\(\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}\) 꼴이므로
\(q(x_{t-1} | x_t, x_0)\)의 지수부분을 \(x_{t-1}\)에 대한 이차식 꼴로 정리하면
계수 비교를 통해 \(q(x_{t-1} | x_t, x_0)\)의 mean, variance를 알 수 있음!

• \(q(x_{t-1} | x_t, x_0)\) 의 variance :
  \(\frac{1}{\sigma^{2}}\)
  \(= \frac{\alpha_{t}}{\beta_{t}} + \frac{1}{1 - \bar \alpha_{t-1}}\)
  \(= \frac{\alpha_{t} - \alpha_{t} \bar \alpha_{t-1} + \beta_{t}}{\beta_{t}(1 - \bar \alpha_{t-1})}\)
  \(= \frac{\alpha_{t} - \bar \alpha_{t} + 1 - \alpha_{t}}{\beta_{t}(1 - \bar \alpha_{t-1})}\)
  \(= \frac{1 - \bar \alpha_{t}}{\beta_{t}(1 - \bar \alpha_{t-1})}\)

따라서 \(\sigma^{2} = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t}\)

• \(q(x_{t-1} | x_t, x_0)\) 의 mean :
  \(- \frac{2 \mu}{\sigma^{2}}\)
  \(= - (\frac{2 \sqrt{\alpha_t}}{\beta_{t}} x_t + \frac{2\sqrt{\bar \alpha_{t-1}}}{1 - \bar \alpha_{t-1}} x_0)\)
  \(\rightarrow \mu = (\frac{\sqrt{\alpha_t}}{\beta_{t}} x_t + \frac{\sqrt{\bar \alpha_{t-1}}}{1 - \bar \alpha_{t-1}} x_0) \cdot \sigma^{2}\)
  \(= (\frac{\sqrt{\alpha_t}}{\beta_{t}} x_t + \frac{\sqrt{\bar \alpha_{t-1}}}{1 - \bar \alpha_{t-1}} x_0) \cdot (\frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t})\)
  \(= \frac{\sqrt{\alpha_t} x_t (1 - \bar \alpha_{t-1}) + \beta_{t} x_0 \sqrt{\bar \alpha_{t-1}}}{\beta_{t}(1 - \bar \alpha_{t-1})} \cdot (\frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t})\)
  \(= \frac{\sqrt{\alpha_t} x_t (1 - \bar \alpha_{t-1}) + \beta_{t} x_0 \sqrt{\bar \alpha_{t-1}}}{1 - \bar \alpha_{t}}\)

따라서
\(\mu = \frac{\sqrt{\bar \alpha_{t-1}} \beta_{t}}{1 - \bar \alpha_{t}} x_0 + \frac{\sqrt{\alpha_t} (1 - \bar \alpha_{t-1})}{1 - \bar \alpha_{t}} x_t\)

\(q(x_t | x_0) = N(x_t; \sqrt{\bar \alpha_{t}} x_{0}, (1-\bar \alpha_{t}) \boldsymbol I)\)이므로
방금 구한 \(\mu\) 식에서 \(x_0\) 소거하기 위해
\(x_t = \sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1-\bar \alpha_{t}} \epsilon\) 대입하면

\(\mu_{t} = \frac{\sqrt{\bar \alpha_{t-1}} \beta_{t}}{1 - \bar \alpha_{t}} x_0 + \frac{\sqrt{\alpha_t} (1 - \bar \alpha_{t-1})}{1 - \bar \alpha_{t}} x_t\)
\(= \frac{\sqrt{\bar \alpha_{t-1}} \beta_{t}}{1 - \bar \alpha_{t}} (\frac{1}{\sqrt{\bar \alpha_{t}}}(x_t - \sqrt{1 - \bar \alpha_{t}} \epsilon_{t})) + \frac{\sqrt{\alpha_t} (1 - \bar \alpha_{t-1})}{1 - \bar \alpha_{t}} x_t\)
\(= \frac{\sqrt{\bar \alpha_{t-1}} (1 - \alpha_{t})}{1 - \bar \alpha_{t}} (\frac{1}{\sqrt{\bar \alpha_{t}}}(x_t - \sqrt{1 - \bar \alpha_{t}} \epsilon_{t})) + \frac{\sqrt{\alpha_t} (1 - \bar \alpha_{t-1})}{1 - \bar \alpha_{t}} x_t\)
\(= \frac{\sqrt{k} (1 - \alpha_{t})}{1 - \alpha_{t} k} (\frac{1}{\sqrt{\alpha_{t} k}}(x_t - \sqrt{1 - \alpha_{t} k} \epsilon_{t})) + \frac{\sqrt{\alpha_t} (1 - k)}{1 - \alpha_{t} k} x_t\)
by \(k = \bar \alpha_{t-1}\) 및 \(\alpha_{t}k = \bar \alpha_{t}\)로 치환
\(= \frac{1}{\sqrt{\alpha_{t}}} x_t - \frac{1 - \alpha_{t}}{\sqrt{\alpha_{t}}\sqrt{1 - \alpha_{t}k}} \epsilon_{t}\)
\(= \frac{1}{\sqrt{\alpha_{t}}} x_t - \frac{1 - \alpha_{t}}{\sqrt{\alpha_{t}}\sqrt{1 - \bar \alpha_{t}}} \epsilon_{t}\)
\(= \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{t})\)

• \(q(x_{t-1} | x_t, x_0)\) 결과 :
  \(q(x_{t-1} | x_t, x_0) = N(x_{t-1}; \tilde \mu_{t}(x_t), \tilde \beta_{t})\)
  where \(\tilde \mu_{t}(x_t) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{t})\)
  and \(\tilde \beta_{t} = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t}\)

Step 8. Obtain \(p_{\theta}(x_{t-1} \| x_t)\)

우리의 목적은
\(D_{KL}(q(x_{t-1} | x_t, x_0) \| p_{\theta}(x_{t-1} | x_t))\) 최소화
즉, \(p\)의 분포를 \(q\)의 분포에 approx.하는 것이다

\(q(x_{t-1} | x_t, x_0)\) 의 mean, variance 인
\(\tilde \mu_{t}(x_t) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{t})\)
\(\tilde \beta_{t} = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_{t}\) 에서
\(x_t, \alpha_{t}, \beta_{t}\)는 입력값 및 미리 정해놓는 상수값이라서
deep learning network인 \(\epsilon_{\theta}\) 가 시간 t에 따라 \(\epsilon_{t} \sim N(0, I)\) 을 학습하도록 하기 위해서
training param.로 학습할 수 있는 부분은 \(\epsilon_{t} \sim N(0, I)\) 뿐이다
즉, p와 q의 분포에서 차이가 날 수 있는 부분은 epsilon 뿐!

따라서 \(p_{\theta}(x_{t-1} | x_t)\)의 평균인 \(\mu_{\theta}(x_t, t)\) 는
\(\tilde \mu_{t}(x_t) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{t})\) 에서
\(\epsilon_{t}\) 만 \(\epsilon_{\theta}(x_t, t)\) 로 바꾼 값이다
\(\mu_{\theta}(x_t, t) = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{\theta}(x_t, t))\)

Step 9. Final DDPM Loss

Step 5.에 따르면 we have to minimize
\(E_{x_{1:T} \sim q(x_{1:T}|x_0)}[\frac{1}{2 \sigma_{t}^2} \| \tilde \mu_{t} (x_t, x_0) - \mu_{\theta} (x_t, t) \|^2] + C\)

\(E_{x_0, \epsilon}[\frac{1}{2 \|\Sigma(x_t, t) \|^2} \| \tilde \mu_{t} (x_t, x_0) - \mu_{\theta} (x_t, t) \|^2]\)
\(= E_{x_0, \epsilon}[\frac{1}{2 \|\Sigma \|^2} \| \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{t}) - \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{\theta}(x_t, t)) \|^2]\)
\(= E_{x_0, \epsilon}[\frac{(1 - \alpha_{t})^2}{2 \|\Sigma \|^2 \alpha_{t} (1 - \bar \alpha_{t})} \| \epsilon_{t} - \epsilon_{\theta}(x_t, t) \|^2]\)
\(= E_{x_0, \epsilon}[\frac{(1 - \alpha_{t})^2}{2 \|\Sigma \|^2 \alpha_{t} (1 - \bar \alpha_{t})} \| \epsilon_{t} - \epsilon_{\theta}(\sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1-\bar \alpha_{t}} \epsilon, t) \|^2]\)
since \(x_t = \sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1-\bar \alpha_{t}} \epsilon\)

앞의 weight term을 제거하면
최종 Loss 값은 드디어!!!
\(= E_{x_0, \epsilon}[\| \epsilon_{t} - \epsilon_{\theta}(\sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1-\bar \alpha_{t}} \epsilon, t) \|^2]\)
where \(x_t = q(x_t | x_0) = \sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1-\bar \alpha_{t}} \epsilon\) and \(\epsilon \sim N(0, I)\)

DDPM Pseudo-Code

• forward process : Training \(\epsilon_{\theta}\) for given input image \(x_0\)

while (converge){
  x_0 ~ q(x_0) # input image
  t ~ Uniform({1, ..., T}) # time step (integer)
  epsilon ~ N(0, I) # Gaussian target epsilon

  # gradient descent by DDPM loss
}

DDPM loss :
\(E_{x_0, \epsilon}[\| \epsilon_{t} - \epsilon_{\theta}(\sqrt{\bar \alpha_{t}} x_{0} + \sqrt{1-\bar \alpha_{t}} \epsilon, t) \|^2]\)

• backward process : Sampling from Gaussian noise img to new img by trained \(\epsilon_{\theta}\)

x_T ~ N(0, I) # start with Gaussian noise image

for (t = T, ..., 1){
  z ~ N(0, I) if t > 1 else z = 0  
  # sampling x_{t-1} from x_t by p_{theta}(x_{t-1} | x_t)
}

Sampling :
\(x_{t-1} = \frac{1}{\sqrt{\alpha_{t}}} (x_t - \frac{1 - \alpha_{t}}{\sqrt{1 - \bar \alpha_{t}}} \epsilon_{\theta}(x_t, t)) + \sigma_{t} z\)

Discussion

• Q1 :
  image prior \(q(X_t)\)를 모르기 때문에 \(q(X_{t-1} | X_t)\)를 계산할 수 없으므로 \(q(X_{t-1} | X_t)\)를 근사하는 \(p_{\theta}(X_{t-1} | X_t)\) 학습한다고 처음에 얘기했는데, 수식 유도를 보면 \(q(X_{t-1} | X_t, X_0)\) 의 분포를 알고 있지 않나?

• A1 :
  training dataset \(X_0\) 에 대한 \(q(X_{t-1} | X_t, X_0)\) 는 알 수 있다! (tractable)
  forward process에서 \(X_{t-1}\)에서 \(X_t\)로 더하는 noise 정보 (GT) 를 알고 있기 때문에 backward process에서의 \(q(X_{t-1} | X_t, X_0)\) 분포를 수식으로 구할 수 있다.
  이 때, 실제 분포 \(q(X_{t-1} | X_t, X_0)\)를 근사하는 \(p_{\theta}(X_{t-1} | X_t)\)를 학습한다면
  inference를 할 때에도 임의로 Gaussian sampling한 noise에 대해서도 \(p_{\theta}(X_{t-1} | X_t)\) 에 의해 image \(X_0\) 을 생성할 수 있다.
  수식 유도 과정을 보면 Step 2 에서 intractable \(q\) 를 계산 가능하도록 (tractable 하도록) 만들기 위해 \(q\) 분포의 조건부에 \(X_0\)을 추가하는 것을 확인할 수 있다.

• Q2 :
  diffusion model에서 Gaussian을 쓰는 이유

• A2 :
  Gaussian의 conditional도 Gaussian이듯 Gaussian이 tractable하기 때문!

출처 블로그 :
Diffusion Model
DDPM 수식 유도
DDPM 수식 유도
DDPM 코드 실습