DreamFusion (SDS loss)

Text-to-3D using 2D Diffusion (ICLR 2023)

DreamFusion: Text-to-3D using 2D Diffusion (ICLR 2023)

Ben Poole, Ajay Jain, Jonathan T. Barron, Ben Mildenhall

paper :
https://arxiv.org/abs/2209.14988
project website :
https://dreamfusion3d.github.io/
pytorch code :
https://github.com/ashawkey/stable-dreamfusion

Contribution

• SDS(Score Distillation) Loss 처음 제시
  • scalable, high-quality 2D diffusion model의 능력을 3D domain renderer로 distill
  • 3D 또는 multi-view training data 필요없고, pre-trained 2D diffusion model만 있으면, 3D synthesis 수행 가능!
  • DDPM은 denoising U-Net param.를 업데이트하여 \(x\) in pixel space를 업데이트하는 것이었는데,
    SDS loss는 U-Net을 freeze한 뒤 3D renderer (e.g. NeRF, 3DGS)로 만든 \(x = g(\theta)\) 를 거쳐 3D renderer param. \(\theta\) 를 업데이트

• NeRF가, Diffusion(Imagen) model with text에서 내놓을 만한 그럴 듯한 image를 합성하도록 함

• text-to-3D synthesis 발전 시작

Overview

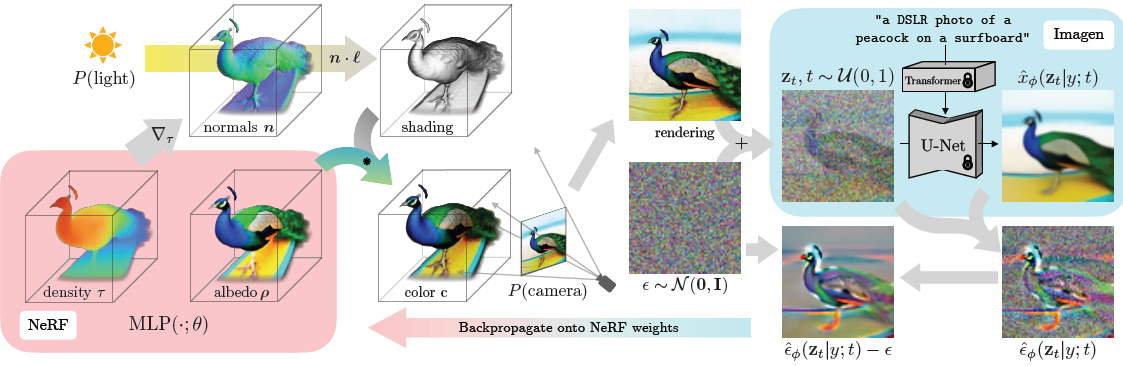
• Overview
  • initialize NeRF with random weight
  • for each iter.
    • camera 위치와 각도, light 위치와 색상을 randomly sampling
      \(P(camera), P(light)\)
    • NeRF로 image rendering
    • text embedding \(\tau\) 이용해서 NeRF param. \(\theta\) 에 대한 SDS loss 계산
    • update NeRF weight

Random camera, light sampling

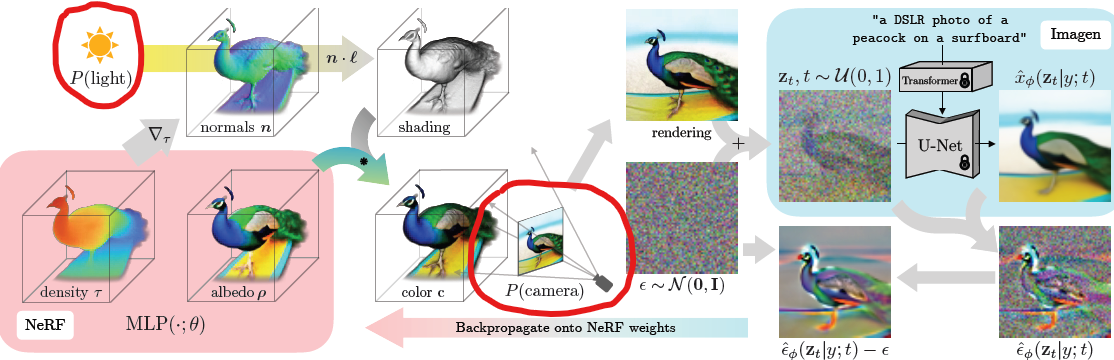
• camera :
  • 3D model을 bounded sphere 내부로 제한하고,
    spherical coordinate(구 표면)에서 camera 위치를 sampling하여
    구의 원점을 바라보도록 camera 각도 설정
  • width(64)에 0.7 ~ 1.35의 상수값을 곱하여 focal length 설정
• light :
  • camera 위치를 중심으로 한 확률분포로부터 light의 위치를 sampling하고
    (어떤 확률분포 ????)
    light 색상도 sampling

NeRF Rendering with shading

albedo : NeRF가 예측한 color

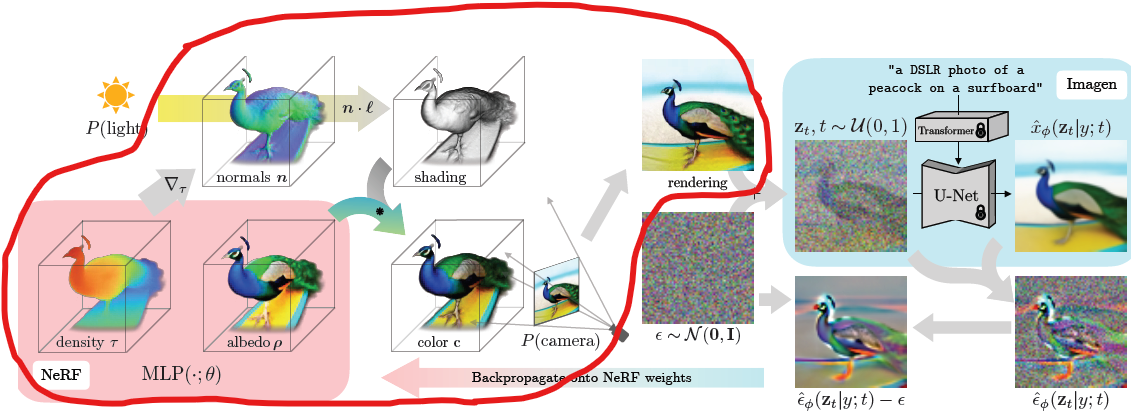
• rendering 방법 :
  1. albedo \(\rho\) 만으로 rendering
     (기존 NeRF와 동일)
  2. albedo \(\rho\) 뿐만 아니라 shading하여 rendering
  3. albedo \(\rho\) 를 white \((1, 1, 1)\) 로 바꾼 뒤 shading하여 rendering
• Shading의 역할 :
  • shading 없이 \(\rho\) 만으로 rendering하면
    평평한 3D model이 나와도 점수 높게 나옴
  • shading으로 (빛 반사에 따른) shape 정보까지 고려해서 rendering하면
    volume 있는 3D model이 되도록 촉구
• NeRF MLP \(\theta\) :
  • MLP output : volume density \(\tau\) 와 albedo \(\rho\)
• Normal \(n\) :
  \(n = - \frac{\nabla_{\mu} \tau}{\| \nabla_{\mu} \tau \|}\)
  where \(n\) 은 물체 표면의 법선벡터
  • normal vector의 방향은
    volume density \(\tau\) 가 가장 급격하게 변하는 방향, 즉 \(\nabla_{\mu} \tau\) 의
    반대 방향
• Shading \(s\) :
  \(s = (l_p \circ \text{max}(0, n \cdot \frac{l - \mu}{\| l - \mu \|})) + l_a\)
  where \(l_p\) 는 light 좌표 \(l\) 에서 나오는 light(광원) 색상
  where \(l_a\) 는 ambient light(환경 조명) 색상
  where \(\mu\) 는 shading 값을 계산할 surface 위 point 좌표
  where \(\circ\) 는 element-wise multiplication
  • \(n \cdot (l - \mu)\) 는 표면에서의 normal vector와 표면에서 광원까지의 vector 간의 내적이며,
    이는 Lambertian(diffuse) reflectance(난반사)에 의해 광원의 빛이 반사되는 정도를 나타냄
    왜냐하면, 빛이 표면에 수직으로 들어올수록 많이 반사됨
  • 만약 빛이 표면 반대쪽에 있어서 또는 back-facing normal로 잘못 예측해서
    내적 값 \(n \cdot (l - \mu)\) 이 음수일 경우
    난반사에 의해 광원의 빛이 반사되는 정도는 0
  • \(l_p \circ \text{난반사 정도} + l_a\) 에 의해
    광원의 색상 \(l_p\) 는 물체 표면의 난반사 정도에 따라 반영되고
    환경 조명의 색상 \(l_a\) 는 물체의 모든 표면에 일정하게 반영됨
• Color \(c\) :
  \(c = \rho \circ s\) 또는 \(c = \rho\)

Diffusion loss with conditioning

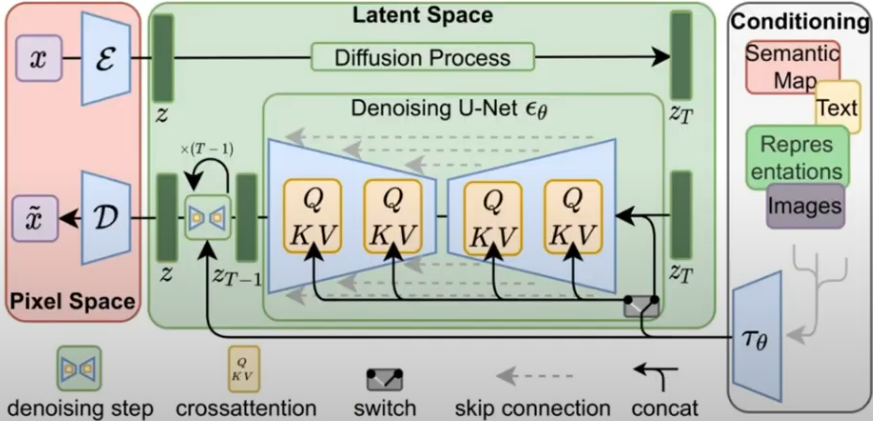
• Latent Diffusion model :
  • image \(x\) 가 아니라 encoder를 거친 image latent vector \(z\) 에 대해 noising, denoising 수행
  • noisy \(z_T\) 와 text embedding vector \(\tau_{\theta}\) 를 concat한 걸
    denoising하여 input image와 유사한 확률 분포를 갖도록 학습
    (text embedding vector \(\tau_{\theta}\) 을 conditioning (query) 로 넣어줌)

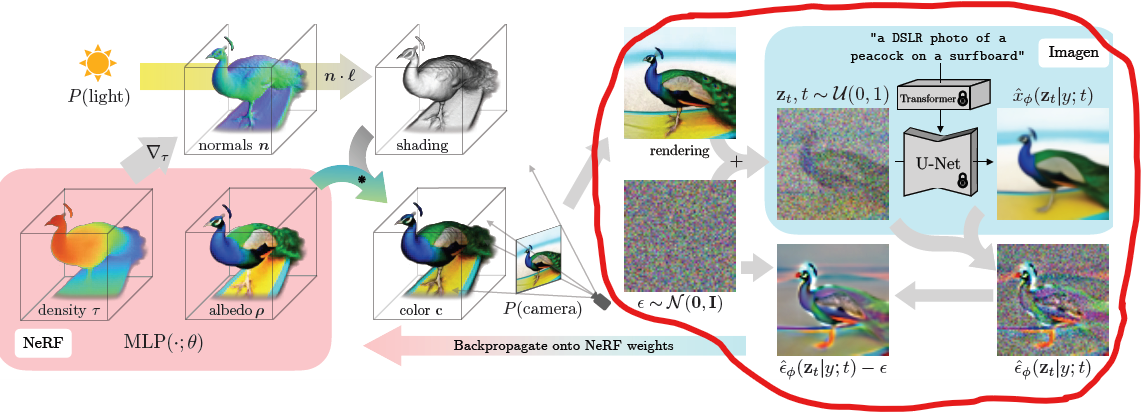
• text embedding vector \(\tau_{\theta}\) :
  T5-XXL text embedding을 거치기 전에
  text prompt engineering 수행
  • Elevation angle(고각)이 60도 이상일 때 “overhead view”
  • azimuth angle(방위각)에 따라 “front view”, “side view”, “back view”
  • text prompt engineering은 원래 좀 투박하게 하나?
• Imagen :
  • latent diffusion model with \(64 \times 64\) resolution
    (for fast training)

Sample in Parmater Space, not Pixel Space

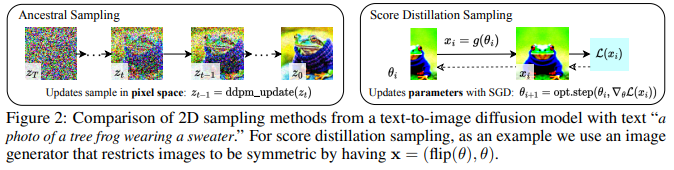
• \(x=g(\theta)\) : differentiable image parameterization (DIP)
  where \(x\) 는 image이고 \(g\) 는 renderer이고 \(\theta\) 는 renderer’s param.
  • more compact param. space \(\theta\) 에서 optimize ㄱㄴ
    (더 강력한 optimization algorithm 사용 ㄱㄴ)
• loss optimization으로 tractable sample 만들기 위해 diffusion model의 힘을 이용해서
  \(x\) in pixel space 가 아니라,
  \(x = g(\theta)\) 를 만든 \(\theta\) in parameter space 를 optimize
  s.t. \(x=g(\theta)\) 가 그럴 듯한 diffusion model sample처럼 보이도록

Optimization

• 실험적인 implementation :
  • noise level (time) sampling \(t\) :
    \(z_t, t \sim U[0, 1]\) 에서 noise level이 너무 크거나(\(t=1\)) 너무 작을 경우(\(t=0\)) instability 생기므로
    noise level \(t \sim U[0.02, 0.98]\) 로 sampling
  • guidance weight \(w\) :
    Imagen이 NeRF에 얼만큼 영향을 미칠지(guide할지)인데,
    high-quality 3D model을 학습하기 위해서는
    CFG(classifier-free guidance) weight \(w\) 를 큰 값(100)으로 설정
    • NeRF MLP output color가 sigmoid에 의해 [0, 1]로 bounded되어있으므로 constrained optimization 문제라서 guidance weight 커도 딱히 artifacts 없음
    • 작은 guidance weight 값을 사용할 경우
      Diffusion model로부터의 SDS loss의 mode-seeking property가 덜 반영되어
      sample들이 여러 mode를 부드럽게 연결하려는 경향을 가지므로
      오히려 생성된 image의 디테일이 떨어지는 over-smoothing 현상 발생!
      (큰 guidance weight 값을 사용하여 mode-seeking property를 많이 반영하여 sample들이 특정 mode에 강하게 집중되도록 하여 분명한 특징을 가진 image들이 생성되도록 해야 좋음!)
      • Diffusion model의 forward process의 mean-seeking property :
        • 원래 data distribution \(q(x_{0})\) 에 점점 더 강한 Gaussian noise를 추가하면서 data 개별적인 특징들이 점점 희미해지고 점점 perfect noise \(N(0, I)\) 를 향해 감
      • Diffusion model의 backward process의 mode-seeking property :
        • noise를 제거하면서 점점 원래의 data distribution \(q(x_{0})\) 로 복원하려 함
        • noise 제거 과정에서 Langevin Dynamics sampling 방법을 사용하는데, 이는 mode-seeking property 를 가지고 있음
          (원래 분포 \(q(x_{0})\) 의 뚜렷한 특징을 잘 복원하기 위해 sample들이 mode 지점에서 집중되어 sampling됨!)
  • seed :
    특히 noise level이 높을 때 density는 smoothed 되어 distinct modes를 많이 가지지 않고,
    SDS Loss는 mode-seeking property를 가지고 있으므로
    random seed 바꿔도 실험 결과는 큰 차이 없음
• implementation :
  • train : TPUv4, 15000 iter., 1.5h with Distributed Shampoo optimizer
  • rendering : 각 cpu는 개별 view를 rendering하는데 사용

Rendering

Structure

• Mip-NeRF 360 구조 사용
• entire scene 대신 single object를 generate할 때
  bounded sphere 내에서 NeRF view-synthesis 하면 빠르게 수렴 및 좋은 성능
• 보통 view-synthesis에서 배경을 검은색 또는 고정된 색으로 설정하기도 하는데,
  본 논문은 자연스러운 환경 조명(ambient light)을 반영하기 위해
  \(\gamma(d)\) 를 input으로 받아 별도의 MLP로 배경(environment map) 색상을 계산한 뒤 그 위에 ray rendering
  • 누적 \(\alpha\) (투명도) 값이 1인 경우 : 배경이 보이는 부분으로, 배경 색상을 그대로 사용
  • 누적 \(\alpha\) (투명도) 값이 0인 경우 : 물체가 배경을 가리는 부분으로, 물체 색상을 그대로 사용
  • 중간 값인 경우 : 배경(environment map) 색상과 물체(3DGS accumulate) 색상을 적절히 섞음

Geometry Regularizer

• DreamField의 regularization :
  • empty space가 불필요하게 채워지는 것을 방지
  • \(L_T = - \text{min} (\tau, \text{mean}(T(\theta, p)))\) :
    평균 transmittance가 클수록 loss가 작음
    where \(T(\theta, p)\) : transmittance with NeRF parameter \(\theta\) and camera pose \(p\)
    where \(\tau\) : 최대값 상수
• Ref-NeRF의 regularization :
  • normal vector \(n_i\) 의 back-facing (물체 안쪽을 향하는) 문제를 방지
  • orientation loss \(L = \Sigma_{i} w_i max(0, n_i \cdot d)^2\) :
    ray를 쏘면 물체의 앞면만 보이니까
    물체 표면의 normal vector 방향과 ray 방향의 내적이 음수여야 한다
    따라서 \(n_i\) 와 \(d\) 의 내적이 양수일 경우 back-facing normal vector이므로 penalize
    • textureless shading을 쓸 때 해당 regularization이 중요
      만약 해당 regularization 안 쓰면
      density field로 구한 normal 방향이 camera 반대쪽을 향하게 되어 shading이 더 어두워짐

SDS Loss

• NeRF로 rendering한 image \(x\) 에 noise를 더한 것을 \(z_t\) 로 두고
  U-Net \(\hat \epsilon_{\phi}(z_t | y, t)\) 을 빼서 denoising하여 얻은 image의 확률분포가
  2D diffusion prior가 내놓는 image의 확률분포와 비슷하도록 하는 loss이며,
  그 차이만큼 NeRF \(\theta\) 로 back-propagation

• 배경지식 :

  • DDPM Loss : \(E_{t, x_0, \epsilon} [\| \epsilon - \hat \epsilon_{\phi}(\alpha_{t}x_0 + \sigma_{t} \epsilon, t) \|^{2}]\)
    where \(\epsilon \sim N(0, I)\)
    where \(\alpha_{t} = \sqrt{\bar \alpha_{t}}\)
    where \(\sigma_{t} = \sqrt{1-\bar \alpha_{t}}\)
  • 만약 \(\theta\) 를 업데이트하기 위해 DDPM Loss를 직접 이용할 경우
    diffusion training의 multiscale 특성을 이용하고
    timestep schedule을 잘 선택한다면 [1] 잘 작동할 수 있다고 하지만
    실험해봤을 때 timestep schedule을 tune하기 어려웠고 DDPM Loss는 불안정했음
  • 위의 DDPM Loss는 denoising U-Net param.을 업데이트하기 위함이었고,
    우리는 fixed denoising U-Net을 이용하여
    NeRF param. \(\theta\) 업데이트하기 위한 SDS Loss를 새로 만들겠다!

Simple Derivation of SDS Loss

• DDPM Loss를 \(\phi\) 말고 \(\theta\) 에 대해 미분하고
  constant \(\frac{dz_t}{dx} = \alpha_{t} \boldsymbol I\) 를 \(w(t)\) 에 넣으면

x는 NeRF가 생성한 image이고, y는 text embedding vector

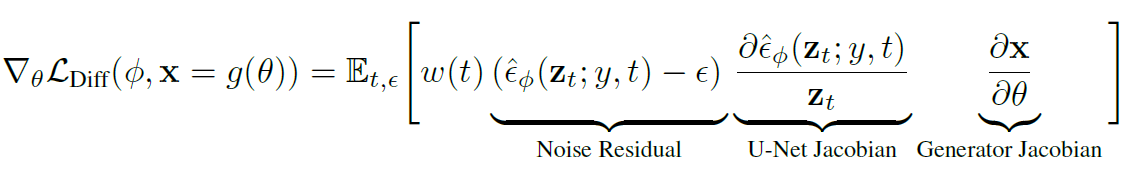
• 위의 U-Net Jacobian은 상당한 연산량을 가지는 데 비해
  작은 noise만 줄 뿐 큰 영향이 없으므로
  SDS Loss에서 U-Net Jacobian term은 생략

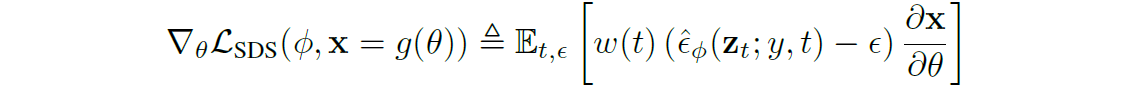
Derivation of SDS Loss

• SDS Loss gradient :
  • inspired by gradient of weighted probability density distillation loss [2]
  • \[\nabla_{\theta} L_{SDS}(\phi, x=g(\theta)) = \nabla_{\theta} E_{t, z_t|x}[w(t)\frac{\sigma_{t}}{\alpha_{t}}\text{KL}(q(z_t|g(\theta)) \| p_{\phi}(z_t | y, t))]\]
• KL-divergence :
  • Diffusion 의 KL-divergence 부분에 따르면
    모르는 분포 \(q(x)\) ( \(\epsilon\) ) 을 N개 sampling하여 trained \(p(x | \theta)\)로 근사하고자 할 때,
    \(KL(q \| p) \simeq \frac{1}{N} \sum_{n=1}^{N} {log q(x_n) - log p(x_n | \theta)}\) 이므로
    \(\text{KL}(q(z_t|g(\theta)) \| p_{\phi}(z_t | y, t)) = E_{\epsilon}[\text{log} q(z_t | x = g(\theta)) - \text{log} p_{\phi}(z_t | y)]\)
    \(\rightarrow\)
    \(\nabla_{\theta}\text{KL}(q(z_t|g(\theta)) \| p_{\phi}(z_t; y, t)) = E_{\epsilon}[\nabla_{\theta}\text{log} q(z_t | x = g(\theta)) - \nabla_{\theta}\text{log} p_{\phi}(z_t | y)]\)
• \(\theta\) 에 대한 \(\text{log}q\) 의 미분 :
  • gradient of forward process entropy w.r.t mean param. \(\theta\)
    (variance는 고정)
  • 아래 수식을 \(\nabla_{\theta}log q(z_t | x = g(\theta))\) 계산에 이용
    \(z_t = \alpha_{t} x + \sigma_{t} \epsilon \sim N(\alpha_{t} x, \sigma_{t}^2)\)
    \(\rightarrow \text{log} q(z_t|x=g(\theta)) = -\frac{1}{2\sigma_{t}^2} \| z_t - \alpha_{t} x \|^2 + \text{constant}\)
    \(\rightarrow \frac{d\text{log}q(z_t | x)}{dx} = \frac{\alpha_{t}}{\sigma_{t}^2}(z_t - \alpha_{t} x) = \frac{\alpha_{t}}{\sigma_{t}^2}\sigma_{t}\epsilon = \frac{\alpha_{t}}{\sigma_{t}}\epsilon\)
    and \(\frac{d\text{log}q(z_t | x)}{dz_t} = -\frac{1}{\sigma_{t}^2}(z_t - \alpha_{t} x) = -\frac{1}{\sigma_{t}^2}\sigma_{t}\epsilon = -\frac{1}{\sigma_{t}}\epsilon\)
    and \(\frac{dz_t}{dx} = \alpha_{t}\)
  • \(\nabla_{\theta}log q(z_t | x = g(\theta)) = (\frac{d\text{log}q(z_t | x)}{dx} + \frac{d\text{log}q(z_t | x)}{dz_t}\frac{dz_t}{dx})\frac{dx}{d\theta}\)
    \(= (\frac{\alpha_{t}}{\sigma_{t}}\epsilon - \frac{1}{\sigma_{t}}\epsilon \alpha_{t})\frac{dx}{d\theta}\)
    \(= 0\)
    (\(q\) 는 고정된 variance의 noise를 사용하므로 \(\theta\) 에 대한 entropy \(\text{log}q\) 의 미분 값은 0)
    • 위의 식에서 \(\frac{d\text{log}q(z_t | x)}{dx}\) :
      parameter score function
      gradient of log probability w.r.t parameter \(x\)
      (\(x\) 에 대한 \(\text{log}q\) 의 gradient 계산)
    • \(\frac{d\text{log}q(z_t | x)}{dz_t}\frac{dz_t}{dx}\) :
      path derivative
      gradient of log probability w.r.t sample \(z_t\)
      (\(q\) 를 따르는 sample \(z_t\) 를 통해 \(x\) 에 대한 \(\text{log}q\) 의 gradient 계산)
  • path derivative term은 냅두고
    parameter score function term을 제거하여
    \(\epsilon\) 항을 남길 경우
    SDS loss gradient에 \(\epsilon\) 항과 \(\hat \epsilon_{\phi}\) 항이 포함되는데,
    \(\epsilon\) 을 \(\hat \epsilon\) 의 control-variate 로 생각하면 [3] 처럼 variance를 줄일 수 있음!
    (자세한 건 바로 아래에서 설명!)
    (variance가 작으면 optimization이 빨라지고 더 나은 결과를 도출할 수 있음)
    • control-variates Wikipedia :
      • Monte Carlo 기법에서 사용되는 variance reduction technique
      • unknown quantity’s estimate의 error(variance)를 줄이기 위해,
        known quantity’s estimate의 error 정보를 사용
      • unknown \(\mu\) 의 estimate \(m\) 을 구하고 싶은 상황에서 (\(E[m] = \mu\)),
        known \(\tau = E[t]\) (\(t\) 는 \(m\) 의 control variate!)를 사용하여 만든
        \(m^{\ast} = m + c (t - \tau)\) 는 여전히 any \(c\) 에 대해 \(\mu\) 의 estimate 이고 (\(E[m^{\ast}] = E[m] + c (E[t] - \tau) = E[m] = \mu\)),
        새로 만든 \(m^{\ast}\) 는 기존의 \(m\) 보다 variance가 작음!
        수식 유도해보면 \(Var(m^{\ast}) = Var(m) + c^{2} Var(t) + 2c \text{Cov}(m, t) \ge Var(m^{\ast})|_{c^{\ast} = -\frac{Cov(m, t)}{Var(t)}} = Var(m) - \frac{Cov(m, t)^{2}}{Var(t)} = (1 - Corr(m, t)^{2}) Var(m)\) 까지 작아질 수 있음!
        where \(Corr(m, t) = \frac{Cov(m, t)}{\sqrt{Var(t)} \sqrt{Var(m)}}\)
      • 이를 SDS loss gradient term에 적용해보면,
        unknown estimate \(m = \hat \epsilon\) 을 구하고 싶은 상황에서,
        known estimate (constant) \(t = \epsilon\) 을 \(\hat \epsilon\) 의 control-variate로 둔 뒤
        \(m^{\ast} = \hat \epsilon + c (\epsilon - E[\epsilon]) = \hat \epsilon + c (\epsilon - 0) = \hat \epsilon - \epsilon\) term (SDS loss gradient에 들어 있는 항)은 variance가 줄어든 버전임! 맞나? ???
• \(\theta\) 에 대한 \(\text{log}p_{\phi}\) 의 미분 :
  • gradient of backward process entropy (denoising U-Net) w.r.t mean param. \(\theta\)
  • \(\frac{d\text{log}q(z_t | x)}{dz_t}\) 구했듯이 \(\epsilon\) 대신 \(\epsilon_{\phi}\) 넣으면
    \(\nabla_{z_t} \text{log}p_{\phi}(z_t | y) = \frac{d\text{log}p_{\phi}(z_t | y)}{dz_t} = -\frac{1}{\sigma_{t}}\hat \epsilon_{\phi}\)
    and \(\frac{dz_t}{dx} = \alpha_{t}\)
  • \[\nabla_{\theta}\text{log} p_{\phi}(z_t | y) = \nabla_{z_t} \text{log}p_{\phi}(z_t | y) \frac{dz_t}{dx} \frac{dx}{d\theta} = - \frac{\alpha_{t}}{\sigma_{t}} \hat \epsilon_{\phi}(z_t | y) \frac{dx}{d\theta}\]
• SDS Loss gradient Summary :
  • SDS Loss gradient :
    \(\nabla_{\theta} L_{SDS}(\phi, x=g(\theta)) = E_{t, z_t|x}[w(t)\frac{\sigma_{t}}{\alpha_{t}}\nabla_{\theta}\text{KL}(q(z_t|g(\theta)) \| p_{\phi}(z_t | y, t))]\)
    \(= E_{t, \epsilon}[w(t)\frac{\sigma_{t}}{\alpha_{t}}E_{\epsilon}[\nabla_{\theta}\text{log} q(z_t | x = g(\theta)) - \nabla_{\theta}\text{log} p_{\phi}(z_t | y)]]\)
    \(= E_{t, \epsilon}[w(t)\frac{\sigma_{t}}{\alpha_{t}} (-\frac{\alpha_{t}}{\sigma_{t}}\epsilon \frac{dx}{d\theta} + \frac{\alpha_{t}}{\sigma_{t}} \hat \epsilon_{\phi}(z_t | y) \frac{dx}{d\theta})]\)
    \(= E_{t, \epsilon}[w(t)(\hat \epsilon_{\phi}(z_t | y) - \epsilon)\frac{dx}{d\theta}]\)
  • \(\nabla_{\theta}log q(z_t | x = g(\theta))\) 의 path derivative term은 \(\epsilon\) 과 관련 있고!
    \(\nabla_{\theta}\text{log} p_{\phi}(z_t | y)\) 은 \(\epsilon\) 의 예측, 즉 \(\hat \epsilon_{\phi}\) 와 관련 있고!
    둘의 KL-divergence를 loss term으로 사용한다!
    (\(\epsilon\) 을 \(\hat \epsilon\) 의 control-variate로 생각하여 [3] 방식처럼 둘의 차이로 SDS Loss gradient 만들 수 있음!)
• Other Papers :
  • Graikos et al. (2022) [1] :
    \(KL(h(x) \| p_{\phi}(x|y))\) 로부터
    \(E_{\epsilon, t}[\| \epsilon - \hat \epsilon_{\theta}(z_t | y; t) \|^2] - \text{log} c(x, y)\) 를 유도해서 loss로 썼지만,
    SDS와 달리 error 제곱 꼴이라서 costly back-propagation
  • DDPM-PnP :
    auxiliary classifier \(c\) 를 썼지만,
    SDS에서는 CFG(classifier-free-guidance) 사용
    (별도의 classifier 및 image label 없이 image caption만 conditioning으로 넣어줘서 model 학습)
  • noise level :
    • 정확한 PDF를 모르는 implicit model에서는 entropy의 gradient를 직접 계산하기 어려우므로
      대신 score function approx.로 계산하는데,
      보통 single noise level 에서의 amortized score model [4] 을 사용하여 한 가지 고정된 noise level에서 score를 학습
      (control-variate 사용 안 함)
    • SDS에서는 multiple noise level을 사용함으로써
      다양한 scale에서의 score를 학습하여 entropy의 gradient의 variance가 줄어들고 더 안정적으로 optimize 가능
  • GAN-like amortized samplers :
    GAN-like amortized samplers 는 Stein discrepancy 최소화 [5] , [6] 로 학습하는데,
    이는 SDS loss의 score 차이와 비슷

Pseudo Code

params = generator.init() # NeRF param.
opt_state = optimizer.init(params) # optimizer
diffusion_model = diffusion.load_model() # Imagen diffusion model
for iter in iterations:
  t = random.uniform(0., 1.) # noise level (time step)
  alpha_t, sigma_t = diffusion_model.get_coeffs(t) # determine constant for noisy z_t's mean, std.
  eps = random.normal(img_shape) # gaussian noise (epsilon)
  x = generator(params, ...) # NeRF rendered image
  z_t = alpha_t * x + sigma_t * eps # noisy NeRF image
  epshat_t = diffusion_model.epshat(z_t, y, t) # denoising U-Net
  g = grad(weight(t) * dot(stopgradient[epshat_t - eps], x), params) # derivative of SDS loss; stopgradient since do not update diffusion model
  params, opt_state = optimizer.update(g, opt_state) # update NeRF param.
return params

Experiment

Metric

• CLIP R-Precision [7] :
  • rendered image의 text 일관성을 측정
    (rendered image가 주어졌을 때 CLIP이 오답 texts 중 적절한 text를 찾는 accuracy로 계산)
  • 기존 CLIP R-Precision은 geometry quality는 측정할 수 없으므로
    평평한 flat geometry에 대해서도 높은 점수가 나올 수 있음
  • textureless render의 R-Precision(Geo)도 추가로 측정!
• PSNR :
  zero-shot text-to-3D generation에서는
  text에 대한 3D Ground-Truth를 만들 수 없으므로
  GT를 필요로 하는 PSNR 같은 metric은 사용하지 못함

Result

Geo(metry)의 CLIP R-Precision 점수가 높다는 것은 평평한 3D model이 아니라 shape 정보까지 고려했다는 것!

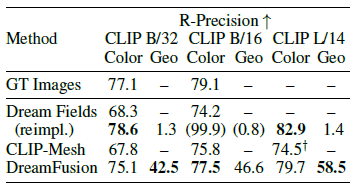
• 위의 표 설명 :
  • GT Images : oracle (CLIP training에 사용된 dataset)
  • CLIP-Mesh : CLIP으로 mesh를 optimize한 연구

• DreamFusion은 training할 때 Imagen을 썼고,
  Dream Fields와 CLIP-Mesh는 training할 때 CLIP을 썼으므로
  Dream Fields와 CLIP-Mesh를 사용하는 게
  DreamFusion보다 성능이 더 좋아야 하는데,
  위의 표를 보면 Color와 Geometry 평가에서 DreamFusion이 높은 성능(text 일관성)을 보인다는 것을 확인할 수 있다

• 아쉬운 점 :
  비슷한 다른 모델이 있다면 PSNR, SSIM 등으로 비교할 수 있었을텐데
  비교군이 없어서 R-Precision으로 consistency 측정만 했음

Ablation Study

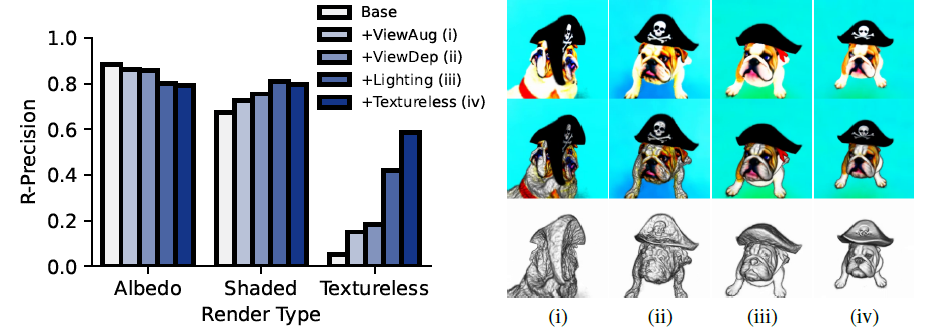
• 어떤 기법이 얼마나 성능에 기여했는지 파악하기 위해
  4가지 기법을 점진적으로 추가
  • (i) ViewAug : view-points의 범위를 넓힘
  • (ii) ViewDep : view-dependent text prompt-engineering 사용
    (e.g. “overhead view”, “side view”)
  • (iii) Lighting : 조명 사용
  • (iv) Textureless : albedo를 white로 만들어서 (color 없이) shading
• geometry quality를 확인하기 위해
  3가지 rendering 기법을 비교
  • (Top) Albedo : albedo \(\rho\) 만으로 rendering
    (기존 NeRF와 동일)
  • (Middle) Full Shaded : albedo \(\rho\) 뿐만 아니라 shading하여 rendering
  • (Bottom) Textureless : albedo \(\rho\) 를 white \((1, 1, 1)\) 로 바꾼 뒤 shading
• 결과 설명 :
  • 기법 추가 없이 Albedo rendering 하면 R-Precision은 높게 나오는데
    Geometry가 엄청 이상함 (e.g. 머리 2개 가진 개)
  • ViewDep, Lighting, Textureless 기법 사용해야 정확한 geometry까지 recon할 수 있음
  • (ii) ViewDep의 영향 :
    geometry 개선되지만, surface가 non-smooth하고 Shaded rendering 결과가 bad
  • (iii) Lighting의 영향 :
    geometry 개선되지만, 어두운 부분은 (e.g. 해적 모자) 여전히 non-smooth
  • (iv) Textureless의 영향 :
    geometry smooth하게 만드는 데 도움 되지만, color detail (e.g. 해골 뼈)이 geometry에 carved 되는 문제 발생

Limitation

• SDS를 적용하여 만든 2D image sample은 over-saturated 혹은 over-smoothed result
  • dynamic thresholding [8] 을 사용하면 SDS를 image에 적용할 때의 문제를 완화시킬 수 있다고 알려져 있긴 하지만, NeRF context에 대해서는 해결하지 못함
    (dynamic thresholding이 뭔지 아직 몰라서 읽어 봐야 됨 ???)
• SDS를 적용하여 만든 2D image sample은 diversity 부족
  (random seed 바꿔도 3D result에 큰 차이 없음)
  • reverse KL divergence의 mode-seeking property (for variational inference and prob. density distillation) 때문에
    특정 mode에 집중해서 sampling되는 경향이 있어서 seed를 바꾸더라도 2D image sample의 다양성 부족
• \(64 \times 64\) Imagen (low resol.)을 사용하여 3D model의 fine-detail이 부족할 수 있음
  • diffusion model 또는 NeRF를 더 큰 걸 사용하면 문제 해결할 수 있지만, 그만큼 겁나 느려지지…
• 2D image로부터 3D recon.하는 게 원래 어렵고 애매한 task임
  • inverse problem : 같은 2D images로부터 무수히 많은 3D worlds가 존재할 수 있으니까
  • local minima : optimization landscape가 highly non-convex하므로 local minima에 빠지지 않기 위한 기법들 필요
    (local minima : e.g. 모든 scene content가 하나의 flat surface에 painted된 경우)
  • more robust 3D prior가 도움 될 것임

Latest Papers

• 본 논문 DreamFusion과 관련된 논문들
  • ProlificDreamer
  • CLIP Goes 3D
  • Magic3D
  • Fantasia3D
  • CLIP-Forge
  • CLIP-NeRF
  • Text2Mesh
  • DDS (Delta Denoising Score)

Question

• Q1 : SDS loss로 image rendering한 samples의 경우 diversity가 부족하고 그 이유가 mode-seeking property라는 거 같은데,
  오히려 diversity가 부족한 게 단점이 아니라,
  mode-seeking property로 중요한 부분을 잘 캐치해서 consistent하게 그려내는 게 장점이 될 수 있지 않나요?

• A1 : TBD ???
  • Diffusion을 포함한 Generative Model에서 다양성 (diversity)는 매우 중요한 성질!
  • While modes of generative models in high dimensions are often far from typical samples (Nalisnick et al., 2018), the multiscale nature of diffusion model training may help to avoid these pathologies. ?????

• Q2 : \(\theta\) 에 대한 \(\text{log}q\) 의 미분에서 path derivative term은 냅두고 parameter score function term은 제거해서 control-variates 기법에 의해 variance를 줄였다고 하는데,
  parameter score function term을 걍 제거해버리는 게 좀 야매 아닌가요?

• A2 : TBD ???