MASt3R

Grounding Image Matching in 3D with MASt3R

Vincent Leroy, Yohann Cabon, Jérôme Revaud

paper :
https://arxiv.org/abs/2406.09756
project website :
https://europe.naverlabs.com/blog/mast3r-matching-and-stereo-3d-reconstruction/
code :
https://github.com/naver/mast3r
reference :
https://xoft.tistory.com/100

Contribution

DUSt3R :
- 많은 연산을 필요로 하는 SfM 생략 (pose-free)
- transformer 기반으로
  2D(img pixel)-to-3D(point map) mapping 예측하여
  regression-based 3D recon. 수행
- predicted pointmap 기반으로
  intrinsic/extrinsic camera param. 추정 가능
MASt3R :
- DUSt3R 후속 논문으로,
  DUSt3R을 활용하여 Image Matching에 특화시킴
  - Image Matching 문제를 3D 상에서 풂
  - quality 향상 및 속도 개선 및 많은 images 수 커버 가능

Image Matching

Image Matching 문제를 3D 상에서 풀기 때문에
2개 image의 공통 영역이 매우 적더라도 Image Matching 잘 수행 가능!
Image Matching 기법의 문제 및 해결 :
- 문제 1)
  전통적인 Image Matching은 keypoint을 추출하여 local-invariant descriptor로 변형한 뒤
  feature space에서 거리를 비교하여 Matching을 수행했음
  조명 변화와 시점 변화에도 정확했고 적은 keypoint 수로도 [ms] 단위로 Matching 가능했음
  하지만 geometry context는 고려하지 못했고
  반복 패턴이나 low-texture 영역에서는 잘 수행하지 못했음
- 해결 1)
  local descriptor 대신 global descriptor를 이용하는 SuperGlue(2020) 기법
- 문제 2)
  SuperGlue(2020)의 경우 keypoint descriptor가 충분히 encode되지 않으면 matching 도중에 global text를 활용할 수 없었음
- 해결 2)
  keypoint 대신 image 전체를 한 번에 matching하는 dense holistic matching 기법
  thanks to global attention
  e.g. LoFTR(2021) : 반복 패턴 및 low-texture 영역에 robust하고 dense correspondence 만들 수 있음
- 문제 3)
  LoFTR(2021)은 Map-free localization benchmark의 VCRE 평가에서 낮은 성능
  현실적으로 Image Matching task는 같은 3D point에 대응되는 pixel을 찾는 문제인데 지금까지 전통적인 matching 기법들은 전부 2D 상에서 이루어졌기 때문
- 해결 3)
  2D pixel - 3D point correspondence 다루는 DUSt3R 활용
- 문제 4)
  DUSt3R은 3D recon.을 목적으로 만들어졌기 때문에
  시점 변화에는 강인하지만 Image Matching에서는 비교적 부정확
- 해결 4)
  MASt3R(본 논문)에서는 DUSt3R을 Image Matching에 특화하는 방법에 대해 다룸!

DUSt3R Framework

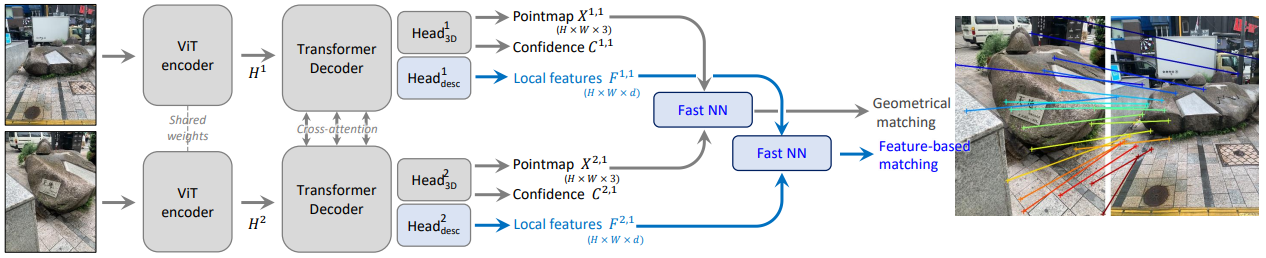
DUSt3R과 달라진 점 :
- DUSt3R에서는 3D recon.이 목적이었기 때문에
  view-point가 달라지더라도 같은 크기의 물체를 recon.해야 함
  즉, scale-invariant하도록 만들기 위해
  각 view-point에서 averaged depth 값으로 나누어 normalize해주었음
  \(\rightarrow\)
  MASt3R에서는 서로 다른 scale의 images인 상태에서 image matching task를 수행해야 하므로
  (scale을 고려해야 하므로)
  regression loss에서 scale(depth) normalization 파트를 없앰
Loss :
- regression loss :
  \(L_{regr} (v, i) = \| \frac{1}{z} X_{i}^{v, 1} - \frac{1}{\bar z} \bar X_{i}^{v, 1} \|\)
  - \(i\) : each point, \(v\) : each view
  - \(z = \bar z\) : averaged depth of GT point
- confidence loss :
  \(L_{conf} = \sum_{v \in \{ 1, 2 \}} \sum_{i \in D^{v}} C_{i}^{v, 1} L_{regr}(v, i) - \alpha \text{log} C_{i}^{v, 1}\)
  - \(C_{i}^{v, 1}\) : confidence score
    물체인 부분에서는 3D point를 비교적 정확히 예측할 수 있으므로 confidence가 높고,
    하늘 또는 반투명인 부분에서는 3D point를 정확하게 예측할 수 없으므로 confidence가 낮게 나옴
  - \(C_{i}^{v, 1} L_{regr}(v, i)\) :
    confidence가 큰 (확실한) point에서는 GT와의 regression loss \(L_{regr}\) 가 더 작도록
  - \(- \alpha \text{log} C_{i}^{v, 1}\) : regularization term
    confidence \(C_{i}^{v, 1}\) 값이 너무 작아지지 않도록
- matching loss (cross-entropy classification loss) :
  \(L_{match} = - \sum_{(i, j) \in \hat M} (\text{log} \frac{s_{\tau} (i, j)}{\sum_{k \in P^{1}} s_{\tau} (k, j)} + \text{log} \frac{s_{\tau} (i, j)}{\sum_{k \in P^{2}} s_{\tau} (i, k)})\)
  다음 section에서 언급할 예정
- total loss :
  \(L_{tot} = L_{conf} + \beta L_{match}\)

Matching Prediction Head

기존 DUSt3R의 Head output :
extreme한 view-point 변화에도 robust
- per-pixel Pointmap \(X_{i}^{v, 1} \in R^{H \times W \times 3}\)
- per-pixel Confidence score \(C_{i}^{v, 1} \in R^{H \times W}\)
MASt3R의 new Head output :
- per-pixel Local Feature \(D_{i}^{v} \in R^{H \times W \times d}\) (\(d = 24\))
Fast NN :
Fast Reciprocal Matching by Nearest Neighborhood
(다음 section에서 설명 예정)
- predicted Pointmap 이용하여 Geometrical matching 수행
  - 2개의 image에 대한 3D pointmap을 겹쳤을 때 align되도록
    3D 공간 상에서 pixel correspondence를 찾음
  - \(X^{2, k}\) 중에 3D point \(X_{i}^{1, k}\) 와 가장 가까운 3D point가 \(X_{j}^{2, k}\) 이고,
    동시에 \(X^{1, k}\) 중에 3D point \(X_{j}^{2, k}\) 와 가장 가까운 3D point가 \(X_{i}^{1, k}\) 일 때
    두 pixel \(i, j\) 사이에 correspondence 있다고 함
- predicted Local Feature 이용하여 Feature-based matching 수행
- 얘네들 어떻게 합치는지 ???
Loss :
- matching loss :
  constrastive learning에 사용되는 infoNCE Loss를 변형하여
  \(L_{match} = - \sum_{(i, j) \in \hat M} (\text{log} \frac{s_{\tau} (i, j)}{\sum_{k \in P^{1}} s_{\tau} (k, j)} + \text{log} \frac{s_{\tau} (i, j)}{\sum_{k \in P^{2}} s_{\tau} (i, k)})\)
  where \(s_{\tau} (i, j) = \text{exp}(- \tau D_{i}^{1 T} D_{j}^{2})\)
  근데 \(s_{\tau} (i, j)\) 는 similarity score이니까 \(\text{exp}\) 안에 - 가 없어야 할 것 같음! 오타인가? 아니면 내가 잘못 생각하고 있나?
  ?????
  - cross-entropy classification loss 꼴
    (regression loss 꼴 아님)
    \(\rightarrow\)
    정확히 correct pixel pair (positive sample) \((i, j)\) 에 대해서는 \(s_{\tau} (i, j)\) 이 높아지고
    nearby pixel (negative sample) \((i+1, j)\) 에 대해서는 \(s_{\tau} (i+1, j)\) 이 낮아지도록 설계하여
    nearby pixel로 regression하는 게 아니라 정확한 correct pixel pair를 분류하도록 하므로
    high-precision image matching 가능
  - positive sample :
    pixel correspondence가 있는 pixel pair (2개 image에서 모두 나타나고 3D point가 일치하는 pixel pair)
    1번 image의 \(i\)-th pixel이 2번 image의 \(j\)-th pixel과 correspondence 있다면
    \((i, j) \in \hat M = \{ (i, j) | \hat X_{i}^{1, 1} = \hat X_{j}^{2, 1} \}\)
    where \(X^{v, 1}\) : 1번 view-point를 중심좌표계로 두고 \(v\) 번 view에서 보이는 3D point 좌표
  - negative sample :
    positive sample들을 모은 뒤
    \(\hat M\) 에서 대응되지 않는 pixel pair
  - \(P^{1} = \{ i | (i, j) \in \hat M \}\) and \(P^{2} = \{ j | (i, j) \in \hat M \}\)
    따라서 log 안의 분자는 positive sample의 score에 해당하고
    log 안의 분모는 negative sample의 score에 해당

Fast Reciprocal Matching

그렇다면 위에서 positive sample \(M\) 은 어떻게 찾을까?

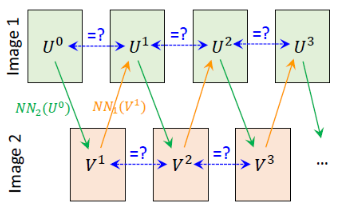
Fast Reciprocal Matching :
feature space \(D\) 에서 reciprocal matching 수행
- 기존 matching :
  Nearest Neighbor 기법 사용하여
  \(D^{1}\) 중에 \(D_{j}^{2}\) 와 가장 유사한 pixel이 \(D_{i}^{1}\) 이고,
  동시에 \(D^{2}\) 중에 \(D_{i}^{1}\) 와 가장 유사한 pixel이 \(D_{j}^{2}\) 일 때
  해당 \((i, j)\) pair에는 pixel correspondence가 있다고 함
  - complexity \(O(W^{2} H^{2})\)
- Fast Reciprocal matching :
  연산 줄이기 위해 image의 부분 pixel들로 matching 진행
  - Step 1)
    image 1 에서 \(k\) 개의 pixel을 uniform sampling하여 \(U^{0}\) 로 표기
  - Step 2)
    기존 matching 방법대로 Nearest Neighbor 기법 사용하여
    mapping from \(U^{0}\) to \(V^{1}\) 진행
    (\(V^{t+1}\) : image 2에서 \(U^{t}\) 와 가장 유사한 pixel들의 집합)
  - Step 3)
    기존 matching 방법대로 Nearest Neighbor 기법 사용하여
    다시 mapping from \(V^{1}\) to \(U^{1}\) 진행
    (\(U^{t+1}\) : image 1에서 \(V^{t+1}\) 와 가장 유사한 pixel들의 집합)
  - Step 4)
    만약 \(U^{t}\) 와 \(U^{t+1}\) 이 같다면 reciprocal pair로 저장
    \(M_{k}^{t} = \{ (i, j) | i \in U^{t+1}, j \in V^{t+1} \}\)
  - Step 5)
    또 다른 \(k\) 개의 pixel을 uniform sampling하여 Step 1) ~ Step 4)를 반복
    이 때, 이전 loop에서 matching된 \(U^{t}\) 는 빼서 계산하므로 (\(U^{t+1} = U^{t+1} \setminus U^{t}\))
    점점 un-converged point \(| U^{t} |\) 가 줄어들어 수렴
  - Step 6)
    최종적으로 reciprocal pair 집합 (positive sample) 만들 수 있음
    \(M_{k} = \cup_{t} M_{k}^{t}\)
  - complexity \(O(kWH)\)
    (모든 pixel 조합을 비교하지 않음)

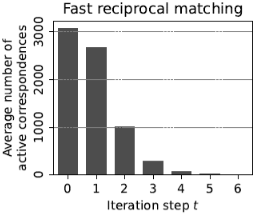
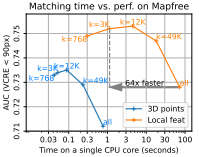
Coarse-to-Fine Matching

Coarse-to-Fine Matching :
연산 줄이기 위해
저해상도 image pair에서 Fast Reciprocal Matching 수행하여 집중해야 할 영역(window pair)을 찾고,
고해상도 window pair에서 Fine Matching 수행하여 fine pixel correpondence 얻음
low-resolution algorithm으로 high-resolution images를 match하기 위한 기법
- Step 1)
  \(k\) 배 subsampling하여 two downscaled images에서 Fast Reciprocal Matching 수행
  coarse pixel pair 집합을 \(M_{k}^{0}\) 으로 표기
- Step 2)
  원본 고해상도 image 위에 grid of overlapping window \(\in R^{w \times 4}\) 를 만든 뒤
  (each window crop measures 512 pixels in its largest dimension ?????)
  (인접한 windows overlap by 50%)
  coarse pixel pair \(M_{k}^{0}\) 를 가장 많이 포함하는 window pair \((w_{1}, w_{2}) \in W^{1} \times W^{2}\) 찾음
- Step 3)
  coarse pixel pair \(M_{k}^{0}\) 의 90%가 커버될 때까지
  greedy fashion으로 window pair를 추가
- Step 4)
  최종적으로 each window pair를 두 이미지로 보고,
  each window pair에 대해 각각 matching 수행하여 fine pixel pair 집합 구함
  Then they are finally mapped back to the original image coordinates and concatenated,
  thus providing dense full-resolution matching

Experiments

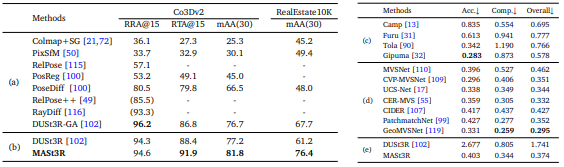
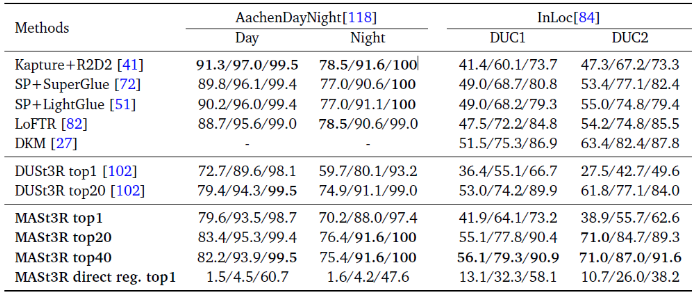
Map-free Localization

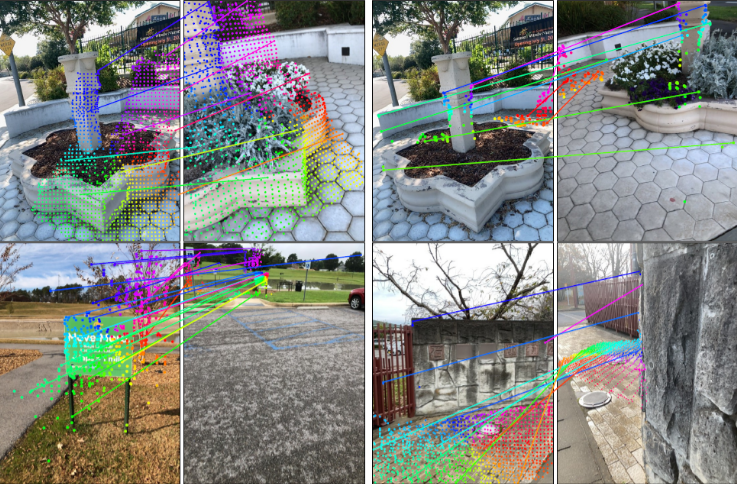
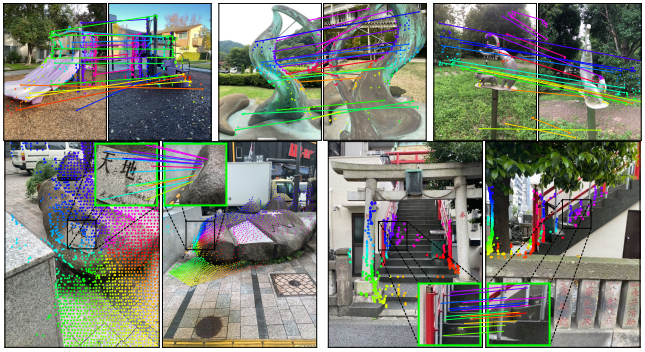
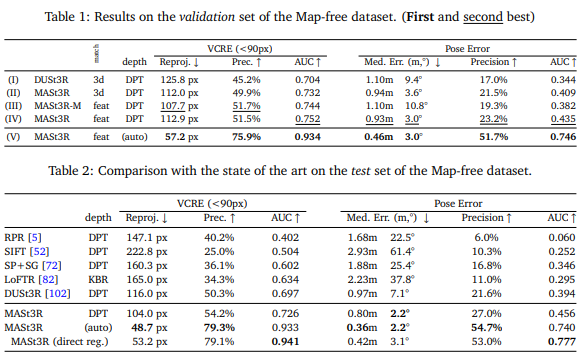
Multi-view Relative Pose Estimation

Visual Localization

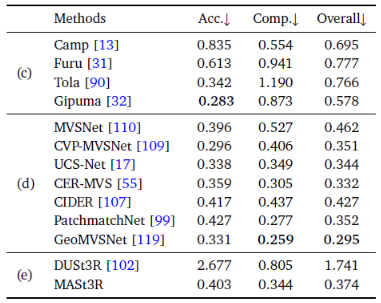
Multi-view 3D Reconstruction

Future Work

pose 없이 2D-to-3D 수행하는 DUSt3R, MASt3R에
3DGS를 적용한 NoPoSplat Link

Question

Q1 :
DUSt3R와 달리 MASt3R에서는 averaged depth 값으로 나누지 않는 이유를 다시 설명해주실 수 있을까요?
A1 :
- DUSt3R에서는 3D recon.이 목적이었기 때문에
  view-point가 달라지더라도 같은 크기의 물체를 recon.해야 함
  즉, scale-invariant하도록 만들기 위해
  각 view-point에서 averaged depth 값으로 나누어 normalize해주었음
- MASt3R에서는 서로 다른 scale의 images인 상태 그 자체에서 image matching task를 수행해야 하므로
  (scale을 고려해야 하므로)
  regression loss에서 scale(depth) normalization 파트를 없앰
Q2 :
3D 상에서 matching을 수행하므로 image 1에서 잘 보이는 부분이 image 2에서 잘 보이지 않더라도 잘 matching된다고 하셨는데,
왜 3D 상에서 matching을 수행한다고 하는지 이해가 되지 않습니다.
A2 :
Fast Reciprocal Matching 기법으로 두 가지 matching을 수행하는데,
- predicted 3D pointmap을 이용한 geometrical matching :
  2개의 image에 대한 3D pointmap을 겹쳤을 때 align되도록
  3D 공간 상에서 pixel correspondence를 찾음
  - \(X^{2, k}\) 중에 3D point \(X_{i}^{1, k}\) 와 가장 가까운 3D point가 \(X_{j}^{2, k}\) 이고,
    동시에 \(X^{1, k}\) 중에 3D point \(X_{j}^{2, k}\) 와 가장 가까운 3D point가 \(X_{i}^{1, k}\) 일 때
    두 pixel \(i, j\) 사이에 correspondence 있다고 함
- predicted local feature를 이용한 feature-based matching
Q3 :
geometrical matching 결과랑 feature-based matching 결과를 어떻게 합치나요?
A3 :
그 부분은 아직 살펴보지 못해서 코드를 한 번 봐야 알 수 있을 것 같습니다. 알아본 뒤 블로그 포스팅에 업데이트해놓도록 하겠습니다.
TBD ?????
Q4 :
\(U^{t} = U^{t+1}\) 이면 reciprocal pair로 저장하는데
만약 실패한 pixels가 많으면 결국 complexity가 \(O(kWH)\) 로 낮아지지 않을 것 같은데
complexity \(O(kWH)\) 가 어떻게 달성되나요?
A4 :
TBD ?????
Q5 :
Fast Reciprocal Matching에서 \(U^{t} \rightarrow V^{t+1}\) 와 \(V^{t+1} \rightarrow U^{t+1}\) 을 어떻게 정의하나요?
\(U^{t} \rightarrow V^{t+1}\) 는 Nearest Neighbor mapping이고 \(V^{t+1} \rightarrow U^{t+1}\) 는 transformer로 학습된 mapping 으로 진행하는 식인가요?
A5 :
아니요, \(U^{t} \rightarrow V^{t+1}\) 와 \(V^{t+1} \rightarrow U^{t+1}\) 둘 다 Nearest Neighbor mapping입니다.
\(D^{1}\) 중에 \(D_{j}^{2}\) 와 가장 유사한 pixel이 \(D_{i}^{1}\) 이고,
동시에 \(D^{2}\) 중에 \(D_{i}^{1}\) 와 가장 유사한 pixel이 \(D_{j}^{2}\) 일 때
해당 \((i, j)\) pair에는 pixel correspondence가 있다고 합니다.
즉, \(i\) 랑 가장 가까운 게 \(j\) 이더라도, \(j\) 랑 가장 가까운 게 \(i\) 가 아닐 수도 있다는 의미입니다.
따라서 \(i \in U^{t}\) 와 가장 가까운 게 \(j \in V^{t+1}\) 이고, \(j \in V^{t+1}\) 와 가장 가까운 게 \(i \in U^{t+1}\) 일 때 reciprocal pair로 저장(correspondence 존재)합니다.