MipNeRF

A Multiscale Representation for Anti-Aliasing Neural Radiance Fields

Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields

Jonathan T. Barron, Ben Mildenhall, Matthew Tancik, Peter Hedman, Ricardo Martin-Brualla, Pratul P. Srinivasan

paper :
https://arxiv.org/abs/2103.13415
project website :
https://jonbarron.info/mipnerf/
pytorch code :
https://github.com/bebeal/mipnerf-pytorch
https://github.com/google/mipnerf

핵심 요약 :

scale 잘 반영하도록 sample(region)을 pre-filtering!!

ray-tracing하여 point-encoding 대신
cone-tracing하여 region-encoding 이므로
frustum의 모양과 크기 정보를 encode할 수 있어서 scale 반영 가능

IPE 단계에서
high variance (구간 길이가 일정하다면 distant view)일 때
high freq.를 attenuate (pre-filtering) 하여
임의의 continuous-space scale을 가지는 scene에 대해 anti-aliased representation 학습 가능
\(\rightarrow\) multi-resolution dataset에 대해 성능 대폭 향상
\(\rightarrow\) scale-aware하므로 single MLP 하나만으로 충분하여 빠르고 가벼움

camera center로부터 각 pixel로 3D cone을 쏜 다음,
frustum을 multi-variate Gaussian으로 근사한 뒤,
Gaussian 내 좌표를 positional encoding한 것 (PE-basis-lifted Gaussian)에 대해
expected value \(E \left[ \gamma (x) \right]\) 계산
주의 : frustum이 Gaussian 분포를 따르는 게 아니라, frustum 내부의 mean, variance 값을 먼저 구한 뒤 해당 mean, variance 값을 갖는 Gaussian으로 frustum을 대신(근사)할 수 있다고 생각!

Introduction

기존 NeRF의 문제점 :
- rendering 위해 sampling할 때 single ray per pixel 쏴서 composite 하므로
  dataset에 있는 물체의 크기(resolution)가 일정하지 않을 때
  multi-scales images에 대해 학습하더라도
- blurry rendering in close-up views
  (because 가까이서 찍어서 zoom-out하면 물체 in high resolution)
- aliased(계단) rendering in distant views
  (because 멀리서 찍어서 zoom-in하면 물체 in low resolution)
- 그렇다고 multiple rays per pixel through its footprint로 brute-force super-sampling(offline rendering)하는 것은 정확하긴 하겠지만 too costly 비현실적
Minmap Approach :
classic 컴퓨터 그래픽스 분야에서 rendering할 때 aliasing을 없애기 위한 pre-filtering 기법
본 논문인 Mip-NeRF가 여기서 영감을 얻음
signal(e.g. image)을 diff. downsampling scales로 나타낸 뒤 pixel footprint를 근거로 ray에 사용하기 위한 적절한 scale을 고른다
render time에 할 복잡할 일을 pre-computation phase에 미리 하는 것일 뿐이긴 하지만, 주어진 texture마다 한 번만 minmap을 만들면 된다는 장점이 있다

Mip-NeRF :
- represent pre-filtered scene at continuous space of scales
- ray 대신 conical frustum 사용해서 anti-aliased rendering with fine details
- multi-scale variant of dataset에 대해 평균 error rate 60% 감소
- NeRF가 hierarchical sampling을 위해 coarse and fine MLP를 분리했다면, Mip-NeRF는 scale-aware하므로 single multi-scale MLP만으로 충분
  따라서 NeRF보다 7% 빠르고, param. 수는 절반이고, sampling도 더 효율적

ray 대신 cone을 쏘고, point-encoding 대신 frustum region-encoding

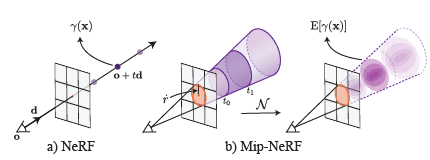
차이 : 기존 NeRF는 a single point를 encode하고, Mip-NeRF는 a region of space를 encode
기존 NeRF :
camera center로부터 각 pixel로 ray를 하나 쏜 다음 point sampling한 뒤 positional encoding
point-sampled feature는 ray가 보는 volume의 모양과 크기를 무시하는 것임
예를 들어 training할 때 camera1로부터 t 사이의 간격이 평균 10cm로 학습된 scene에 대해
camera2로 inference를 할 때 t 사이의 간격이 평균 1cm로 sampling된다면
10개의 점은 같은 point-based feature를 갖게 되어 scale을 고려하지 못함
이러한 ambiguity가 기존 NeRF의 성능 하락의 요인
Mip-NeRF :
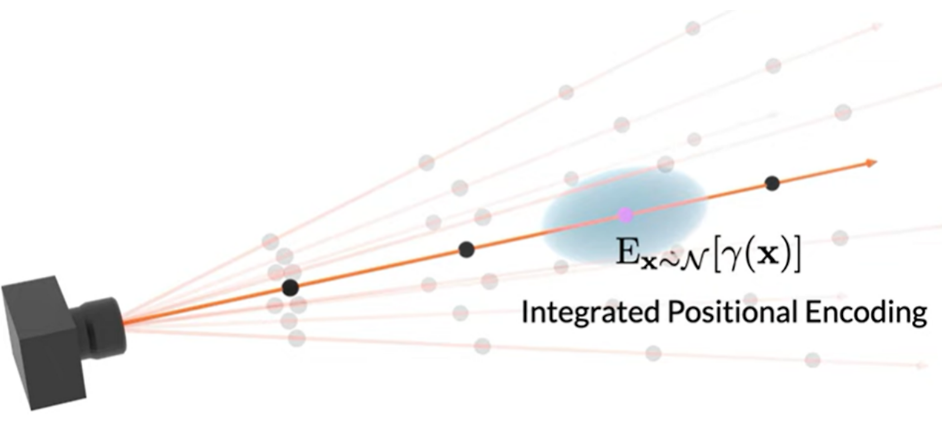
volume 정보를 반영하기 위해 camera center로부터 각 pixel로 3D cone을 쏜 다음, 3D point 및 그 주위의 Gaussian region을 encode하기 위해 IPE
IPE (integrated positional encoding) :
region을 encode하기 위한 방식
frustum을 multi-variate Gaussian으로 근사한 뒤,
Gaussian 내 좌표를 positional encoding한 것 (PE-basis-lifted Gaussian)에 대해 expected value \(E \left[ \gamma (x) \right]\) 계산

사진 출처 : https://xoft.tistory.com/16

Anti-aliasing in Rendering

anti-aliasing을 위한 고전적인 방법으로는 두 가지가 있다.

supersampling :
- rendering할 때 multiple rays per pixel을 쏴서 Nyquist frequency에 가깝게 sampling rate를 높임 (super-sampling)
- expensive as runtime increases linearly with the super-sampling rate, so used only in offline rendering
pre-filtering :
- target sampling rate에 맞춰서 Nyquist frequency를 줄이기 위해 scene에 lowpass-filter를 씌운 버전 사용
- scene을 미리 downsampling multi-scales (sparse voxel octree 또는 minmap)로 나타낸 뒤, ray 대신 cone을 추적하여 cone과 scene이 만나는 곳의 cone’s footprint에 대응되는 적절한 scale을 골라서 사용 (target sampling rate에 맞는 적절한 scale)
- scene에 filter 씌운 버전을 한 번만 미리 계산하면 되므로, better for real-time rendering

그런데 아래의 이유로 고전적인 multi-scale representation은 적용 불가능

input scene의 geometry를 미리 알 수 없으므로 pre-filtering 할 수가 없어서
대신 pre-filtering 방식 자체를 training할 때 학습해야 한다

input scene의 scale이 continuous하므로 a fixed number of scales (discrete)과 상황이 다르다

\(\rightarrow\) 결론 : 따라서 Mip-NeRF는 training하는 동안, 임의의 scale에 대해 query 받을 수 있는, scene의 pre-filtered representation을 학습한다.

Scene Representations for View Synthesis

만약 images of scene are captured densely 라면, novel view synthesis 위해, intermediate representation of scene을 reconstruct하지 않고 light field interpolation 기법 사용
만약 images of scene are captured sparsely 라면, novel view synthesis 위해, explicit representation of the scene’s 3D geometry and appearance를 reconstruct
- polygon-mesh-based representation (discrete, classic) :
  with either diffuse or view-dependent textures
  can be stored efficiently, but mesh geometry optimization에 gradient descent를 이용하는 것은 불연속점 및 극소점 때문에 어렵
- volumetric representation :
  - voxel-grid-based representation (discrete, classic) : deep learning으로 학습 가능, but 고해상도의 scene에는 부적합
  - coordinate-based neural representation (continuous, recent) : 3D 좌표를 그 위치에서의 scene의 특징(e.g. volume density, radiance)으로 mapping하는 continuous function을 MLP로 예측
    - implicit surface representation
    - implicit volumetric NeRF representation
문제점 :
그동안 view synthesis를 할 때 sampling 및 aliasing에는 덜 주목했다
\(\rightarrow\) classic discrete representation의 경우 앞에서 소개한 minmap, octree와 같은 고전적인 multi-scale pre-filtering 기법을 쓰면 aliasing 없이 rendering 가능하다
\(\rightarrow\) coordinate-based representation의 경우 scale이 continuous하므로 고전적인 anti-aliasing 기법은 사용할 수 없다
\(\rightarrow\) sparse voxel octree 기반의 multi-scale representation으로 implicit surface의 continuous neural representation을 구현한 논문 [1] 있긴 하지만, scene geometry의 priori를 알아야 한다는 제약이 있다
\(\rightarrow\) Mip-NeRF는 training하는 동안, 임의의 scale에 대해 query 받을 수 있는, scene의 anti-aliased (pre-filtered) representation을 학습한다.

Method

Cone Tracing and Positional Encoding

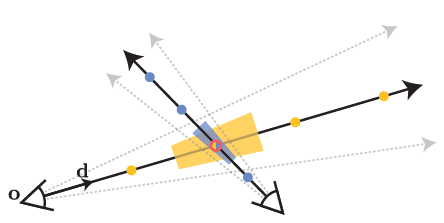
Cone Tracing :
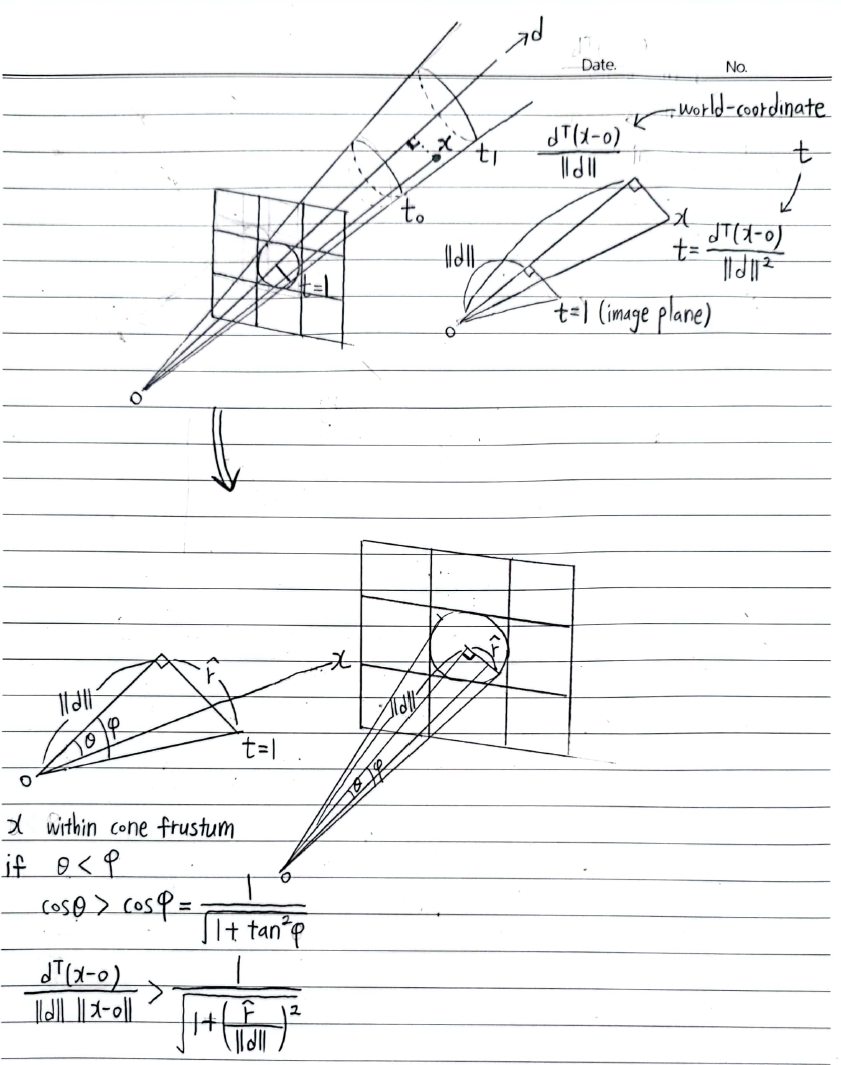
- Let \(d\) is cone direction vector from \(o\) to image plane
- Let \(\hat r =\) radius at image plane \(o + d\) \(= \frac{2}{\sqrt{12}}\) of pixel-width
  so that image plane에서의 cone의 \(x, y\) 축 variance가 pixel’s footprint의 variance와 같아지도록
  \(\hat r\)은 ray의 radius 변화율, 즉 frustum의 넓이를 결정
- \(t \in [t_0, t_1]\) 일 때 conical frustum 내의 \(x\)는 아래 범위의 값을 가질 때 indicator function \(F(x, o, d, \hat r, t_0, t_1)=1\)이다
  \(F(x, o, d, \hat r, t_0, t_1) = 1 \left\{ (t_0 \lt \frac{d^T(x-o)}{\| d \|^2} \lt t_1) \land (\frac{d^T(x-o)}{\| d \| \| x-o \|} \gt \frac{1}{\sqrt{1+(\frac{\hat r}{\| d \|})^2}}) \right\}\)

Region Encoding :
conical frustum 내에 있는 모든 좌표 \(x\)에 대해 직접
expected value \(E \left[ \gamma (x) \right] = \frac{\int \gamma (x) F(x, o, d, \hat r, t_0, t_1) dx}{\int F(x, o, d, \hat r, t_0, t_1) dx}\) 계산하면
region을 encode할 수 있는데
여기서 분자의 적분식은 closed-form solution이 없음
\(\rightarrow\) 직접 계산하지 말고
conical-frustum을 multi-variate Gaussian으로 근사한 뒤
Gaussian 내에 있는 모든 좌표 \(x\)에 대해
expected value \(E \left[ \gamma (x) \right]\) 계산
frustum을 multi-variate Gaussian으로 근사 :
- conical-frustum 단면은 대칭적인 원이기 때문에
  \(o, d\) 뿐만 아니라 아래의 3가지 정보만 알면 Gaussian을 특정할 수 있다
  - mean distance along ray from o \(\mu_{t}\)
  - variance along ray \(\sigma_{t}^2\)
  - variance perpendicular to ray \(\sigma_{r}^2\)
- Let mid-point \(t_{\mu} = \frac{t_0+t_1}{2}\)
  Let half-width \(t_{\sigma}=\frac{t_1-t_0}{2}\)
- 아래 수식의 유도과정은 하위에 별도로 정리함
  \(\mu_{t} = t_{\mu} + \frac{2t_{\mu}t_{\sigma}^2}{3t_{\mu}^2+t_{\sigma}^2}\)
  \(\sigma_{t}^2 = \frac{t_{\sigma}^2}{3} - \frac{4t_{\sigma}^4(12t_{\mu}^2-t_{\sigma}^2)}{15(3t_{\mu}^2+t_{\sigma}^2)^2}\)
  \(\sigma_{r}^2 = \hat r^2 (\frac{t_{\mu}^2}{4} + \frac{5t_{\sigma}^2}{12} - \frac{4t_{\sigma}^4}{15(3t_{\mu}^2+t_{\sigma}^2)})\)
- 위의 3가지 param.를 가지는 Gaussian은 t-coordinate에서 정의했는데
  아래 수식에 의해 world-coordinate으로 변환할 수 있다
  \(\mu = o + \mu_{t}d\)
  \(\Sigma = \sigma_{t}^2(dd^T) + \sigma_{r}^2(I-\frac{dd^T}{\| d \|^2})\)
  where \(dd^T =\) \(d\) 의 outer product은 \(d\) 방향으로의 투영을 의미하는 rank-1 matrix
  where \(I-\frac{dd^T}{\| d \|^2}\) 는 \(\frac{d}{\| d\ \|}\) 와 수직인 subspace로의 투영을 의미하는 rank-2 matrix
Integrated Positional Encoding (IPE) :
- 목표 : 위에서 계산한 \(\mu, \Sigma\) 의 Gaussian 내에 있는 모든 좌표 \(x\)에 대해 expected value \(E \left[ \gamma (x) \right]\) 계산
- 우선 PE (positional-encoding) basis P를 재정의
  \(P = \begin{pmatrix} \begin{matrix} 1 & 0 & 0 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 \\ 0 & 0 & 1 & 0 & 0 & 2\end{matrix} & \cdots & \begin{matrix} 2^{L-1} & 0 & 0 \\ 0 & 2^{L-1} & 0 \\ 0 & 0 & 2^{L-1}\end{matrix} \end{pmatrix}^T\)
  \(\gamma (x) = \begin{bmatrix} sin(Px) \\ cos(Px) \end{bmatrix}\)
- \(E \left[ \gamma (x) \right]\) 는 expectation over \(\gamma (x) = \begin{bmatrix} sin(Px) \\ cos(Px) \end{bmatrix}\) 이므로
  \(x\) in Gaussian of \(\mu, \Sigma\) \(\rightarrow\) \(\gamma (x)\) in Gaussian of \(\mu_{r}, \Sigma_{r}\) 로 변환해야 한다
  즉, PE basis P로 lift한 뒤의 mean과 covariance를 구해야 한다
  Since \(Cov[Ax, By] = A Cov[x, y] B^T\),
  \(\mu_{r} = P \mu\)
  \(\Sigma_{r} = P \Sigma P^T\)
- 최종적으로 \(E \left[ \gamma (x) \right]\) , 즉 expectation over lifted multi-variate Gaussian of \(\mu_{r}, \Sigma_{r}\) 을 구하면 된다
  Since \(E_{k \sim N(\mu, \sigma^2)}[e^{itk}] = exp(i \mu t - \frac{1}{2} \sigma^2 t^2)\) and \(sin(k) = \frac{e^{ik}-e^{-ik}}{2i}\) and \(cos(k) = \frac{e^{ik}+e^{-ik}}{2}\),
  \(E_{k \sim N(\mu, \sigma^2)}[sin(k)] = sin(\mu)exp(-\frac{1}{2}\sigma^2)\) and \(E_{k \sim N(\mu, \sigma^2)}[cos(k)] = cos(\mu)exp(-\frac{1}{2}\sigma^2)\) for each axis-k
  (positional-encoding은 각 dim.을 independently encode하므로 marginal distribution of \(\gamma (x)\) 에 의존)
  \(\rightarrow\)
  \(\gamma (\mu, \Sigma) = E_{x \sim N(\mu, \Sigma)} [\gamma (x)] = E_{Px \sim N(\mu_{r}, \Sigma_{r})} [\begin{bmatrix} sin(Px) \\ cos(Px) \end{bmatrix}]\)
  \(= \begin{bmatrix} sin(\mu_{r}) \circledast exp(-\frac{1}{2}diag(\Sigma_{r})) \\ cos(\mu_{r}) \circledast exp(-\frac{1}{2}diag(\Sigma_{r})) \end{bmatrix}\)
  where \(\circledast\) is element-wise multiplication
- \(diag(\Sigma_{r})\) 만 필요하므로 \(\Sigma_{r}\) 전부 계산하지 말고 efficiently diagonal만 계산
  PE-basis \(P\) 가 identity matrix이므로 \(diag(\Sigma)\) 만 필요
  \(diag(\Sigma_{r}) = diag(P \Sigma P^T) = \left[ diag(\Sigma), 4 diag(\Sigma), \ldots , 4^{L-1}diag(\Sigma) \right]^T\)
  where 3d-vector \(diag(\Sigma) = \sigma_{t}^2(d \circledast d) + \sigma_{r}^2(1-\frac{d \circledast d}{\| d \|^2})\)
  diagonal만 직접 계산하면, IPE feature는 PE feature랑 비슷하게 cost 소모

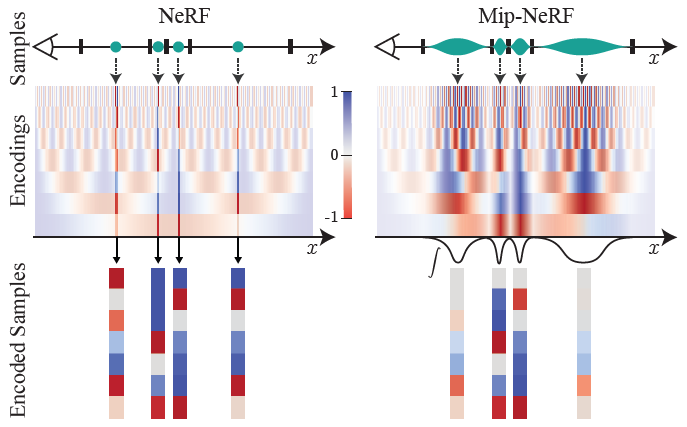
IPE vs PE :
- PE :
  point를 encode
  0~L까지의 모든 frequencies에 대해 동일하게 encode
  \(\rightarrow\) high-freq. PE features are aliased
  (PE period가 interval width보다 작은 경우 PE over interval oscillates repeatedly)
- IPE :
  interval region을 integrate하여 encode
  IPE feature를 만드는 데 사용된 interval \(t \in [t_0, t_1]\) width보다 period가 작은 high freq.의 경우 attenuate하여 anti-aliasing
  by \(exp(-\frac{1}{2}(\omega \sigma)^2)\) term
- 위와 같은 특성 덕분에 IPE는 interval 내 공간의 모양과 크기를 smoothly encode할 수 있는 anti-aliased PE 기법이다!
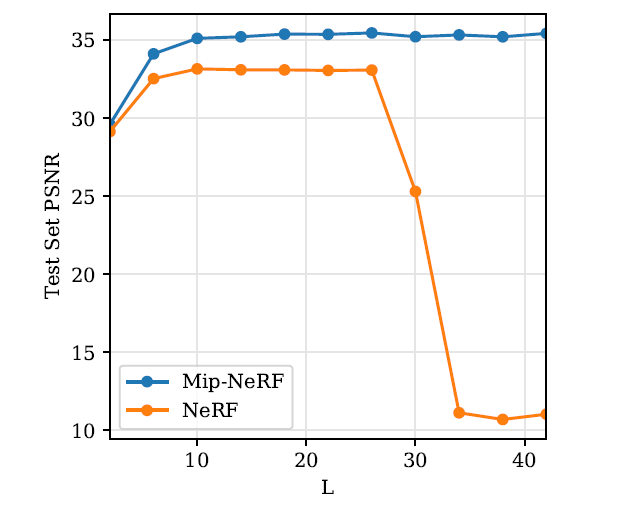
- high freq.는 IPE 단계 자체에서 attenuate되므로 L을 hyper-param.로 두지 않고 extremely large fixed-value로 두면 된다
  본 논문에서는 IPE feature의 last dim.이 numerical epsilon보다 작아지는 값인 \(L=16\) 으로 둠

NeRF에서는 L이 너무 크면 overfitting, Mip-NeRF에서는 IPE 단계 자체에서 high freq.를 attenuate하므로 L 커도 상관 없음

IPE의 의미 :
이게 Mip-NeRF의 핵심!!
- 수식 :
  PE-basis P 는 다양한 frequency \(\omega\) 로 구성되어 있고
  각 element는 \(E_{x \sim N(\mu, \Sigma)} [\gamma_{\omega} (x)] = sin(\omega \mu) exp(-\frac{1}{2}(\omega \sigma)^2)\)
- distant view :
  distant views (low-resolution), 즉 멀리 있는 wide frustum (high variance \(\sigma\))의 경우에는
  detail-info. (high freq. \(\omega\))는 training에 사용하지 않겠다
  \(\rightarrow\) more attenuation for high \(\sigma\) and high \(\omega\)
- close view :
  close views (high-resolution), 즉 가까이 있는 narrow frustum (low variance \(\sigma\))의 경우에는
  detail-info. (high freq. \(\omega\))를 training할 때 좀 더 허용
- 위와 같이 scale을 반영할 수 있으므로 blurry 및 aliased rendering 문제 해결 가능!
수식 Summary :
- frustum을 근사하는 multi-variate Gaussian의 mean, variance \(\mu, \sigma\) 를 구한다
- PE-basis P로 lift한 Gaussian의 mean, variance \(\mu_{r}, \Sigma_{r}\) 를 구한다
  \(P = \begin{pmatrix} \begin{matrix} 1 & 0 & 0 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 \\ 0 & 0 & 1 & 0 & 0 & 2\end{matrix} & \cdots & \begin{matrix} 2^{L-1} & 0 & 0 \\ 0 & 2^{L-1} & 0 \\ 0 & 0 & 2^{L-1}\end{matrix} \end{pmatrix}^T\)
  \(\gamma (x) = \begin{bmatrix} sin(Px) \\ cos(Px) \end{bmatrix}\)
  \(\mu_{r} = P \mu\) and \(\Sigma_{r} = P \Sigma P^T\)
- \(E_{x \sim N(\mu_{r}, \Sigma_{r})} [\gamma (x)] = \begin{bmatrix} sin(\mu_{r}) \circledast exp(-\frac{1}{2}diag(\Sigma_{r})) \\ cos(\mu_{r}) \circledast exp(-\frac{1}{2}diag(\Sigma_{r})) \end{bmatrix}\)
  (efficiently \(\Sigma_{r}\) 의 diagonal만 직접 계산)
  \(diag(\Sigma_{r}) = diag(P \Sigma P^T) = \left[ diag(\Sigma), 4 diag(\Sigma), \ldots , 4^{L-1}diag(\Sigma) \right]^T\)

Conical Frustum Integral Derivation

우선 Cartesian-coordinate에서 conical-coordinate으로 변환
\((x, y, z) = \varphi (r, t, \theta) = t \cdot (r cos \theta , r sin \theta , 1)\)
where \(\theta \in [0, 2 \pi)\) and \(t \geq 0\) and \(\| r \| \leq \hat r\)
Then,
\(dx dy dz = | det(D \varphi) | dr dt d\theta\)
\(= \begin{vmatrix} t cos\theta & t sin\theta & 0 \\ r cos\theta & r sin\theta & 1 \\ - rt sin\theta & rt cos\theta & 0 \end{vmatrix} dr dt d\theta\)
\(= (rt^2cos^2\theta + rt^2sin\theta) dr dt d\theta\)
\(= rt^2 dr dt d\theta\)
conical frustum의 volume \(V = \int \int \int dx dy dz = \int_{0}^{2\pi} \int_{t_0}^{t_1} \int_{0}^{\hat r} r t^2 dr dt d\theta = \pi \hat r^2 \frac{t_1^3 - t_0^3}{3}\) 에 대해
conical frustum에서 uniformly-sampling한 points의 probability density function은 \(\frac{rt^2}{V}\) 이다
t-axis :
- \[E \left[ t \right] = \int_{0}^{2\pi} \int_{t_0}^{t_1} \int_{0}^{\hat r} t \cdot \frac{rt^2}{V} dr dt d\theta = \frac{3(t_1^4 - t_0^4)}{4(t_1^3 - t_0^3)}\]
- \[E \left[ t^2 \right] = \int_{0}^{2\pi} \int_{t_0}^{t_1} \int_{0}^{\hat r} t^2 \cdot \frac{rt^2}{V} dr dt d\theta = \frac{3(t_1^5- t_0^5)}{5(t_1^3 - t_0^3)}\]
x-axis (\(x = t r cos \theta\)) :
- \[E \left[ t r cos\theta \right] = \int_{0}^{2\pi} \int_{t_0}^{t_1} \int_{0}^{\hat r} t r cos\theta \cdot \frac{rt^2}{V} dr dt d\theta = 0\]
- \[E \left[ (t r cos \theta)^2 \right] = \int_{0}^{2\pi} \int_{t_0}^{t_1} \int_{0}^{\hat r} t^2 r^2 cos^2 \theta \cdot \frac{rt^2}{V} dr dt d\theta = \frac{\hat r^2}{4} \frac{3(t_1^5 - t_0^5)}{5(t_1^3 - t_0^3)}\]
y-axis (\(y = t r sin \theta\)) :
conical frustum은 x, y에 대해 symmetric하므로 위에서 구한 x-axis에서의 값과 동일
이제 conical frustum 내부에 있는 random point에 대한 mean, covariance 값을 구할 수 있다
- mean distance along ray from o :
  \(\mu_{t} = E \left[ t \right] = \frac{3(t_1^4 - t_0^4)}{4(t_1^3 - t_0^3)}\)
- variance along ray :
  \(\sigma_{t}^2 = E \left[ t^2 \right] - (E \left[ t \right])^2 = \frac{3(t_1^5- t_0^5)}{5(t_1^3 - t_0^3)} - \mu_{t}^2\)
- variance perpendicular to ray :
  \(\sigma_{r}^2 = E \left[ x^2 \right] - (E \left[ x \right])^2 = \hat r^2 \frac{3(t_1^5 - t_0^5)}{20(t_1^3 - t_0^3)}\)
그런데 \(t_0, t_1\) 이 서로 가까우면 \(\frac{(t_1^5- t_0^5)}{(t_1^3 - t_0^3)}\) 과 같은 꼴은 numerically unstable as 0 or NaN instead of accurate values 이므로 training fail
\(\rightarrow\)
\(t_{\mu} = \frac{t_0+t_1}{2}\) and \(t_{\sigma}=\frac{t_1-t_0}{2}\) 로 re-parameterize하면
first-order term + correct(higher-order) term 꼴로 정리 가능하고
\(t_{\sigma}\) 가 작을 때에도 stable and accurate values 가짐
- \[\mu_{t} = t_{\mu} + \frac{2t_{\mu}t_{\sigma}^2}{3t_{\mu}^2+t_{\sigma}^2}\]
- \[\sigma_{t}^2 = \frac{t_{\sigma}^2}{3} - \frac{4t_{\sigma}^4(12t_{\mu}^2-t_{\sigma}^2)}{15(3t_{\mu}^2+t_{\sigma}^2)^2}\]
- \[\sigma_{r}^2 = \hat r^2 (\frac{t_{\mu}^2}{4} + \frac{5t_{\sigma}^2}{12} - \frac{4t_{\sigma}^4}{15(3t_{\mu}^2+t_{\sigma}^2)})\]
limitation :
frustum의 base 반지름과 top 반지름 차이가 클수록
conical-frustum을 multi-variate Gaussian으로 approx.하는 건 inaccurate
(예를 들어, camera FOV가 클 때 camera center와 매우 가까운 frustum)
대부분의 dataset에서는 흔하지 않은 case이긴 하지만,
macro photography with fisheye lens와 같은 특별한 case에서 MipNeRF를 쓸 때는 frustum을 multi-variate Gaussian으로 approx.하는 게 문제가 될 수 있음

Architecture

아래 내용들을 제외하고는 NeRF의 Architecture와 동일
- ray-tracing 대신 cone-tracing
- PE 대신 IPE
- point-encoding 이므로 \(n\)개의 구간에 대해 \(n\)개의 point sampling
  \(\rightarrow\)
  interval(region)-encoding 이므로 \(n\)개의 구간을 위해 \(n+1\)개의 point sampling
- PE feature로는 scale을 반영할 수 없으므로 두 가지 MLP (coarse-MLP, fine-MLP) 이용해서 hierarchical sampling
  (coarse-MLP에서는 \(N_c=64\) points per ray, fine-MLP에서는 \(N_c+N_f=64+128\) points per ray)
  \(\rightarrow\)
  IPE feature 자체가 scale을 반영할 수 있으므로 MLP 하나를 반복해서 써서 hierarchical sampling
  (한 번은 \(N_c=128\) points per ray, 그 다음은 \(N_f=128\) points per ray)
  NeRF와 MipNeRF의 공정한 비교를 위해 같은 수(총 256개)의 point를 사용
- hierarchical sampling에서 piecewise-constant PDF of normalized \(w\) 에 따라 fine-sampling 하기 전에
  weight \(w_k\) 를 바로 사용하지 않고
  2-tap MaxBlur filter 를 적용하여 weight의 wide and smooth upper bound 를 사용
  \(w_k^{\ast} = \frac{1}{2}(max(w_{k-1}, w_k) + max(w_k, w_{k+1})) + \alpha\)
  where 빈 공간에서도 일부 samples 추출되도록 보장하기 위해 \(\alpha=0.01\) 설정

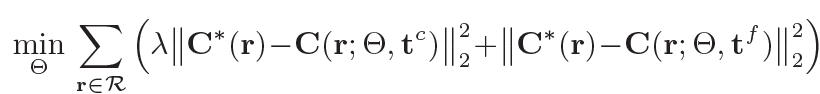
single MLP 쓰니까 coarse loss와 fine loss 간의 balance 맞추기 위해 hyperparam. gamma = 0.1로 설정

MaxBlur filter :
- MaxPool 대신 MaxBlurPool 쓰면 aliasing 감소 효과
- MipNeRF에서 weight에 MaxBlur filter 쓰는 이유 :
  scene content는 아무래도 연속적으로 존재하니까
  인접한 samples 간의 weight \(w\) 가 갑작스럽게 변하거나 불연속적인 outlier 를 제외하여 smoothing 해주는 역할

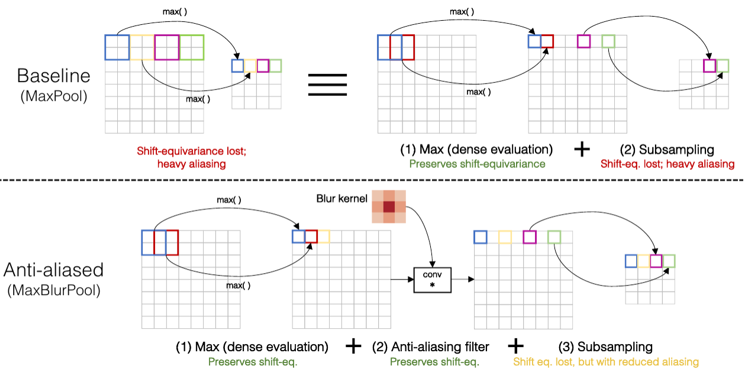
MaxBlur on sample weight / plot reference : https://charlieppark.kr/

Setting :
implementation on JaxNeRF
1 million iter., Adam optimizer, batch_size = 4096, lr from \(5 \cdot 10^{-4}\) to \(5 \cdot 10^{-6}\)

Result

multi-scale dataset에 대해 NeRF보다 error rate 60% 감소
single-scale dataset에 대해 NeRF보다 error rate 17% 감소
NeRF의 param.의 절반이고, NeRF보다 7% 빠름
brute-force super-sampling한 버전보다 22배 빠른데 accuracy 비슷

Question

Q&A reference : 3DGS online study
Q1 : distant view (scene content in low-resolution)일 때 IPE의 \(exp(-\frac{1}{2}(\omega \sigma)^2)\) term에 의해 high freq.를 attenuate하여 anti-aliasing 가능한 건 이해했는데,
close view (scene content in high-resolution)일 때 blurry rendering은 어떻게 해결??
A1 : 위에서 “Method - Cone Tracing and Positional Encoding - IPE의 의미”에 설명해둠
Q2 : image plane에서의 cone의 \(x, y\) 축 variance가 pixel’s footprint의 variance와 같아지도록
\(\hat r =\) radius at image plane \(o + d\) \(= \frac{2}{\sqrt{12}}\) of pixel-width 로 설정한다는데 이 부분이 이해가 되지 않습니다
A2 : uniform distribution을 가정했을 때 pixel의 square variance는 \(\frac{w^2}{12}\) 이고, cone at image plane의 circle variance는 \(\frac{\hat r^2}{4}\) 이므로 variance 값이 같으려면 \(\hat r = \frac{2}{\sqrt{12}} \times w\)
Q3 : \(E \left[ \gamma (x) \right] = \frac{\int \gamma (x) F(x, o, d, \hat r, t_0, t_1) dx}{\int F(x, o, d, \hat r, t_0, t_1) dx}\) 에서 분자의 적분식을 closed-form으로 계산할 수 없어서 conical frustum을 multi-variate Gaussian으로 근사했다는데,
conical frustum의 모양과 크기 범위에 대한 parameter가 주어진다면 frustum 내부의 점 \(x\) 에 sin 및 cos을 씌운 \(\gamma (x)\) 의 경우 \(x\) 에 대해 공간 적분할 수 있지 않나요?
A3 : frustum 내에 있는 모든 좌표에 \(\gamma\) 를 씌워서 공간 적분하는 것 자체가 말도 안 되게 복잡한 식이라 closed-form solution이 없기 때문에 frustum의 mean과 variance를 구해서 Gaussian으로 근사해서 expected value 구합니다
Q4 : 논문을 보면 frustum을 multi-variate Gaussian으로 근사하기 위해서는 먼저 \(F(x, o, d, \hat r, t_0, t_1)\) 의 mean, covariance를 계산해야 한다고 쓰여있던데
appendix를 보면 indicator function인 F의 mean과 covariance가 아니라 conical frustum의 \(r, t, \theta\) 범위를 이용해서 공간 적분해서 \(t, x, y\) 축의 mean과 variance를 계산하지 않나요?
A4 : 맞습니다. 논문에서 \(F(x, o, d, \hat r, t_0, t_1)\) 의 mean, covariance를 계산해야 한다고 언급되어 있는 것은 단순히 frustum 내부 범위에 속해있는 지점에 대해 적분을 통해 mean, variance를 구해야 한다는 뜻인 것 같습니다.
Q5 : NeRF에서 rendering할 때는 EWA volume splatting과 같은 좌표계 변환을 고려하지 않아도 되나요?
A5 : NeRF에서는 ray를 따라 MLP의 output을 alpha-compositing하여 직접 pixel 값을 얻어내므로 ray를 쓰기 위해 cam-to-world coordinate 변환만 필요하고, projection에 의한 non-linear 좌표계 변환과는 관련이 없다.
반면, Gaussian Splatting에서는 rendering할 때 3D Gaussian 자체를 직접 projection해서 쓰기 때문에 3D Gaussian covariance matrix on world-coordinate을 2D Gaussian covariance matrix on image-coordinate (ray-space)으로 projection해야 하므로 non-linear 좌표계 변환이 필요하다. 이를 위해 EWA volume splatting에 따라 non-linear transformation을 Taylor approx.하여 local affine transformation으로서 Jacobian을 사용한다
Q6 : camera origin과 pixel 중심을 잇는 ray가 image plane에 수직이 아닌 pixel의 경우 \(\hat r\) 과 \(d\) 를 어떻게 정의하지?
A6 : \(d\) 는 camera origin부터 pixel 중심까지의 거리 vector이고,
cone 단면의 \(\hat r\)은 \(d\) 와 수직인 방향으로 \(\frac{2}{\sqrt{12}}\) of pixel-width 이므로
cone 단면이 image plane 위에 있지 않은 꼴이 됨

Appendix

TBD

Code Review

IPE (integrated positional encoding)

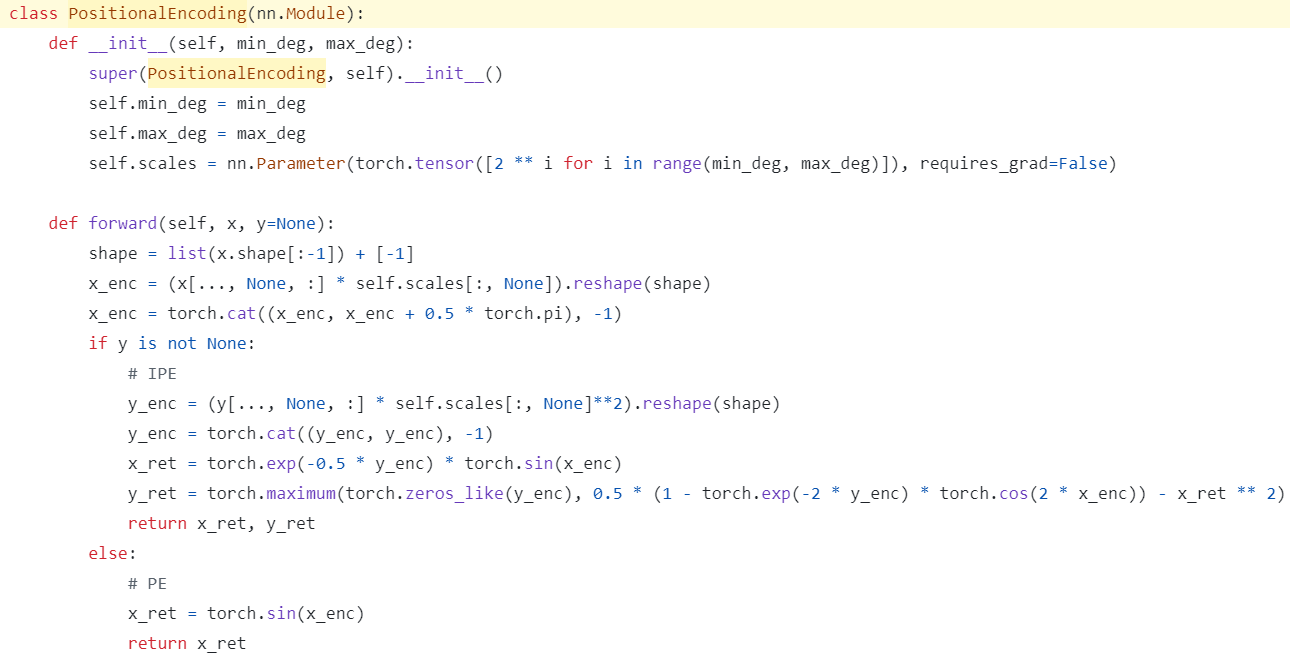
self.scales : \([2^l, \ldots, 2^{L-1}]\) of shape (\(L-l\),)
Let B : the number of cones
Let S : the number of samples (regions) (Gaussians)
case 1: Point-IPE
position은 Gaussian으로 근사해서 IPE 씀
- x : \(\mu\) of shape (B, S, 3) and y : \(diag(\Sigma)\) of shape (B, S, 3)
- x_enc : \(\mu_{r}\) , 즉 PE-basis-lifted mean of shape (B, S, (\(L-l\)) * 6)
  where 6 = 3 (3d-vector) * 2 (sin and cos)
  \(\mu_{r} = P \mu = \begin{pmatrix} \begin{matrix} 1 & 0 & 0 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 \\ 0 & 0 & 1 & 0 & 0 & 2\end{matrix} & \cdots & \begin{matrix} 2^{L-1} & 0 & 0 \\ 0 & 2^{L-1} & 0 \\ 0 & 0 & 2^{L-1}\end{matrix} \end{pmatrix}^T \begin{bmatrix} \mu_{x} \\ \mu_{y} \\ \mu_{z} \end{bmatrix}\)
  \(( \begin{bmatrix} \mu_{x} & \mu_{y} & \mu_{z} \\ \vdots & \vdots & \vdots \\ \mu_{x} & \mu_{y} & \mu_{z} \end{bmatrix} \circledast \begin{bmatrix} 2^l & 2^l & 2^l \\ \vdots & \vdots & \vdots \\ 2^{L-1} & 2^{L-1} & 2^{L-1} \end{bmatrix})\) .reshape(B, S, -1) \(= [\mu_{x}2^l, \mu_{y}2^l, \mu_{z}2^l, \ldots, \mu_{x}2^{L-1}, \mu_{y}2^{L-1}, \mu_{z}2^{L-1}]\) of shape ((\(L-l\)) * 3,)
  where \(\circledast\) is element-wise multiplication
  \(\cos{Px} = \sin{(Px + \frac{\pi}{2})}\)
- y_enc : \(diag(\Sigma_{r})\) , 즉 diagonal of PE-basis-lifted covariance of shape (B, S, (\(L-l\)) * 6)
  where 6 = 3 (3d-vector) * 2 (sin and cos)
  \(diag(\Sigma_{r}) = diag(P \Sigma P^T) = \left[ diag(\Sigma), 4 diag(\Sigma), \ldots , 4^{L-1}diag(\Sigma) \right]^T\)
  \(( \begin{bmatrix} \Sigma_{00} & \Sigma_{11} & \Sigma_{22} \\ \vdots & \vdots & \vdots \\ \Sigma_{00} & \Sigma_{11} & \Sigma_{22} \end{bmatrix} \circledast \begin{bmatrix} 4^l & 4^l & 4^l \\ \vdots & \vdots & \vdots \\ 4^{L-1} & 4^{L-1} & 4^{L-1} \end{bmatrix})\) .reshape(B, S, -1) \(= [\Sigma_{00}4^l, \Sigma_{11}4^l, \Sigma_{22}4^l, \ldots, \Sigma_{00}4^{L-1}, \Sigma_{11}4^{L-1}, \Sigma_{22}4^{L-1}]\)
- x_ret : \(\gamma (\mu, \Sigma)\) of shape (B, S, (\(L-l\)) * 6)
  \(\gamma (\mu, \Sigma) = E_{Px \sim N(\mu_{r}, \Sigma_{r})} [\begin{bmatrix} sin(Px) \\ cos(Px) \end{bmatrix}] = \begin{bmatrix} sin(\mu_{r}) \circledast exp(-\frac{1}{2}diag(\Sigma_{r})) \\ cos(\mu_{r}) \circledast exp(-\frac{1}{2}diag(\Sigma_{r})) \end{bmatrix}\)
- y_ret (covariance of \(\sin{z}\) where \(z \sim N(x_{enc}, y_{enc})\) ) 은 안 씀
case 2: View-Direction-PE
view-direction은 IPE 말고 그냥 PE 씀
- x : view-direction of shape (B, S, 3) and y : None
- x_enc : \(Pd\) , 즉 PE-basis-lifted view-direction of shape (B, S, (\(L-l\)) * 6)
- x_ret : \(\gamma (d)\) of shape (B, S, (\(L-l\)) * 6)
  \(\gamma (d) = \begin{bmatrix} sin(Pd) \\ cos(Pd) \end{bmatrix}\)