Mip-NeRF 360

Unbounded Anti-Aliased Neural Radiance Fields

Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields

Jonathan T. Barron, Ben Mildenhall, Dor Verbin, Pratul P. Srinivasan, Peter Hedman

paper :
https://arxiv.org/abs/2111.12077
project website :
https://jonbarron.info/mipnerf360/
pytorch code :
https://github.com/google-research/multinerf

핵심 요약 :

1. sampling 기법 개선하고, bounded scene으로 warp
2. non-linear scene, ray parameterization :
   disparity에 비례하도록 sampling 개선하고
   bounded space로 mapping하여
   임의의 방향과 깊이에 대한 unbounded scene 다룸
3. efficient proposal-based online-distillation :
   higher capacity MLP을 조금만 evaluate해서
   효율적으로 large scene 다룸
4. interval-distortion-based regularizer :
   artifacts 줄이기 위해
   step-function을 delta-function에 가깝게 regularize

Introduction

• 임의의 direction(360 degrees)과 임의의 depth로 unbounded 되어있는 scene 문제 해결
  • non-linear scene parameterization :
    sampling 개선하고 bounded space로 mapping하여
    임의의 방향과 깊이에 대한 unbounded scene 다룰 수 있음
  • online-distillation :
    higher capacity MLP을 조금만 evaluate해서 효율적으로 large scene 다룰 수 있음
  • distortion-based regularizer :
    artifacts 줄이기 위한 regularization
• NeRF model을 large unbounded scene에 적용하는 데 3가지 문제가 있다
  (자세한 내용은 스킵했는데 나중에 읽어보자)
  • Parametrization : Mip-NeRF는 3D coordinate가 bounded domain 안에 있는 경우만 처리 가능
  • Efficiency : large-and-detailed scene은 large MLP를 필요로 해서 expensive
  • Ambiguity : scene content가 임의의 distance에 있고 이는 only 적은 수의 ray로 관찰되기 때문에 inherent ambiguity 발생

Scene and Ray Parameterization

Ray Interval Parameterization

• Ray Interval Parameterization :
  samples의 경우 distance가 아니라 그의 역수인 disparity에 비례하여 분포하도록 하면
  가까이 있는 content는 많이 sampling하고 멀리 있는 content는 덜 sampling함으로써
  임의의 scale의 unbounded scene을 잘 다룰 수 있음

• NeRF :
  • NeRF에서는 distance에 비례하여 stratified uniform sampling 했음
  • 만약 NDC parameterization을 쓴다면
    NDC-space에서 distance에 비례하여 stratified uniform sampling 하면
    disparity (distance의 역수)에 비례하여 uniform sampling 한 것과 같은 효과를 가짐
    그 이유는 Normalized-Device-Coordinates 의 Linear in Disparity 파트 참고
  • 그런데 NDC는 single direction으로만 unbounded된 scene (front-facing camera)에 대해서만 적합하고
    모든 방향으로 unbounded된 scene에 대해서는 적합하지 않음
• Mip-NeRF 360 :
  • 처음부터 ray interval을 disparity (distance의 역수)에 비례하도록 [2] parameterize 한다

Ray Interval Parameterization in Disparity

• distance along ray를 t-space 또는 s-space에서 나타내자
  • t-space :
    Euclidean ray distance \(t \in [t_n, t_f]\)
    \(t = g^{-1}(s \cdot g(t_f) + (1-s) \cdot g(t_n))\)
  • s-space :
    normalized ray distance \(s \in [0, 1]\)
    \(s = \frac{g(t)-g(t_n)}{g(t_f)-g(t_n)}\)
• 사용 예시 :
  • \(g(x) = \frac{1}{x}\) 로 설정할 경우
    s-space에서 uniform sampling하면
    t-space에서 disparity에 비례하여 distributed
  • \(g(x) = log(x)\) 로 설정할 경우
    s-space에서 uniform sampling하면
    t-space에서는 logarithmic spacing [3] 으로 distributed
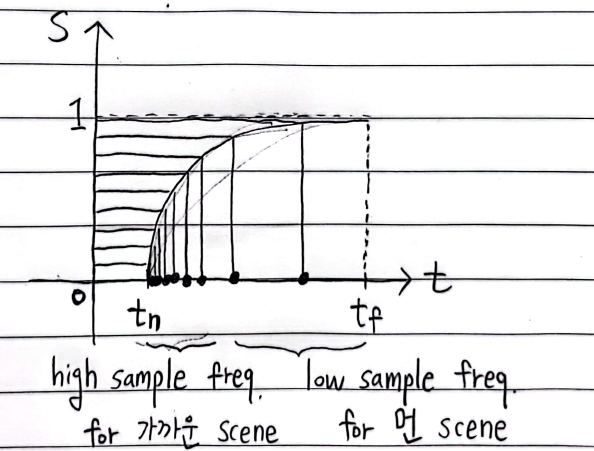
• 기존 NeRF 모델에서는 t-distance를 따라 uniform sampling했지만
  본 논문에서는 s-distance를 따라 uniform sampling하여 나타낸다

Scene Parameterization

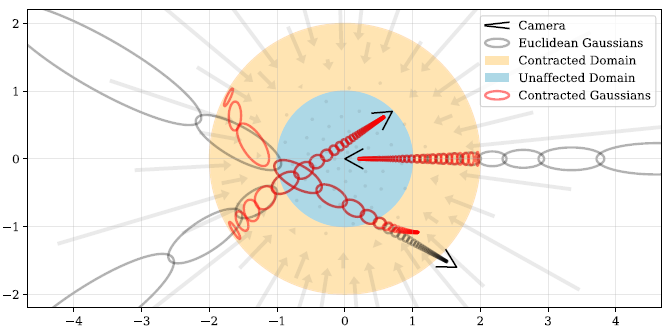
• Scene Parameterization :
  unbounded scene을 radius-2 내부의 bounded space로 mapping하기 위해 contract 함수를 사용
  ray parameterization을 할 때 disparity에 비례하게 sampling 했으므로
  contract 함수도 consistently disparity에 비례하게 bounded space로 mapping
  \(\rightarrow\) scene origin에서 cast된 ray의 경우 contract 함수를 적용한 후에는 아래 그림의 주황색 영역에서 일정한 길이의 interval을 가진다

• Define smooth coordinate-transformation function as \(f(x) : R^3 \rightarrow R^3\)
  • \(\mu, \Sigma\) 를 갖는 Gaussian에 non-linear \(f\) 를 적용하여 \(\mu_{c}, \Sigma_{c}\) 를 갖는 Gaussian으로 변형하려면
    \((\mu_{c}, \Sigma_{c}) = f(\mu, \Sigma) = (f(\mu), J_{f}(\mu) \Sigma J_{f}(\mu)^T)\)
    where \(f(x) \approx f(\mu) + J_{f}(\mu)(x-\mu)\) (linear approx.)
  • 이는 state transition model \(f = \text{contract}(x) = \begin{cases} x & \text{if} \| x \| \leq 1 \\ (2 - \frac{1}{\| x \|})(\frac{x}{\| x \|}) & \text{if} \| x \| \gt 1 \end{cases}\) 을 사용했을 때
    classic Extended Kalman filter [1] 와 수학적으로 동일
  • MipNeRF360에서는 contract 함수를
    point가 아니라 Euclidean 3D-space에 있는 Gaussian에 적용!
    또한
    모든 방향 (360 degress)에 대해 적용!
• IPE (integrated positional encoding) :
  • Mip-NeRF :
    \(\gamma (\mu, \Sigma) = \left[ \begin{bmatrix} sin(2^l \mu) \circledast exp(-\frac{1}{2} 4^l diag(\Sigma)) \\ cos(2^l \mu) \circledast exp(-\frac{1}{2} 4^l diag(\Sigma)) \end{bmatrix} \right]_{l=0}^{l=L-1}\)
  • Mip-NeRF 360 :
    \(\gamma (\text{contract}(\mu, \Sigma))\)
    where
    \(f(x) = \text{contract}(x) = \begin{cases} x & \text{if} \| x \| \leq 1 \\ (2 - \frac{1}{\| x \|})(\frac{x}{\| x \|}) & \text{if} \| x \| \gt 1 \end{cases}\)
    and \(f(x) \approx f(\mu) + J_{f}(\mu)(x-\mu)\)
    and \(f(\mu, \Sigma) = (f(\mu), J_{f}(\mu) \Sigma J_{f}(\mu)^T)\)
  • Mip-NeRF 360 procedure :
    casting cone
    \(\rightarrow\) uniform sampling in s-space
    \(\rightarrow\) contract 3D Gaussians in t-space into bounded sphere
    \(\rightarrow\) IPE \(\gamma\)
    \(\rightarrow\) MLP

contract 함수는 파란색 구(radius 1) 외부의 Gaussian(회색)을 주황색 영역(radius 1 ~ 2)의 Gaussian(빨간색)으로 mapping

Coarse-to-Fine Online Distillation

• 기존 NeRF :
  coarse-MLP와 fine-MLP

위의 그림은 Mip-NeRF, 아래의 그림은 Mip-NeRF 360

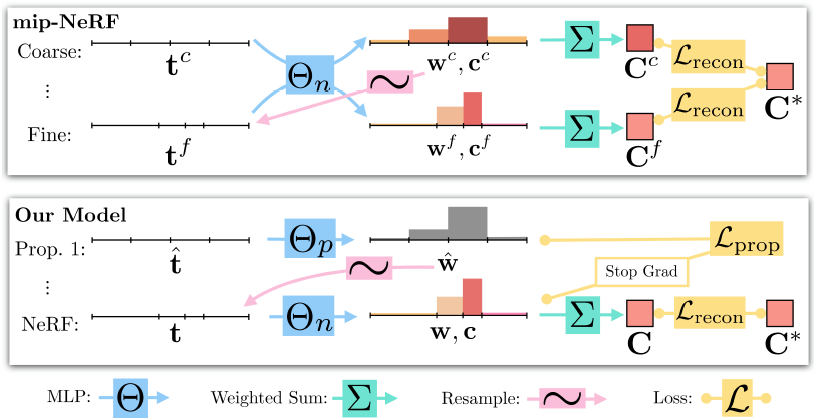
• Mip-NeRF 360 :
  proposal-MLP와 NeRF-MLP
  • small proposal-MLP는 many samples로 여러 번 evaluate하고,
    large NeRF-MLP는 less samples로 딱 한 번 evaluate함으로써
    Mip-NeRF보다 조금만 더 costly하지만 훨씬 더 higher capacity를 가진 것과 같은 효과
    \(\rightarrow\) 효율적으로 large unbounded scene을 표현하기에 적절
    distill 효과가 좋아서 proposal-MLP의 경우 크기 줄이더라도 accuracy 감소하지 않음
  • small proposal-MLP :
    • color 말고 volume density만 예측하여 weight \(\hat w\) 구함
  • large NeRF-MLP :
    • color, volume density 예측하여 weight \(w\) 구하고 rendering
• Loss :
  아래 두 가지 loss로 각 MLP를 jointly train
  • reconstruction loss :
    • large NeRF-MLP에서 rendering해서 구함
      기존 NeRF 방식과 동일
    • GT-image를 supervision으로 하여 NeRF-MLP만 업데이트
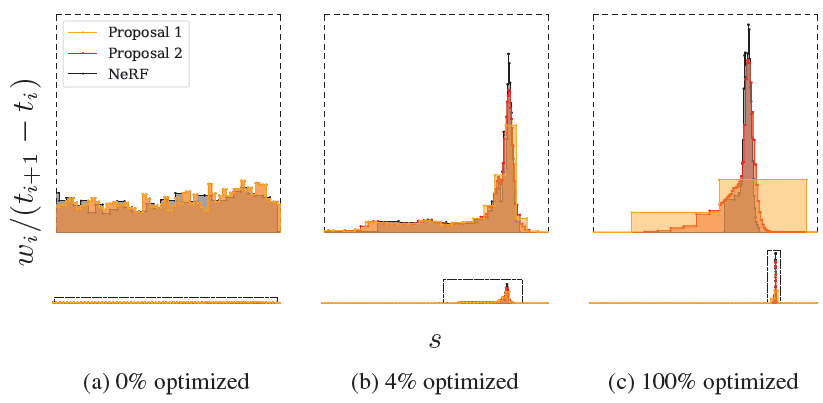
  • proposal loss :
    • 두 MLP의 weight histogram이 consistent하도록 함
      즉, proposal-MLP의 weight histogram이 NeRF-MLP의 weight histogram을 따라잡도록 함
      (Mip-NeRF 계열은 point가 아니라 interval 별로 weight를 구하므로 histogram을 만들 수 있음)
    • NeRF-MLP의 weight를 supervision으로 하여 proposal-MLP만 업데이트
      (online distillation of NeRF-MLP’s knowledge into proposal-MLP)
    • 문제 :
      하나의 histogram bin의 distribution에 대해 아무 것도 가정할 수 없음
      (하나의 bin의 distribution이 uniform일 수도 있고 특정 지점에 몰빵된 delta function일 수도 있음…)
      coarse \(\hat t\) 와 fine \(t\) (bins)가 매우 다를 수 있음
    • 가정 :
      두 개의 histogram이 매우 달라보이더라도
      둘 다 어떤 하나의 동일한 (underlying continuous) true mass distribution으로부터 유래되었다고 설명할 수 있다면 둘의 차이인 loss는 0 이다
    • 위의 가정에 따라
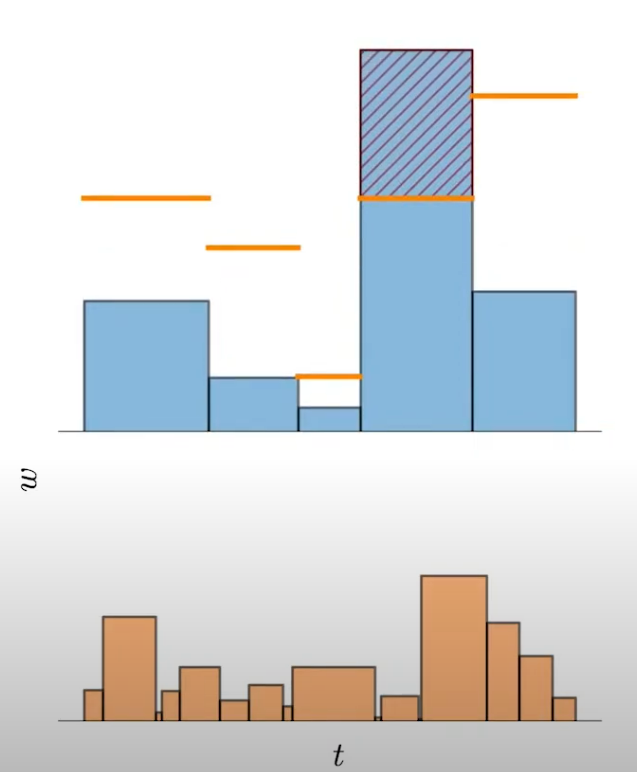
      NeRF-MLP (\(t\), \(w\))의 구간 \(T\) 와 겹치는 모든 proposal-MLP의 weight \(\hat w_{j}\) 를 더해서 아래와 같이 NeRF-MLP weight \(w\) 의 upper bound를 구하자
      \(\text{bound}(\hat t, \hat w, T) = \sum_{j: T \cap \hat T_{j} \neq \emptyset} \hat w_{j}\)
      (\(t\) 와 \(\hat t\) 가 정렬되어 있으므로 summed-area table로 효율적으로 계산 가능)
    • 만약 두 개의 histogram이 consistent하다면,
      NeRF-MLP (\(t\), \(w\))의 모든 구간 (\(T_i, w_i\))에 대해
      \(w_i \leq \text{bound}(\hat t, \hat w, T_i)\) 이어야 한다
      \(\rightarrow\)
      아래와 같이 proposal loss는 이를 위반하는 경우에 해당한다
      \(L_{prop}(t, w, \hat t, \hat w) = \sum_{i}\frac{1}{w_i} \text{max}(0, w_i - \text{bound}(\hat t, \hat w, T_i))^2\)
    • 즉, proposal-MLP가 NeRF-MLP의 upper-bound를 형성하도록 한다는 것은
      proposal-MLP가 NeRF-MLP histogram의 개형을 따라잡도록 하는 효과!
    • proposal loss가 asymmetirc loss인 이유 :
      proposal-MLP가 NeRF-MLP보다 coarse하기 때문에
      proposal-MLP weight가 NeRF-MLP weight의 upper bound를 형성하는 게 (overestimate) 당연하고,
      proposal-MLP weight가 NeRF-MLP weight를 underestimate (\(\text{bound}(\hat t, \hat w, T_i) < w_i\)) 하는 경우에만 penalize
    • proposal loss term에서 \(w_i\) 로 나누는 이유 :
      bound가 0일 때 \(\frac{dL_{prop}}{d\text{bound}} = \sum_{i} \frac{1}{w_i} \cdot 2 \cdot \text{max}(0, w_i - \text{bound}) \cdot (-1) = -2\sum_{i}1\) 와 같이
      \(w_i\) 크기와 상관없이 gradient 값이 상수값이 되어 균등하게 penalize하여 optimization에 도움됨

위의 histogram이 NeRF-MLP, 아래의 histogram이 proposal-MLP, 보통 proposal-MLP가 coarse하고 NeRF-MLP가 fine한데 여기선 반대로 그려져 있음

fine NeRF-MLP는 점점 scene content의 surface 쪽으로 weight가 집중되고, coarse proposal-MLP는 이를 따라잡으며 upper bound를 형성

Regularization for Interval-Based Models

• Artifacts :
  NeRF 계열은 pose 문제 때문에 두 가지 주된 artifacts가 나타난다
  • floater :
    특정 view를 너무 잘 설명하려던 나머지
    실제로 물체가 존재하지 않는 small disconnected regions of dense volume에서 불필요하게 opacity를 예측하여
    다른 view에서 보면 반투명한 blurry cloud처럼 보이는 부분
  • background collapse :
    멀리 있는 surface가
    반투명한 가까운 content로 잘못 모델링된 경우

반투명하게 떠다니는 게 floater, 좌하단에서 background surface가 가깝게 보이는 게 background collapse

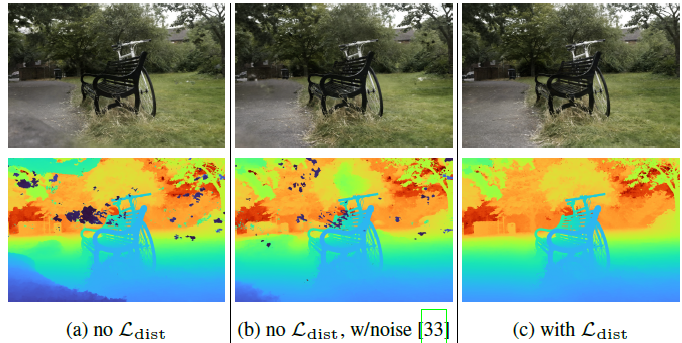
• Artifacts 완화 :
  • 기존 NeRF : random noise
    NeRF-Code 의 raw2outputs()에서 볼 수 있듯이
    raw-opacity에 random noise 더해서 \(\sigma_{i}\) 구함
    noise 덕분에 불필요한 특정 지점에 overfit 되는 게 아니라 일관성 있게 학습
    But, 부분적으로 artifacts 완화하고 reconstruction quality를 떨어뜨림
  • Mip-NeRF 360 : regularize
    ray-sampling은 이미 했고 weight를 구할 때
    물체가 있을만한 정확한 지점에서 집중적으로 예측하여
    부정확한 지점에서의 불필요한 예측을 억제
• Regularization for Interval-Based Models :
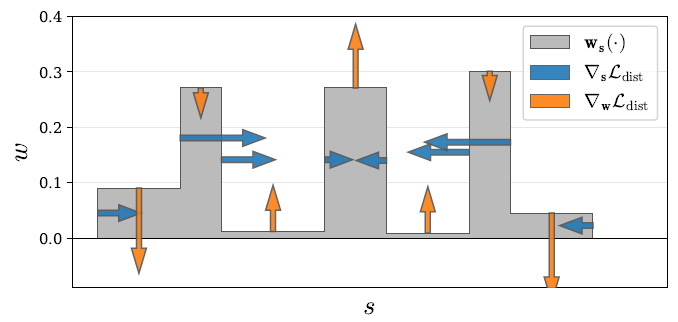
  • distortion loss :
    step-function인 weight-histogram \(s, w\) 을 regularize하기 위해
    \(L_{dist}(s, w) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} w_s(u)w_s(v)|u-v|d_ud_v\)
    • NeRF-MLP 업데이트할 때 artifacts 완화(regularization)하는 역할
  • 위의 loss를 최소화하기 위해선
    \(w\) 를 매우 작은 \(|u-v|\) 에 몰빵하면 된다
    즉, 위의 loss term만 있을 경우 histogram(step-function)이 delta-function에 가까워지면 된다
  • t-distance 대신 s-distance 사용 :
    t-distance 사용하면 먼 거리에 있는 interval 길이가 길기 때문에 무조건 먼 거리의 interval 쪽으로 distortion 됨
    s-distance 기준으로 weight-histogram 만들어서 distortion loss 구하자!

• distortion loss :
  • weight \(w\) 는 step-function (각 interval 안에선 constant) 이므로
    아래와 같이 계산하기 쉬운 꼴로 유도할 수 있음
    \(L_{dist}(s, w) = \sum_{i, j} w_i w_j |\frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2}| + \frac{1}{3} \sum_{i} w_i^2 (s_{i+1} - s_i)\)
  • 유도 과정 :
    출처 : https://charlieppark.kr/
    • \(L_{dist}(s, w) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} w_s(u)w_s(v)|u-v|d_ud_v\)
      where \(w_s(u) = w_i\) for \(u \in [s_i, s_{i+1})\)
    • case 1. \(u, v\) are in the same interval : \(u, v \in [s_i, s_{i+1})\)
      \(\int_{s_i}^{s_{i+1}}\int_{s_i}^{s_{i+1}}w_i^2|u-v|d_ud_v\)
      \(= w_i^2 \frac{(s_{i+1}-s_i)^3}{3}\)
    • case 2. \(u, v\) are in different intervals : \(u \in [s_i, s_{i+1}), v \in [s_j, s_{j+1})\) where \(i \neq j\)
      \(\int_{s_i}^{s_{i+1}}\int_{s_j}^{s_{j+1}}w_iw_j|u-v|d_ud_v\)
      \(\simeq \int_{s_i}^{s_{i+1}}\int_{s_j}^{s_{j+1}}w_iw_j|\frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2}|d_ud_v\)
      \(= w_iw_j|\frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2}|\cdot (s_{i+1}-s_i)(s_{j+1}-s_j)\)
    • \[L_{dist}(s, w) = \sum_{i} w_i^2 \frac{(s_{i+1}-s_i)^3}{3} + \sum_{i, j} w_iw_j|\frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2}|\cdot (s_{i+1}-s_i)(s_{j+1}-s_j)\]
    • \((s_{i+1} - s_i)^2\) 항과 \((s_{i+1}-s_i)(s_{j+1}-s_j)\) 항을 제거하여 학습의 안정성을 높임
      \(L_{dist}(s, w) = \frac{1}{3} \sum_{i} w_i^2 (s_{i+1} - s_i) + \sum_{i, j} w_i w_j |\frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2}|\)
    • \(u, v\) 가 same interval에 있을 경우에는 \((s_{i+1}-s_i)\) 항으로 각 구간의 (weighted) 너비를 줄이고,
      \(u, v\) 가 different interval에 있을 경우에는 \(|\frac{s_i + s_{i+1}}{2} - \frac{s_j + s_{j+1}}{2}|\) 항으로 두 구간 사이의 (weighted) 중심 거리를 줄임
      이 원리를 통해
      entire ray is unoccupied이 가능하다면 모든 weight가 0에 가까워지려 하고
      불가능하다면 weight를 few interval에 몰빵하려 해서
      weight-histogram이 delta-function에 가까워질 수 있음

Optimization

• Setting :
  • proposal-MLPs with 4 layers and 256 hidden_dim
    two proposal-MLP \((\hat s^0, \hat w^0)\) and \((\hat s^1, \hat w^1)\) each using 64 samples
  • NeRF-MLP \((s, w)\) with 8 layers and 1024 hidden_dim
    one NeRF-MLP using 32 samples
    (NeRF와 Mip-NeRF에서는 MLP with 8 layers and 256 hidden_dim 사용했었음)
  • total loss :
    \(L_{tot} = L_{recon}(C(t), C^{\ast}) + \lambda L_{dist}(s, w) + \sum_{k=0}^{1}L_{prop}(s, w, \hat s^k, \hat w^k)\)
    averaged over all rays in batch
    where author sets \(\lambda = 0.01\)
  • \(L_{recon}\) and \(L_{dist}\) for NeRF-MLP
    • \(L_{recon}(x, x^{\ast}) = \sqrt{(x - x^{\ast})^2 + \epsilon^{2}}\) : Charbonnier loss
      slightly more stable than MSE
  • \(L_{prop}\) for proposal-MLP
  • learning schedule :
    250k iter. with batch size \(2^{14}\)
    Adam optimizer with \(\beta_{1} = 0.9, \beta_{2} = 0.999, \epsilon = 10^{-6}\)
    lr is annealed log-linearly from \(2 \times 10^{-3}\) to \(2 \times 10^{-5}\)
    warm-up phase of 512 iter.
    gradient clipping to norm of \(10^{-3}\)

Conclusion

• Mip-NeRF extension for real-world unbounded scenes with unconstrained camera depth and orientations
• (Kalman-like) scene and ray parameterization
• efficient proposal-based coarse-to-fine distillation framework
• interval-distortion-based regularizer
• Mip-NeRF에 비해 57% reduction in MSE

Question

• Q&A reference : 3DGS online study
• Q1 : 아래의 문구가 이해되지 않습니다
  recall that the “bins” of those histograms \(t\) and \(\hat t\) need not be similar; indeed, if the proposal MLP successfully culls the set of distances where scene content exists, \(\hat t\) and \(t\) will be highly dissimilar
• A1 : 아래 사진의 (c)에서처럼 충분히 optimize되어 만약 coarse proposal-MLP가 이미 scene content가 있는 곳을 성공적으로 예측하고 있다면 이를 이용한 fine NeRF-MLP의 fine-samples는 그 곳에 더 촘촘히 존재할 것이므로 bin 간격이 달라져서 두 histogram이 크게 달라보인다
  달라보이더라도 두 개의 histogram이 어떤 하나의 (true continuous underlying) mass distribution에서 유래되었다고 설명할 수 있으면 둘의 차이가 0이라고 가정하여 upper bound를 이용해서 proposal loss 만듬

• Q2 : 갑자기 든 생각인데 Mip-NeRF 360의 sampling 기법과 contract 함수가 background collapse의 원인이 될 수도 있지 않을까요?
  disparity에 비례하게 sampling하므로 먼 거리에 대해서는 덜 sampling한 채로 bounded space로 warp하는데,
  먼 거리의 content에 대해 정보가 부족한 채로 warp하는 과정에서 왜곡이 일어날 수 있을 것 같다
• A2 : 그럴 수 있을 것 같습니다

Code Review

TBD

Appendix

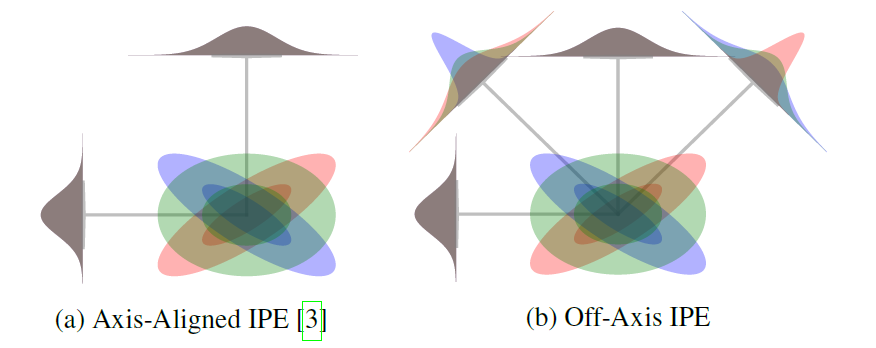
Off-Axis Positional Encoding

• Mip-NeRF의 IPE 식 :
  PE-basis를 identity matrix로 설정하였으므로
  \(P = \begin{pmatrix} \begin{matrix} 1 & 0 & 0 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 \\ 0 & 0 & 1 & 0 & 0 & 2\end{matrix} & \cdots & \begin{matrix} 2^{L-1} & 0 & 0 \\ 0 & 2^{L-1} & 0 \\ 0 & 0 & 2^{L-1}\end{matrix} \end{pmatrix}^T\)
  \(diag(\Sigma_{r})\) 계산을 위해 \(diag(\Sigma)\) 만 알면 됨

• Mip-NeRF 360의 IPE 식 :
  IPE를 하기 전에 우선 Gaussian을 radius-2의 구 안으로 contract 해야 해서
  어차피 full covariance matrix \(\Sigma\) 가 필요하므로
  PE-basis를 아래와 같이 둔다
  (\(P\) 의 각 column이 twice-tessellated icosahedron(두 번 테셀레이션 된 정이십면체)의 unit-norm vertex이고, 음의 같은 방향으로 중복된 vertex는 제거)
  \(P = \begin{bmatrix} 0.8506508 & 0 & 0.5257311 \\ 0.809017 & 0.5 & 0.309017 \\ 0.5257311 & 0.8506508 & 0 \\ 1 & 0 & 0 \\ 0.809017 & 0.5 & -0.309017 \\ 0.8506508 & 0 & -0.5257311 \\ 0.309017 & 0.809017 & -0.5 \\ 0 & 0.5257311 & -0.8506508 \\ 0.5 & 0.309017 & -0.809017 \\ 0 & 1 & 0 \\ -0.5257311 & 0.8506508 & 0 \\ -0.309017 & 0.809017 & -0.5 \\ 0 & 0.5257311 & 0.8506508 \\ -0.309017 & 0.809017 & 0.5 \\ 0.309017 & 0.809017 & 0.5 \\ 0.5 & 0.309017 & 0.809017 \\ 0.5 & -0.309017 & 0.809017 \\ 0 & 1 & 0 \\ -0.5 & 0.309017 & 0.809017 \\ -0.809017 & 0.5 & 0.309017 \\ -0.809017 & 0.5 & -0.309017 \end{bmatrix}\)

column of PE-basis P

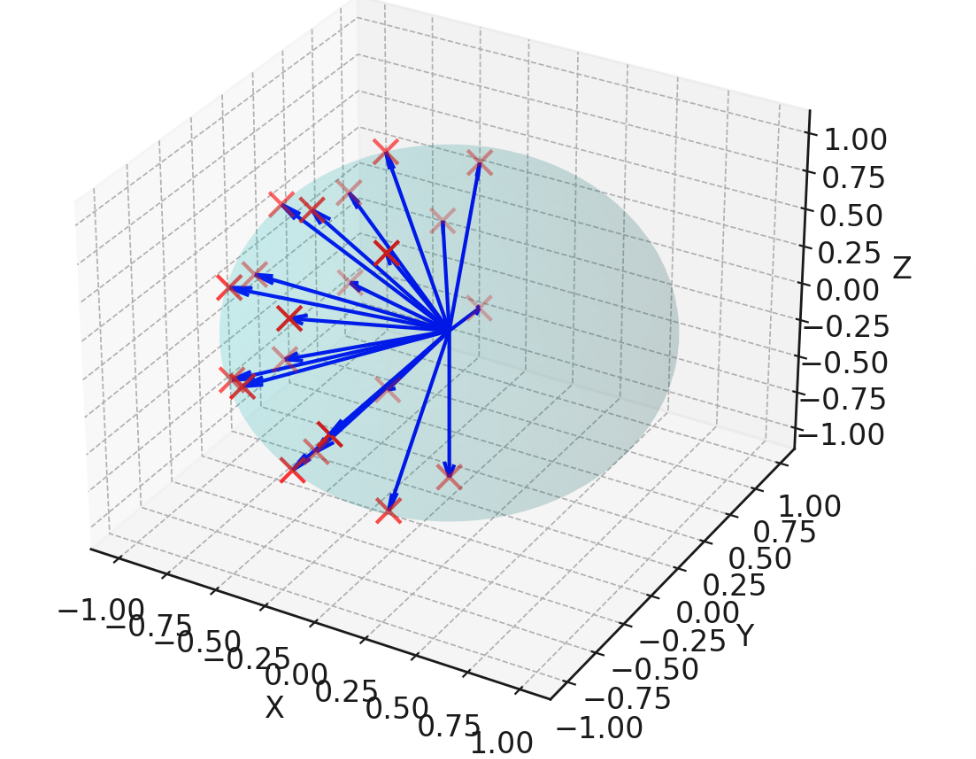
• Mip-NeRF 360의 IPE 식 :
  • off-axis feature를 쓰면 anisotropic Gaussian의 모양까지 잘 encode할 수 있어서 rendering quality 향상
  • IPE 식에서 \(diag(\Sigma_{r}) = diag(P \Sigma P^T)\) 를 계산할 때
    large \(P\) matrix에 대해 행렬곱을 하려면 너무 비싸므로
    \(diag(P \Sigma P^T)\) 대신 \(\text{sum}(P^T \circledast (\Sigma P^T), \text{dim}=0, \text{keepdim=False})\) 로 계산하면
    Mip-NeRF의 Axis-Aligned IPE보다 Mip-NeRF 360의 Off-Axis IPE가 살짝만 더 expensive

왼쪽은 Mip-NeRF의 Axis-Aligned IPE이고, 오른쪽은 Mip-NeRF 360의 Off-Axis IPE, 각 encoding basis로 Gaussian을 projection해서 marginal distribution을 구했을 때 Off-Axis Projection을 해야 Gaussian shape를 더 잘 구분할 수 있음

Annealing Weight

• proposal-weight PDF로 fine-sampling할 때
  proposal-weight \(\hat w\) 대신 \(\hat w_n \propto \hat w^{\frac{bn/N}{(b-1)n/N+1}}\)
  where \(n\) iter. out of \(N\) steps
  where 지수부분 \(\frac{bn/N}{(b-1)n/N+1}\) 은 0부터 1까지 빠르게 증가
  where bias hyper-param. \(b=10\)

• \(n=0\) 일 때는 \(\hat w_0 \propto 1\) 을 따라 sampling하고
  \(n=N\) 일 때는 \(\hat w_N \propto \hat w\) 을 따라 sampling하므로
  훈련 초기 단계에서 NeRF-MLP가 더 다양한 proposal-interval 범위를 모험(exploration)할 수 있도록 함

Dilation

• proposal-weight PDF로 fine-sampling할 때
  aliasing-artifacts 줄이기 위해 먼저 proposal-histogram \((\hat t, \hat w)\) 을 dilate

• 이유 :
  proposal-MLP는 오직 input ray로만 supervised되므로
  특정 각도에 대해서만 예측 가능할 수 있다
  (proposal-MLP는 rotationally aliased)

• 해결 : dilation
  proposal-MLP의 interval을 넓힘으로써 anti-aliasing
  왜 interval 넓히면 anti-aliasing??? weight 변화가 급격하지 않아서???

  • Step 1) proposal-MLP의 histogram \((\hat s, \hat w)\) 에서 weight를 구간 길이로 나눈 뒤 normalize해서 probability density \(\hat p\) 로 만듬
    \(\hat p_i = \frac{\hat w_i}{(\hat s_{i+1} - \hat s_{i})}\)
  • Step 2) dilation factor (얼만큼 각 구간을 넓힐지) 계산
    fine intervals 개수가 많을수록 평균적인 구간 길이가 짧아지고 dilation factor가 작아짐
    \(\epsilon = \frac{a}{\prod_{k'=1}^{k-1} n_{k'}} + b\)
    where \(k\) 번째 coarse-to-fine resampling 단계에서 \(n_k\) 개의 fine intervals을 resample
  • Step 3) 각 구간 \([\hat s_{i}, \hat s_{i+1}]\) 를 \([\hat s_{i} - \epsilon, \hat s_{i+1} + \epsilon]\) 로 확장
  • Step 4) 확장한 각 구간마다 probability density 최대값을 구함
    \(\text{max}_{\hat s - \epsilon \leq s \lt \hat s + \epsilon} \hat p_{\hat s} (s)\)
    where \(\hat p_{\hat s} (s)\) is interpolation into the step function defined by \(\hat s, \hat p\) at \(s\)
  • Step 5) 다시 구간 길이로 곱한 뒤 normalize해서 weight-histogram으로 만듬

Sampling

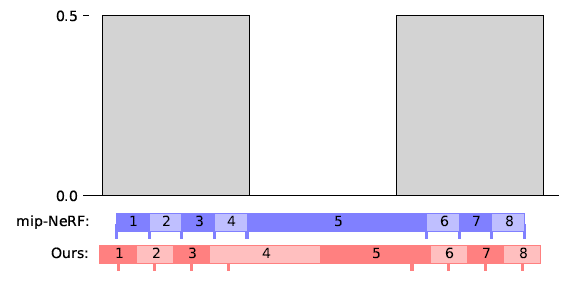
• Mip-NeRF :
  • sampling 방식 :
    coarse-histogram으로부터 \(n+1\) 개의 t-distance를 sampling한 뒤
    각 fine-samples를 끝점으로 하여 \(n\) 개의 fine-intervals을 얻음
  • 단점 :
    아래 그림과 같이 samples가 coarse-histogram 각 구간의 전범위를 전부 span하지 못하여
    일부 구간이 sampling에서 제외되므로(충분히 다뤄지지 않으므로)
    coarse-histogram의 영향을 서서히 약화시킴
• Mip-NeRF 360 :
  • sampling 방식 :
    coarse-histogram으로부터 \(n\) 개의 s-distance를 sampling한 뒤
    각 구간의 mid-points \(n-1\) 개와 coarse-sample의 양끝 점 2개를 끝점으로 하여 \(n\) 개의 fine-intervals를 얻음
  • 효과 :
    samples가 coarse-histogram의 처음과 끝 구간도 전부 span하고
    불규칙한 resampling도 감소하여
    rendering quality는 큰 변화 없지만 aliasing 줄이는 데 도움됨

sampling한 건 막대로 표시하였고, 이로부터 8개의 fine-intervals를 얻음

Background Colors

• NeRF와 Mip-NeRF :
  • 훈련시킬 때 background color를 black or white로 설정하는데
    scene recon.할 때 background가 반투명하게 reconstruct될 수도 있다
  • 문제 :
    반투명한 background는
    view synthesis 자체에는 문제가 없지만
    ray-termination-distance가 부정확하여
    부정확한 depth-map을 생성할 수 있다
• Mip-NeRF 360 :
  • Blender dataset :
    이전과 똑같이 black or white로 background color 설정
  • 360 and LLFF dataset :
    훈련시킬 때 background color를 \([0, 1]^3\) 사이의 random color로 설정하여
    scene recon.할 때 fully-opaque background이도록 함

Implementation Details

• \(\mu, \Sigma\) 를 갖는 Gaussian에 non-linear \(f\) 를 적용하여 \(\mu_{c}, \Sigma_{c}\) 를 갖는 Gaussian으로 변형하기 위해
  \((\mu_{c}, \Sigma_{c}) = (f(\mu), J_{f}(\mu) \Sigma J_{f}(\mu)^T)\)
  where \(f(x) \approx f(\mu) + J_{f}(\mu)(x-\mu)\) (linear approx.)
• 이 때, \(J_{f}(\mu)\) matrix는 autodiff framework로 직접 계산할 수 있지만
  사실 우리는 직접 explicitly matrix를 만들 필요가 없음
• less expensive 계산 위해
  \(J_{f}(\mu)\)와 행렬곱하는 것과 똑같은 역할을 하는 함수를 이용
  e.g. \(J_{f}(\mu) \Sigma J_{f}(\mu)^T\) 계산 위해
  Jax의 linearize operator [4]를 두 번 적용