Monocular Depth Estimation with Left Right Consistency

Unsupervised Monocular Depth Estimation with Left-Right Consistency

Clement Godard, Oisin Mac Aodha, Gabriel J. Brostow

paper :
https://arxiv.org/abs/1609.03677
referenced blog :
https://blog.naver.com/dncks1107/223104039030

핵심 요약 :

unsupervised mono (single image as input) depth estimation

unsupervised learning by reconstruction loss

need for binocular stereo image pairs at training

novel loss function : left-right consistency loss b.w. disparity maps

Backgrounds

Stereo Depth Estimation

인간은 물체를 두 개의 눈을 통해 바라보고 그 차이를 이용하여 대상까지의 거리를 예측한다. AI는 이러한 인간의 시각 시스템을 모방하여 stereo depth estimation을 통해 대상까지의 깊이를 추정할 수 있다.
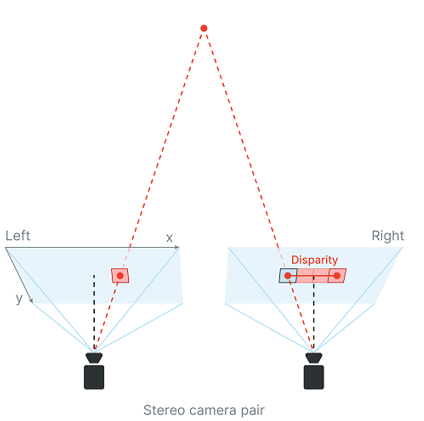
Stereo image란 카메라 두 대를 사용하여 찍은 두 이미지를 의미하고, disparity는 한 쌍의 stereo image 간의 pixel difference를 의미한다.
stereo depth estimation은 stereo image 한 쌍 (left image, right image)을 network의 input으로 넣어 이미지 간의 disparity를 통해 depth를 추정하는 것이다.
stereo depth estimation의 경우, epipolar geometry라는 수학적 원리에 의해 depth를 계산하기 때문에 비교적 정확하지만 카메라와 물체 사이의 거리가 멀어질수록 불리해진다.

Monocular Depth Estimation

monocular depth estimation은 위와 달리 하나의 image만을 network의 input으로 넣어 depth를 추정하는 방법이다. 물론 test-phase에서 하나의 image를 input으로 넣겠다는 의미이고, 이 논문의 경우 training loss를 구할 때는 stereo image 쌍을 모두 이용하였다.
mono depth estimation의 경우, 믿을 만한 근거(epipolar geometry와 같은 수학적 원리)가 없기 때문에 정확도가 떨어지지만 하나의 image만 input으로 넣기 때문에 전처리 과정이 간단하고 메모리도 덜 필요로 하여, 어느 정도의 정확도만 확보된다면 실생활에서 적용 가능 범위가 더 넓다.

Monocular and Stereo Camera

monocular camera : 특정 시간 t에 한 개의 camera 렌즈를 사용
stereo camera : 특정 시간 t에 6~7cm 떨어진 두 개의 camera 렌즈를 사용

Abstract

기존의 supervised depth estimation 방식은 성능은 좋지만, 구하기 어려운 pixel-wise ground-truth depth data를 대량으로 필요로 한다는 단점이 있었다. 그래서 본 논문의 저자는 ground-truth depth 정보가 없는 stereo image 쌍으로부터 pixel-level depth map을 합성하도록 훈련하는 unsupervised depth estimation 방식을 제안한다. 효과적인 표기를 위해 아래의 notation을 사용하자.
\(I^{l}\) : left image
\(I^{r}\) : right image
\(d^{r}\) : disparity map from left to right
\(d^{l}\) : disparity map from right to left

그렇다면 stereo image \(I^{l}, I^{r}\)로부터 어떻게 depth를 추정할까? image rectfiication을 거친 뒤, depth를 직접 예측하는 게 아니라 우선 두 개의 disparity map (dense correspondence field) \(d^{r}, d^{l}\) 을 생성한다. 여기서 disparity map이란, image의 한 pixel이 다른 image의 어느 pixel에 대응하는지에 대한 정보를 의미한다. 이후 \(I^{l}\)과 \(d^{r}\)을 이용하여 \(I^{r \ast} = I^{l}(d^{r})\)을 reconstruct하고, \(I^{r}\)과 \(d^{l}\)을 이용하여 \(I^{l \ast} = I^{r}(d^{l})\)을 reconstruct 한 뒤, \(I^{r \ast}\)과 \(I^{r}\) 간의 reconstruction loss와 \(I^{l \ast}\)과 \(I^{l}\) 간의 reconstruction loss를 이용하여 모델을 학습시킨다. 그런데 reconstruction loss만 사용한다면 depth image의 quality가 저하된다고 한다. 따라서 본 논문의 저자는 \(d^{r}\)과 (projected \(d^{l}\)) = \(d^{l}(d^{r})\) 간의 차이도 고려하는 left-right disparity consistency loss라는 논문의 핵심 아이디어를 제안하였다.

Contribution

end-to-end unsupervised monocular depth estimation
new training loss that enforces left-right disparity consistency

supervised stereo depth estimation

DispNet (Mayer et al.) :
directly predict the disparity for each pixel by regression loss
단점 : need lots of ground-truth disparity data and stereo image pairs, which are hard to obtain in real-world

unsupervised depth estimation

Deep Stereo (Flynne et al.) :
select pixels from nearby images and generate new views by using the relative pose of multiple cameras
단점 : At test phase, need several nearby posed images, which is not mono depth estimation

Deep3D (Xie et al.) :
make a distribution over all the possible disparities for each pixel and generate right view from an input left image by using image reconstruction loss
단점 : need much memory if there are lots of possible disparities. So, it is not scalable to bigger output resolutions

Garg et al. :
본 논문과 유사하게 unsupervised mono depth estimation with image reconstruction loss
단점 : not fully differentiable (이를 보완하고자 Taylor approximation을 수행하긴 했지만 이는 more challenging to optimize)

Method

Depth Estimation as Image Reconstruction

핵심 아이디어 : calibrated binocular(stereo) camera로 같은 시간에 찍은 한 쌍의 stereo image가 주어졌을 때, 하나의 image로부터 다른 image를 reconstruct 할 수 있다면 그 장면의 3D 구조를 알 수 있다!

우선 a stereo image pair에 대해 image rectification을 거친 뒤 만약 disparity map을 얻었다면 아래의 도식에 의해 depth map으로 변환할 수 있다.

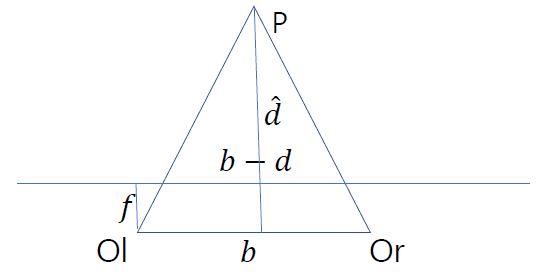
\(b\) : baseline distance between two camera centers (상수)
\(f\) : camera focal length (상수)
가로로 뻗은 직선 : rectified image plane
\(d\) : predicted disparity
\(\hat d\) : depth
\(b : \hat d = b - d : \hat d - f\) 이므로 \(\hat d (b - d) = b (\hat d - f)\) 이고,
이를 정리하면 \(\hat d \cdot d = bf\), 즉 \(\hat d = \frac{bf}{d}\) 이다
만약 disparity \(d = x_{r} - x_{l}\) 과 depth \(Z = \hat d\)를 얻었다면, 아래의 도식으로 3D point 좌표 \(X, Y\) 도 알 수 있다.
\(x = \frac{f_x \cdot X}{Z} + p_x\)

Depth Estimation Network

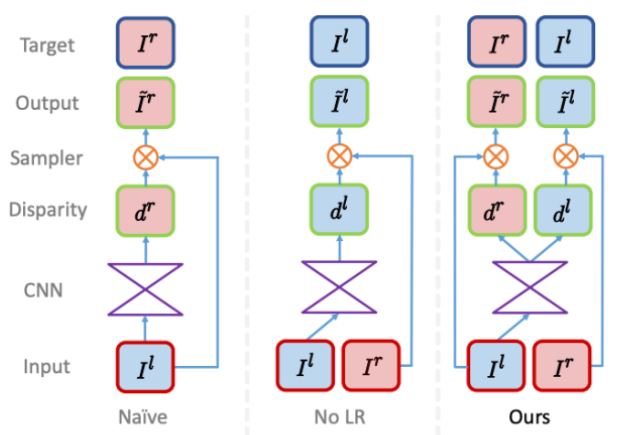
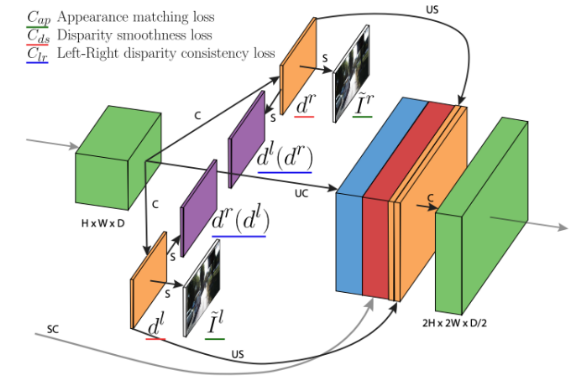
위의 figure에서 볼 수 있듯이 Naive 버전은 input left image와 align할 output reconstructed left image가 없다. 한편, No LR 버전은 align할 output reconstructed left image는 존재하지만, left-right consistency가 보장되지 않기 때문에 'texture-copy' artifacts와 depth discontinuities(boundaries)에서의 errors가 생기는 문제가 있다. 본 논문의 model은 disparity \(d^{r}, d^{l}\) 을 동시에 추론함으로써 이러한 문제들을 모두 해결하였다.
위의 figure에서 볼 수 있듯이 mono depth estimation이므로 CNN의 input으로 left image만을 넣어서 disparity dr, dl 을 동시에 추론하였다. 이를 통해 두 disparity 간의 consistency를 어느 정도 강제할 수 있고 결과적으로 더 정확한 depth estimation이 가능해진다. 참고로 right image는 image reconstruction과 training loss를 구할 때만 사용된다.
disparity를 구한 뒤에는 bilinear sampler와 backward mapping을 통해 image reconstruction을 수행한다. 이 때, STN(spatial transformer network)의 bilinear sampler를 이용하기 때문에 위의 일련의 과정은 fully convolutional and fully differentiable하다.

backward mapping :
결과 영상으로 mapping 되는 원본 영상에서의 좌표를 계산하여 해당 밝기값을 가져온다. 이 때, 원본 영상에서의 좌표는 실숫값이므로 bilinear interpolation (output pixel = the weighted sum of four input pixel)을 사용한다. 결과 영상의 각 pixel에 대해 값을 가져오므로 forward mapping에서의 hole 발생은 일어나지 않는다.

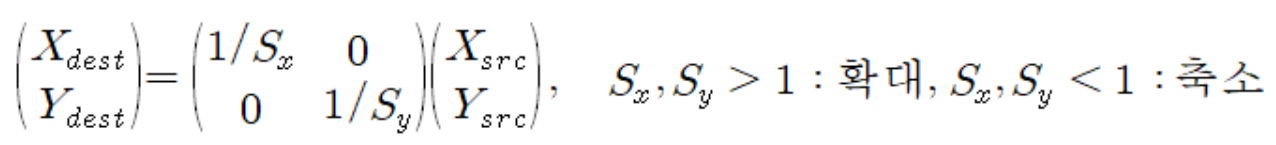
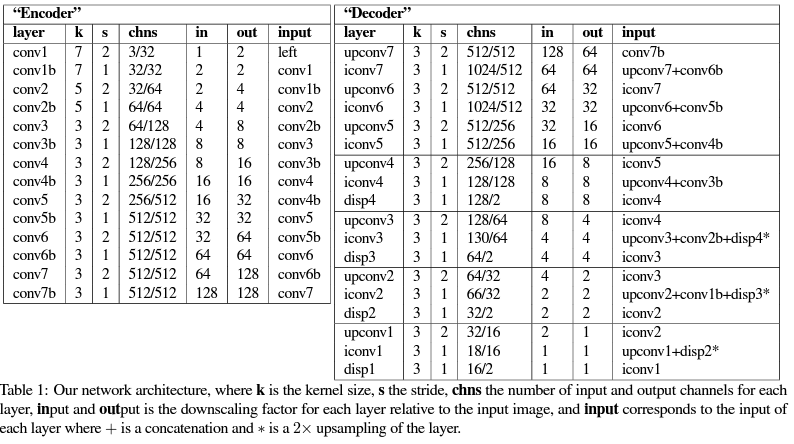
본 논문의 model은 크게 두 부분으로 나뉜다. : encoder (conv1~conv7b) and decoder (upconv7~)
본 논문의 model은 output으로서 disparity \(d^{r}, d^{l}\)을 동시에 추론하는데, 이를 four different output scales에 대해 반복한다.

Train Loss

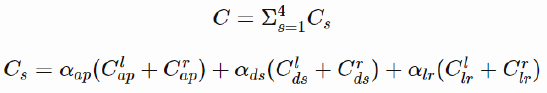
\(C_s\) : loss at output scale s

\(C_{ap}^{l}\) :
appearance matching loss for left image (image reconstruction term)
How much \(I^{r}(d^{l})\) appears similar to \(I^{l}\)

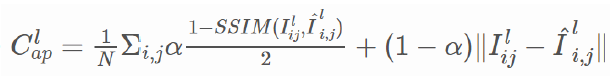
이 때, SSIM (Structural Similarity Index Measure)는 두 images 간의 차이가 작을수록 1 에 가까운 값을 가지며, 정확한 정의는 아래를 참고하자.

\(C_{ds}^{l}\) :
disparity smoothness loss (smoothness term)
How much \(d^{l}\) is smooth

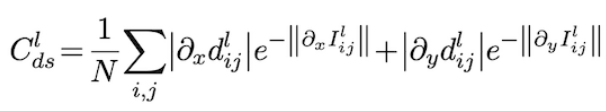
real-world에서 depth가 급격하게 변하는 경우 image boundary 혹은 texture change가 있는 부분이므로 image plane에서도 해당 부분의 image gradient가 크게 나타난다. 따라서 image gradient가 큰 부분에서는 disparity (depth) 변화를 허용하지만, image gradient가 작은 부분에서는 disparity (depth)가 부드럽게 변하도록 하는 것이 disparity smoothness loss의 역할이다.

\(C_{lr}^{l}\) :
left-right consistency (left-right disparity consistency term)
How much \(d^{l}\) and \(d^{r}(d^{l})\) are consistent

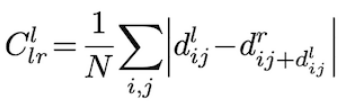
image reconstruction 뿐만 아니라 left-right disparity consistency까지 고려함으로써 depth estimation의 accuracy를 향상시킬 수 있다.

Results & Limitations

Results

Train : on Cityscapes and KITTI 2015 dataset using two different test splits
Test : on other datasets like Make3D and CamVid

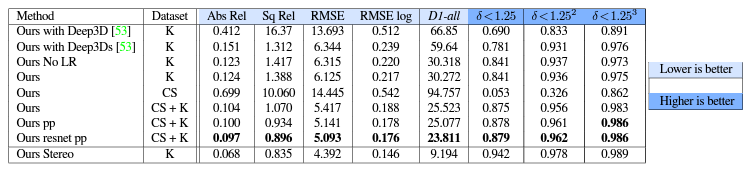
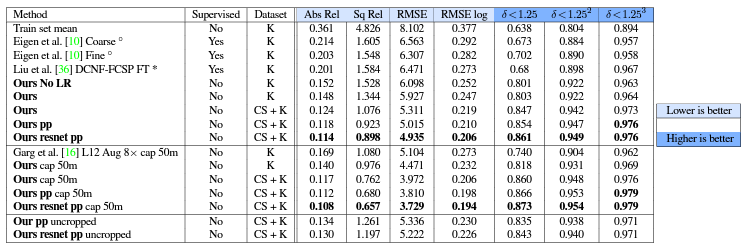
Post-processing :
original left image로부터 구한 disparity map을 \(d^{l}\) 라 하고,
flipped left image로부터 구한 disparity map을 \(d^{l \ast}\) 라 하고,
이를 다시 flip한 걸 \(d^{l \ast \ast}\) 라 할 때,
\(d^{l}\)의 경우 stereo disocclusions which create disparity ramps(경사) on both the left side of the image and the left of occluders 가 있을 수 있는데,
\(d^{l \ast \ast}\)의 경우 disparity ramps are located on the right side of the image and the right of occluders 이므로
We combine both disparity maps to form the final disparity map by assigning the first 5% on the left of the image using \(d^{l \ast \ast}\) and the last 5% on the right to the disparities from \(d^{l}\). The central part of the final disparity map is the average of \(d^{l \ast \ast}\) and \(d^{l}\).
이러한 post-processing을 통해 can reduce the effect of stereo disocclusions, and lead to better accuracy and less visual artifacts,
but double the amount of test time
(stereo disocclusions의 영향을 줄이기 위한 post-processing 과정 아직 완벽하게 이해하지는 못했음)

Limitations

left-right consistency와 post-processing으로 quality 향상을 이룬 건 맞지만, 두 images에서 모두 안 보이는 occlusion region에서의 pixels 때문에 occlusion boundaries에서는 여전히 artifacts가 존재한다. training phase에서 occclusion에 대해 explicitly reasoning하는 것으로 이 문제를 개선할 수는 있지만, supervised methods 또한 모든 pixels에 대해 항상 valid depth를 가지는 것은 아님에 주목할 필요가 있다.
training phase에서 rectified and temporally aligned (image rectification을 거치고 동시에 찍은) stereo image pairs가 필요하다. 이 말은 즉슨, single-view dataset은 training에 쓸 수 없다. (fine-tune하는 것만 가능하다.)
image reconstruction term에 의존한다. 이 말은 즉슨, specular and transparent (거울 같이 반사하는 and 투명한) surfaces에서는 inconsistent depth가 생긴다. 이는 더 정교한 similarity measures를 사용함으로써 개선될 수 있다.

Conclusion

unsupervised mono (single image as input) depth estimation \(\rightarrow\) no need for expensive GT depth
need for binocular stereo image pairs at training
novel loss function : left-right consistency b.w. disparity maps \(\rightarrow\) improve quality of depth map
can generalize to unseen datasets

Future Work

extend to videos (can add temporal consistency)
investigate sparse input as an alternative training signal
(?? 이해 못함)
our model estimates per-pixel depth, but it would be also interesting to predict the full occupancy of the scene
(?? 이해 못함)

중간중간에 있는 질문들은 아직 이해하지 못해서 남겨놓은 코멘트입니다.
추후에 다시 읽어보고 이해했다면 업데이트할 예정입니다.
혹시 알고 계신 분이 있으면 댓글로 남겨주시면 감사하겠습니다!