Normalized Device Coordinates

How NDC Works for Ray

NDC: Normalized Device Coordinates

referenced blog :
https://yconquesty.github.io/blog/ml/nerf/nerf_ndc.html#background

Motivation

NeRF에서
MLP의 input은 3D world-coordinate이고,
MLP의 output인 \(c, \sigma\) 를 accumulate해서 2D pixel-coordinate을 채운다
이 때, LLFF (Local Light Field Fusion) dataset 에 있는
unbounded (in single direction) 3D world-coordinate의 scene 정보를
bounded 3D NDC space로 project하면
MLP를 효율적으로 쓸 수 있다
NDC space로의 projection 과정을 수식적으로 알아보고자 한다.

From world-coordinate To NDC To pixel-coordinate

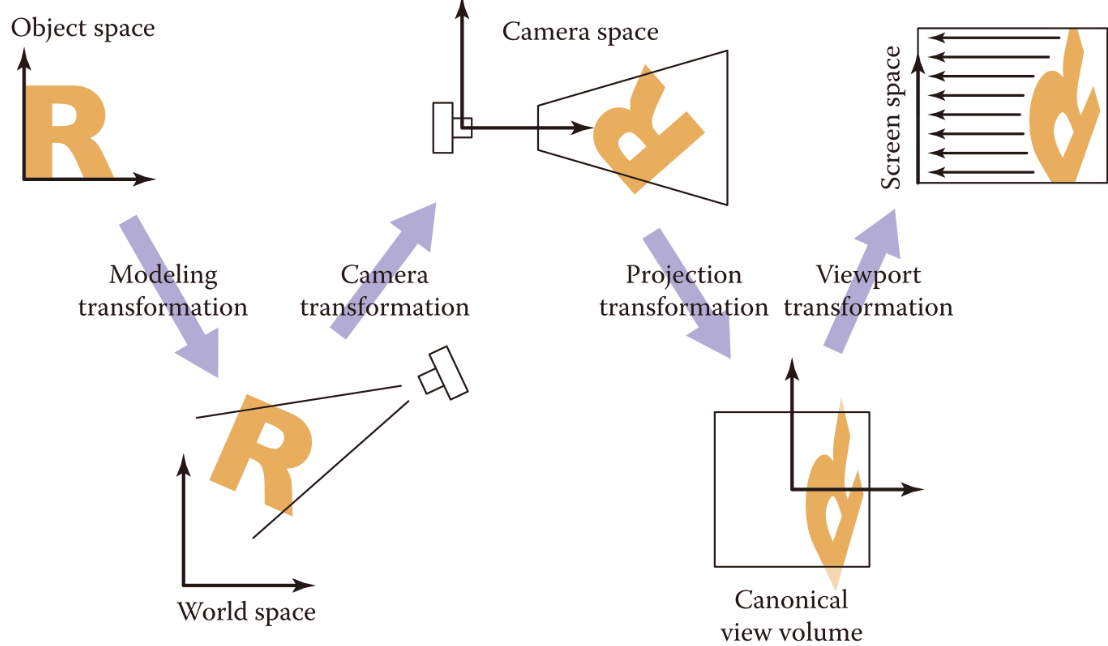
• camera transformation :
  • 3D world-coordinate (canonical-coordinate)
    \(\rightarrow\)
    3D camera-coordinate
  • extrinsic matrix \(\begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix}\)
• projection transformation :
  • 3D camera-coordinate
    \(\rightarrow\)
    3D NDC (normalized-device-coordinate) (canonical view volume)
  • normalized-device-coordinate (NDC) :
    camera 원점이 중앙에 있는 \([-1, 1]^3\) cube (정육면체)
  • frustum \(\rightarrow\) 직육면체 \(\rightarrow\) 정육면체
    consists of perspective projection and then orthographic projection
    z-axis 방향 바꾸기 포함
• viewport transformation :
  • 3D NDC
    \(\rightarrow\)
    2D pixel-coordinate
  • \([-1, 1]^3\) 의 NDC를 flatten하여 2 \(\times\) 2 square를 raster image로 mapping
  • intrinsic matrix \(\begin{bmatrix} f_x & s & W/2 \\ 0 & f_y & H/2 \\ 0 & 0 & 1 \end{bmatrix}\) (초점거리 곱하고 원점 좌상단 이동)
    y-axis 방향 바꾸기 포함

Projection Transformation

Step 1. Perspective Projection

• frustum을 bounded cuboid로 변환
  bound :
  \(x \in [l, r]\) where \(l \lt 0\), \(r \gt 0\)
  \(y \in [b, t]\) where \(b \lt 0\), \(t \gt 0\)
  \(z \in [f, n]\) where \(f \lt 0\), \(n \lt 0\)

3D camera-coordinate

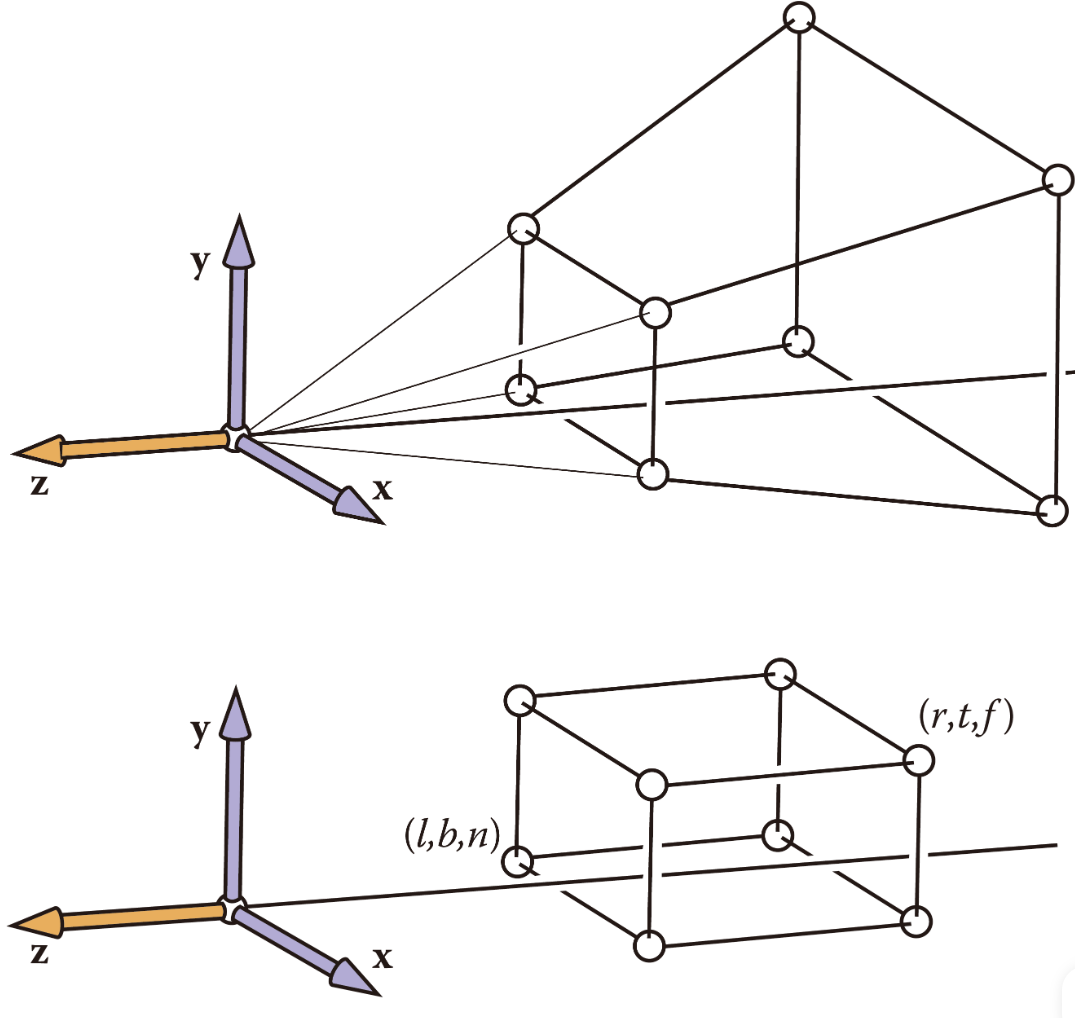
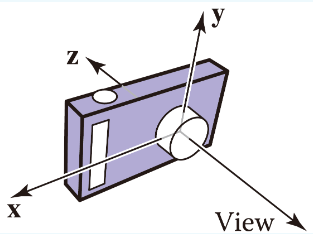
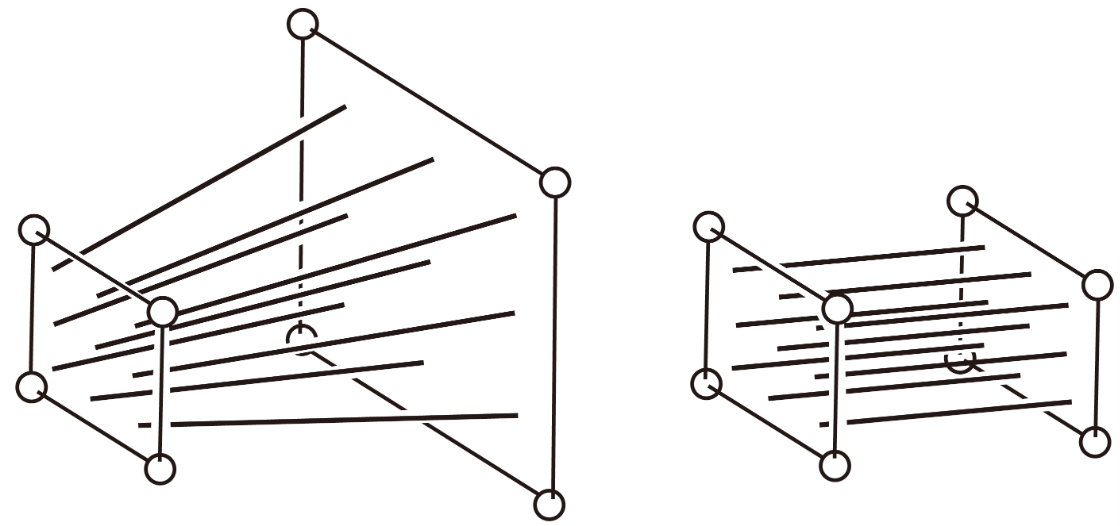
• \(z = n\) plane은 그대로 냅두고, 직육면체 꼴이 되도록 그 뒤 plane 변환
  camera를 통과하는 any line은 z-axis에 평행한 line이 됨

• perspective projection matrix :
  \(P_{per} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{bmatrix}\)
  \(P_{per} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} = \begin{bmatrix} nX \\ nY \\ (n+f)Z - nf \\ Z \end{bmatrix}\)
  ?????

Step 2. Orthographic Projection

• corner (l, b, n)이 원점이 되도록 shift한 뒤,
  \([0, r-l] \times [0, t-b] \times [f-n, 0]\) 의 직육면체를 \([0, 2] \times [0, 2] \times [-2, 0]\) 의 정육면체로 scale한 뒤,
  center (1, 1, -1)이 원점이 되도록 \([-1, 1]^3\) 으로 shift

• orthographic projection matrix :
  \(M_{orth} = \begin{pmatrix} I_{3 \times 3} & \begin{matrix} -1 \\ -1 \\ 1 \end{matrix} \\ 0_{1 \times 3} & 1 \end{pmatrix} \begin{pmatrix} \begin{matrix} \frac{2}{r-l} & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 \\ 0 & 0 & \frac{2}{n-f} \end{matrix} & 0_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{pmatrix} \begin{pmatrix} I_{3 \times 3} & \begin{matrix} -l \\ -b \\ -n \end{matrix} \\ 0_{1 \times 3} & 1 \end{pmatrix}\)
  \(= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{bmatrix}\)

Step 3. Projection Matrix

Since perspective projection matrix is scalable,
\(M_{proj} = M_{orth} (- P_{per})\)
\(= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} -n & 0 & 0 & 0 \\ 0 & -n & 0 & 0 \\ 0 & 0 & -n-f & nf \\ 0 & 0 & -1 & 0 \end{bmatrix}\)
\(= \begin{bmatrix} -\frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & -\frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{n+f}{n-f} & \frac{2nf}{n-f} \\ 0 & 0 & -1 & 0 \end{bmatrix}\)

camera-coordinate에서 \(z \in [f, n]\) where \(f \lt 0\), \(n \lt 0\) 이었는데,
NDC에서는 z-axis의 방향이 반대이므로
\(f \lt 0\), \(n \lt 0\) 대신 \(f = -f \gt 0\), \(n = -n \gt 0\) 를 대입하면,
\(M_{proj} = \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{n+f}{n-f} & -\frac{2nf}{n-f} \\ 0 & 0 & -1 & 0 \end{bmatrix}\)

OpenGL과 같은 graphics frameworks에서는 보통
\(M_{proj}X\) 를 \(M_{proj}X\) 의 fourth entry로 나눴을 때 \(M_{proj}X\) 의 third entry(Z 값)이 양수가 되도록 하기 때문에 (아래 Step 4의 NDC 참고)
조금 수정하면
최종적인 projection matrix는
\(M_{proj} = \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & -\frac{n+f}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \end{bmatrix}\)

camera frustum은 보통 symmetric하므로 \(l = -r\), \(b = -t\) 라 했을 때
projection matrix는
\(M_{proj} = \begin{bmatrix} \frac{n}{r} & 0 & 0 & 0 \\ 0 & \frac{n}{t} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & -\frac{2nf}{f-n} \\ 0 & 0 & -1 & 0 \end{bmatrix}\)

Step 4. from camera-coordinate to NDC

• camera-coordinate :
  \(\boldsymbol X = \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}\)
  where \(Z \lt 0\)

• NDC :

  • \(\begin{bmatrix} -\frac{n}{r}\frac{X}{Z} \\ -\frac{n}{t}\frac{Y}{Z} \\ \frac{f+n}{f-n} + \frac{2nf}{f-n}\frac{1}{Z} \\ 1 \end{bmatrix} = \boldsymbol x \sim M_{proj} \boldsymbol X = \begin{bmatrix} \frac{n}{r}X \\ \frac{n}{t}Y \\ -\frac{f+n}{f-n}Z -\frac{2nf}{f-n} \\ -Z \end{bmatrix}\)
    where \(Z \lt 0\) and \(n, f \gt 0\)
  • 검토해보면, \(Z = -n\) 은 \(x_Z = -1\) 로 mapping되고, \(Z = -f\) 는 \(x_Z = 1\) 로 잘 mapping되네~
  • Let
    \(a_x = -\frac{n}{r}\)
    \(a_y = -\frac{n}{t}\)
    \(a_z = \frac{f+n}{f-n}\)
    \(b_z = \frac{2nf}{f-n}\)
    Then \(\boldsymbol x = \begin{bmatrix} a_x\frac{X}{Z} \\ a_y\frac{Y}{Z} \\ a_z + \frac{b_z}{Z} \\ 1 \end{bmatrix} = \begin{bmatrix} a_x\frac{X}{Z} \\ a_y\frac{Y}{Z} \\ a_z + \frac{b_z}{Z} \end{bmatrix}\)

Linear in Disparity

• 출처 : https://charlieppark.kr

• LLFF (Local Light Field Fusion) :
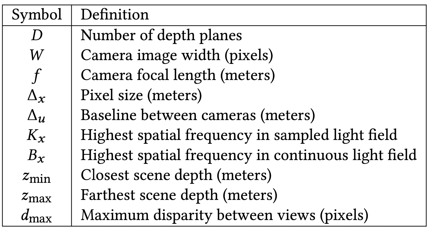
  • Nyquist-rate에 따르면 카메라가 \(\frac{1}{2K_xf(\frac{1}{z_{min}}-\frac{1}{z_{max}})}\) 보다 촘촘히 있어야 한다
    \(\Delta_{u} \leq \frac{1}{2K_xf(\frac{1}{z_{min}}-\frac{1}{z_{max}})}\)
    where \(K_x = \text{min}(B_x, \frac{1}{2\Delta_{x})\)
  • LLFF dataset에서 다루는 scene은 unbounded in single direction (front-facing) 이므로 \(z_{max} = \infty\) 이므로
    \(\Delta_{u} \leq \frac{1}{2K_xf\frac{1}{z_{min}}}\)
  • 즉, \(z_{min}\) 이 작을수록 (물체가 가까이 있을수록)
    더 촘촘한 view-sampling이 필요하며
    high-freq. detail을 많이 가지고 있다는 의미이다
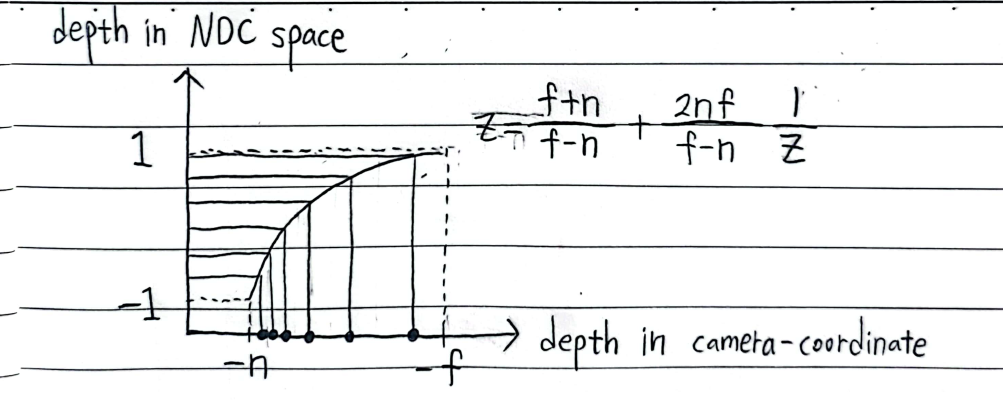
• \(\begin{bmatrix} -\frac{n}{r}\frac{X}{Z} \\ -\frac{n}{t}\frac{Y}{Z} \\ \frac{f+n}{f-n} + \frac{2nf}{f-n}\frac{1}{Z} \\ 1 \end{bmatrix} = \boldsymbol x \sim M_{proj} \boldsymbol X = \begin{bmatrix} \frac{n}{r}X \\ \frac{n}{t}Y \\ -\frac{f+n}{f-n}Z -\frac{2nf}{f-n} \\ -Z \end{bmatrix}\)
  where \(Z \lt 0\) and \(n, f \gt 0\) 에서
  \(Z\) 축에 해당하는 \(\frac{f+n}{f-n} + \frac{2nf}{f-n}\frac{1}{Z}\) 만 보면
  NDC space의 깊이 값은 원래 camera coordinate의 깊이 값의 역수, 즉 camera-coordinate의 disparity에 비례한다는 것을 알 수 있다
  즉, NDC space에서의 depth distance에 따라 stratified uniform sampling한다면
  원래 camera coordinate의 disparity에 비례하여 sampling하는 효과를 가진다

Projection in NeRF ray

any 3D points on ray \(r = o + td\)를
NDC space (camera 원점이 중앙에 있는 \([-1, 1]^3\) cube) 로 projection하면
3D points on projected ray \(r^{\ast} = o^{\ast} + t^{\ast} d^{\ast}\) 가 된다
위에서 유도한 Projection Matrix 를 사용하면
\(\boldsymbol x = \begin{bmatrix} a_x\frac{o_x + td_x}{o_z + td_z} \\ a_y\frac{o_y + td_y}{o_z + td_z} \\ a_z + \frac{b_z}{o_z + td_z} \end{bmatrix} = \begin{bmatrix} o_x^{\ast} + t^{\ast} d_x^{\ast} \\ o_y^{\ast} + t^{\ast} d_y^{\ast} \\ o_z^{\ast} + t^{\ast} d_z^{\ast} \end{bmatrix}\)

먼저 projected 원점 좌표를 구해보자
\(t = t^{\ast} = 0\) 를 대입하면
\(o^{\ast} = \begin{bmatrix} o_x^{\ast} \\ o_y^{\ast} \\ o_z^{\ast} \end{bmatrix} = \begin{bmatrix} a_x\frac{o_x}{o_z} \\ a_y\frac{o_y}{o_z} \\ a_z + \frac{b_z}{o_z} \end{bmatrix}\)

다음으로 projected t와 d를 구해보자
\(\begin{bmatrix} t^{\ast} d_x^{\ast} \\ t^{\ast} d_y^{\ast} \\ t^{\ast} d_z^{\ast} \end{bmatrix} = \begin{bmatrix} a_x\frac{o_x + td_x}{o_z + td_z} \\ a_y\frac{o_y + td_y}{o_z + td_z} \\ a_z + \frac{b_z}{o_z + td_z} \end{bmatrix} - \begin{bmatrix} o_x^{\ast} \\ o_y^{\ast} \\ o_z^{\ast} \end{bmatrix}\)
\(= \begin{bmatrix} a_x\frac{o_x + td_x}{o_z + td_z} - a_x\frac{o_x}{o_z} \\ a_y\frac{o_y + td_y}{o_z + td_z} - a_y\frac{o_y}{o_z} \\ a_z + \frac{b_z}{o_z + td_z} - (a_z + \frac{b_z}{o_z}) \end{bmatrix}\)
\(= \begin{bmatrix} a_x\frac{td_z}{o_z + td_z}(\frac{d_x}{d_z} - \frac{o_x}{o_z}) \\ a_y\frac{td_z}{o_z + td_z}(\frac{d_y}{d_z} - \frac{o_y}{o_z}) \\ -b_z\frac{td_z}{o_z + td_z}\frac{1}{o_z} \end{bmatrix}\)
\(= \frac{td_z}{o_z + td_z} \begin{bmatrix} a_x(\frac{d_x}{d_z} - \frac{o_x}{o_z}) \\ a_y(\frac{d_y}{d_z} - \frac{o_y}{o_z}) \\ -b_z\frac{1}{o_z} \end{bmatrix}\)

Result

ray \(r = o + td\)를
NDC space (camera 원점이 중앙에 있는 \([-1, 1]^3\) cube) 로 projection 했을 때
projected ray \(r^{\ast} = o^{\ast} + t^{\ast} d^{\ast}\) 는 아래와 같이 구할 수 있다

\(o^{\ast} = \begin{bmatrix} o_x^{\ast} \\ o_y^{\ast} \\ o_z^{\ast} \end{bmatrix} = \begin{bmatrix} a_x\frac{o_x}{o_z} \\ a_y\frac{o_y}{o_z} \\ a_z + \frac{b_z}{o_z} \end{bmatrix}\)
and
\(t^{\ast} = \frac{td_z}{o_z + td_z} = 1 - \frac{o_z}{o_z + td_z}\)
and
\(d^{\ast} = \begin{bmatrix} d_x^{\ast} \\ d_y^{\ast} \\ d_z^{\ast} \end{bmatrix} = \begin{bmatrix} a_x(\frac{d_x}{d_z} - \frac{o_x}{o_z}) \\ a_y(\frac{d_y}{d_z} - \frac{o_y}{o_z}) \\ -b_z\frac{1}{o_z} \end{bmatrix}\)

Ray Projection to NDC 장점

• ray에서 \(t \in [0, \infty)\) 였다면 projected ray에서 \(t^{\ast} \in [0, 1)\)
  LLFF dataset에서
  camera에서 출발한 ray가 아무 object도 “hit”하지 않는다면 \(t = \infty\)일텐데,
  NDC (bounded cube)로 warp한다면 \(t^{\ast} \in [0, 1)\) 이므로
  MLP 효율적으로 쓸 수 있음

• single-direction이긴 하지만
  NDC space에서의 depth distance에 따라 stratified uniform sampling한다면
  원래 camera coordinate의 disparity에 비례하여 sampling하는 효과를 가지므로
  가까이 있는 content는 많이 sampling하고 멀리 있는 content는 덜 sampling함으로써
  임의의 scale의 unbounded scene을 잘 다룰 수 있음

Projection transformation 한계

LLFF dataset과 같이 single direction으로만 unbounded된 camera frustum, 즉 front-facing scene에 대해서만 적용 가능하고
unbounded 360 scene에 대해서는 기본 NeRF가 잘 수행 못함
\(\rightarrow\) MipNeRF360 등 NeRF 후속 연구에서 해결됨

특정 case

\(f_{cam}\)이 camera의 focal length이고,
\(W, H\)가 image plane의 width, height in pix 일 때
image plane이 정확히 camera frustum의 near plane에 있고
camera frustum의 far plane을 infinity로 확장하도록
camera를 설정하면,
\(z = -n = -f_{cam} \lt 0\), \(r = \frac{W}{2}\), \(t = \frac{H}{2}\), \(z = -f \rightarrow -\infty\) 이므로

\(a_x = -\frac{n}{r} = -\frac{f_{cam}}{\frac{W}{2}}\)
\(a_y = -\frac{n}{t} = -\frac{f_{cam}}{\frac{H}{2}}\)
\(\lim_{f \rightarrow \infty} a_z = \lim_{f \rightarrow \infty} \frac{f+n}{f-n} = 1\)
\(\lim_{f \rightarrow \infty} b_z = \lim_{f \rightarrow \infty} \frac{2nf}{f-n} = 2n\)
이므로

ray \(r = o + td\) 를 NDC로 projection했을 때
projected ray \(r^{\ast} = o^{\ast} + t^{\ast} d^{\ast}\) 에서
\(o^{\ast} = \begin{bmatrix} -\frac{f_{cam}}{\frac{W}{2}}\frac{o_x}{o_z} \\ -\frac{f_{cam}}{\frac{H}{2}}\frac{o_y}{o_z} \\ 1 + \frac{2n}{o_z} \end{bmatrix}\)
and
\(t^{\ast} = \frac{td_z}{o_z + td_z} = 1 - \frac{o_z}{o_z + td_z}\)
and
\(d^{\ast} = \begin{bmatrix} -\frac{f_{cam}}{\frac{W}{2}}(\frac{d_x}{d_z} - \frac{o_x}{o_z}) \\ -\frac{f_{cam}}{\frac{H}{2}}(\frac{d_y}{d_z} - \frac{o_y}{o_z}) \\ -2n\frac{1}{o_z} \end{bmatrix}\)

NDC projection in NeRF Pytorch code

NeRF-Pytorch 기준으로
run_nerf_helpers.py의 ndc_rays()에 구현되어 있으며
자세한 설명은 NeRF-Code-Review에 있음