Neuralangelo (and InstantNGP)

High-Fidelity Neural Surface Reconstruction (CVPR 2023)

Neuralangelo - High-Fidelity Neural Surface Reconstruction (CVPR 2023)

Zhaoshuo Li, Thomas Müller, Alex Evans, Russell H. Taylor, Mathias Unberath, Ming-Yu Liu, Chen-Hsuan Lin

paper :
https://arxiv.org/pdf/2306.03092
project website :
https://research.nvidia.com/labs/dir/neuralangelo/
code :
https://github.com/nvlabs/neuralangelo
reference :
NeRF and 3DGS Study

Abstract

• multi-resolution hash grid representation
  with SDF-based volume rendering
  (3D surface recon.)

• no need for auxiliary data like segmentation or depth

• Novelty :

  • numerical gradient (backpropagation locality 문제 해결)
  • coarse-to-fine (점점 high resol.)

Related Works

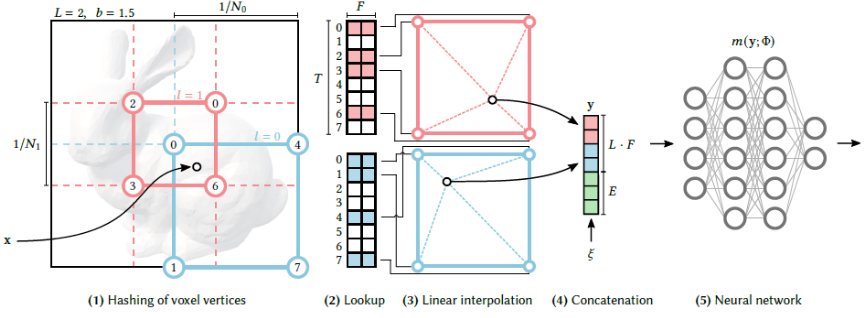
• Instant NGP [1] Link :
  모든 좌표(pixel) 각각에 대해 deep MLP output을 구하면 연산량이 너무 크므로
  연산량 감소 및 speed-up 위해
  Hash Grid(연산량 감소)와 Linear Interpolation(continuous 보장)을 이용한
  좌표 encoding 기법 제시
  • STEP 1)
    \(d\)-dim. scene일 때
    input 좌표 \(x\) 가 주어졌을 때
    grid level별로 주위 \(2^d\)-개 좌표 선택
    • multi-resolution (grid-level \(l\)) :
      \(N_l = \lfloor N_{min} \cdot b^l \rfloor\)
      where \(b = e^{\frac{\text{ln} N_{max} - \text{ln} N_{min}}{L-1}}\)
      MLP size가 작더라도 multi-resol. 덕분에 high approx. power 가짐
    • 주위 좌표 선택 :
      \(N_l\) 만큼 scale된 좌표 계산
      \(\lfloor x_l \rfloor = \lfloor x \cdot N_l \rfloor\)
      \(\lceil x_l \rceil = \lceil x \cdot N_l \rceil\)
  • STEP 2)
    선택한 각 좌표에 대해 HashKey를 계산한 뒤 HashTable에서 Value 읽어옴
    • HashKey :
      grid-level 마다 1개씩 HashTable이 정의되며
      Spatial Hash Function(2003)에 의해
      HashKey \(h(x) = (\text{XOR}_{i=1}^{d} x_i \pi_{i})\ \text{mod}\ T \in [0, T-1]\)
      where \(d\) : dim., \(\pi\) : dim.마다 임의로 정해둔 constant, \(T\) : Hash Table Size
    • HashValue :
      \(T \times F\) 의 HashTable로부터 \(F\)-dim. feature vector인 HashValue를 얻음
  • STEP 3)
    주위 좌표까지의 거리를 기반으로
    HashValue들을 Linear Interpolation(weighted sum)하여
    grid-level 별로 1개의 feature vector로 만듬
  • STEP 4)
    각 grid-level 별 feature vectors와 auxiliary 값(e.g. view direction)을 concat하여
    최종 feature vector 만듬
  • STEP 5)
    shallow MLP 통과
  • STEP 6)
    Backpropagation :
    MLP weight와 Hash Table의 Value(\(F\)-dim. feature vector) 업데이트

Numerical Gradient

• Gradient :
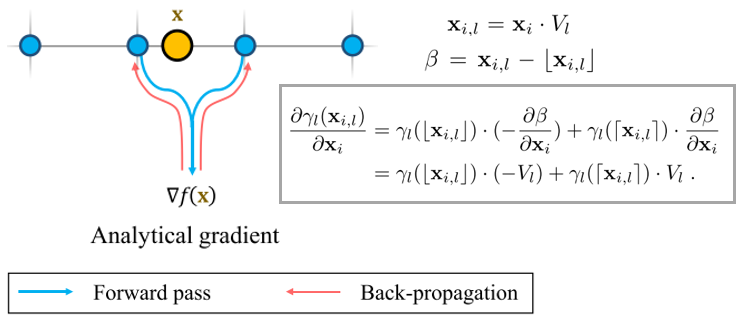
  • analytical gradient : \(\nabla f(x_i) = \frac{\partial f(x_i)}{\partial x_i}\)
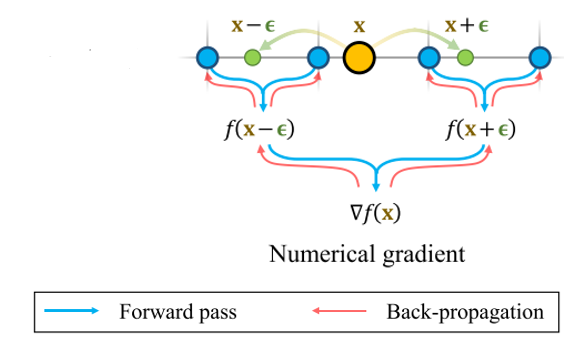
  • numerical gradient : \(\text{lim}_{\epsilon_{x} \rightarrow 0} \frac{f(x_i + \epsilon_{x}) - f(x_i - \epsilon_{x})}{2\epsilon_{x}}\)

Analytical Graident

Numerical Gradient

• Instant NGP [1] 에서처럼
  input coordinate encode하기 위해
  multi-resolution hash grid representation 사용
  • 문제 :
    SDF-based volume rendering에 multi-resolution hash grid를 직접적으로 적용하면
    large smooth regions의 surface에 noise 및 hole이 생김
  • 이유 :
    • surface recon.에서 RGB(color) 및 SDF(geometry)를 MLP output으로 얻는데
      surface regularization loss를 구할 때 higher-order derivatives of SDF 계산해야 함
      • first-order derivative of SDF \(f(x_i)\) :
        Eikonal constraints on the surface normals 계산
        \(L_{eik} = \frac{1}{N} \sum_{i=1}^N (\| \nabla f(x_i) \| - 1)^2\)
      • second-order derivative of SDF \(f(x_i)\) :
        surface curvatures 계산
        \(L_{curv} = \frac{1}{N} \sum_{i=1}^N | \nabla^{2} f(x_i) |\)
    • 그리고 이러한 SDF의 higher-order derivatives 계산하기 위해
      analytical gradient \(\nabla f(x_i) = \frac{\partial f(x_i)}{\partial x_i}\) 사용
    • 근데, analytical gradient 사용하면
      only backpropagate to local cell의 HashValues
      (locality 문제 발생!)
    • 특히 recon.할 surface가 multiple grid cells에 걸쳐 있을 경우
      analytical gradient를 사용하면
      adjacent cells는 업데이트 안 됨

Fig a. Analytical Gradient from local cell

• Instant NGP [1] 에서처럼
  input coordinate encode하기 위해
  multi-resolution hash grid representation 사용
  • 해결 :
    • SDF의 higher-order derivatives 계산하기 위해
      numerical gradient \(\text{lim}_{\epsilon \rightarrow 0} \frac{f(x_i + \epsilon) - f(x_i - \epsilon)}{2\epsilon}\) 사용
    • forward pass에서 rendering하기 위해 (recon. loss 구하기 위해) SDF 계산할 때는
      sampled point 1개만 사용
    • regularization loss 구하기 위해 SDF의 higher-order derivatives 계산할 때는
      adjacent cells의 SDF까지 이용하는 numerical gradient를 사용함으로써
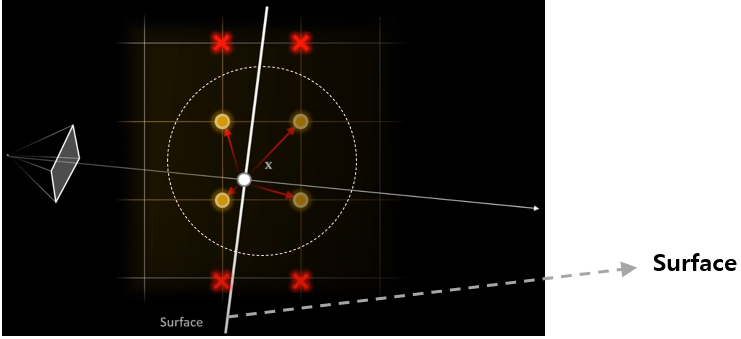
      backward pass에서 backpropagate to adjacent cells
    • adjacent 6개의 cells \(x_i \pm \epsilon\) 각각에 대해 trilinear sampling으로 SDF 값 계산하고
      그 차이를 이용해서 numerical gradient 계산
      이는 backward pass에 이용
    • local cell \(x_i\) 로만 backpropagate하는 게 아니라
      주위 6개의 cells \(x_i \pm \epsilon\) 으로 backpropagate하므로
      smoothing on SDF 역할 수행

Fig b. Numerical Gradient from adjacent cells

Coarse-to-Fine

• Coarse-to-Fine :
  점점 hash grid encoding resol. \(N_l\) 증가시키고
  이에 맞춰서 numerical gradient의 step size \(\epsilon\) 감소시킴

Code

• .yaml 로부터 config Dictionary 만들기 Code

• .yaml에 적어놓은 module을 동적으로 읽어와서 해당 module 내 class 사용하기 Code

• Train 껍질 Code

• Trainer Code \(\rightarrow\) overriding \(\rightarrow\) Code

• 각종 함수 계산하는 utils Code

Question

• Q1 :
  analytical gradient에 비해 numerical gradient가 갖는 장점을 정리해서 알려주세요

• A1 :
  • numerical gradient는
    point 하나만 sampling해도
    그 주위의 여러 samples’ feature까지 다룰 수 있음
  • gradient 하나가 얼마나 넓은 범위에 영향을 미치는지에 따라 sample efficiency가 결정되고 학습의 효율성이 결정됨
    continuous surface 상황에서는 하나의 error에서 나오는 gradient가 여러 군데에 영향을 동시에 미치는 것이 적합함
    사실 forward pass에서 많은 points를 aggregate(또는 blur)하면 analytical gradient로도 backpropagation이 여러 군데에 퍼지게 할 수 있다
    하지만 그러면 forward 쪽이 blur해지면서 frequency bound가 생기고, 속도가 느려짐
    따라서 forward pass 쪽은 건들지 않고 backward pass 쪽만 건드려서 (numerical gradient for regularization loss)
    backpropagation이 여러 군데에 퍼지게 함

• Q2 :
  analytical gradient 대신 numerical gradient 쓰기 위해 adjacent cells’ SDF까지 계산하려면 performance 상승하긴 하지만 느려지지 않나요?

• A2 :
  Instant-NGP의 Hash Grid 방식 자체가 빨라서 ㄱㅊ
  내 피셜로는 regularization loss 구할 때만 adjacent cells’ SDF 이용하므로 inference rendering speed는 그대로라서 training speed 저하 미비