EE534 Pattern Recognition Midterm

Lecture Summary (24F)

Lecture :
24F EE534 Pattern Recognition
by KAIST Munchurl Kim VICLab

Chapter 1. Overview

Discriminative vs Generative

• Discriminative model :
  • learn posterior directly
  • e.g. logistic regression, SVM, nearest neighbor, CRF, Decision Tree and Random Forest, traditional NN
• Generative model :
  • learn likelihood and prior to maximize posterior
  • e.g. Bayesian network, Autoregressive model, GAN, Diffuson model

Chapter 2. Bayes Decision Theory

Bayes Decision Rule

• conditional probability density :
  Let \(w\) be state (class)
  Let \(x\) be data (continous-valued sample)
  • prior : \(P(w=w_k)\)

  • likelihood : PDF $$P(x

    w_k)$$

  • posterior : $$P(w_k	x) = \frac{P(x	w_k)P(w_k)}{P(x)}$$ (Bayes Rule)
    where $$P(w_1	x) + P(w_2	x) + \cdots + P(w_N	x) = 1$$

  • evidence : $$P(x) = \sum_{k=1}^N P(x

    w_k)P(w_k) = \sum_{k=1}^N P(x, w_k)$$

• Bayes Decision Rule :
  posterior 더 큰 쪽 고름!
  • Two-class (\(w_1, w_2\)) problem :
    choose \(w_1\)
    if \(P(w_1 | x) \gt P(w_2 | x)\)
    if \(P(x|w_1)P(w_1) \gt P(x|w_2)P(w_2)\)
    if \(\frac{P(x|w_1)}{P(x|w_2)} \gt \frac{P(w_2)}{P(w_1)}\)
    (likehood ratio \(\gt\) threshold)
  • multi-class problem :
    choose \(w_i\) where \(P(w_i | x)\) is the largest

minimum error

• minimum error :
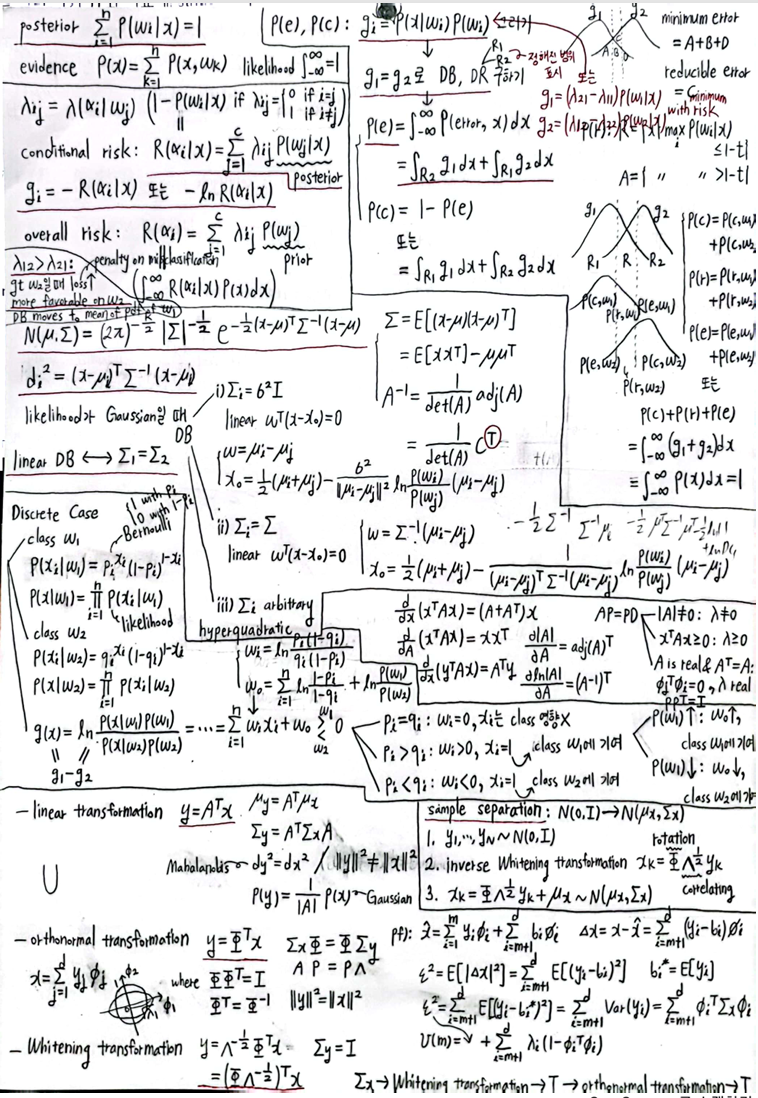
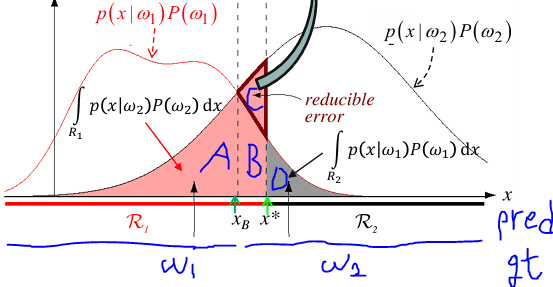
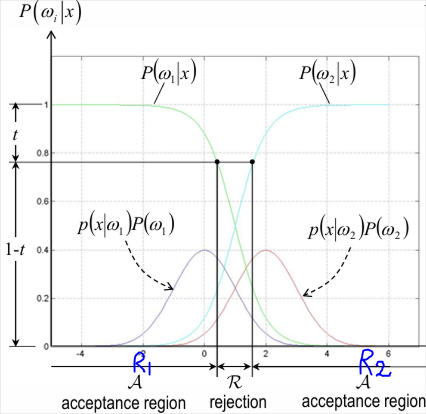
  GT가 \(w_1, w_2\) 이고, Predicted가 \(R_1, R_2\) 일 때,
  • \(P(error) = \int_{-\infty}^{\infty} P(error, x)dx = \int_{-\infty}^{\infty} P(error|x)P(x)dx\)
    \(= \int_{R_2}P(w_1|x)P(x)dx + \int_{R_1}P(w_2|x)P(x)dx\)
    \(= \int_{R_2}P(x|w_1)P(w_1)dx + \int_{R_1}P(x|w_2)P(w_2)dx\)
    \(= \begin{cases} A+B+D & \text{if} & x_B \\ A+B+C+D & \text{if} & x^{\ast} \end{cases}\)
    where \(A+B+D\) is minimum error and \(C\) is reducible error
    (아래 그림 참고)
  • \(P(correct)\)
    \(= \int \text{max}_{i} P(x|w_i)P(w_i)dx = \int_{R_1}P(x|w_1)P(w_1)dx + \int_{R_2}P(x|w_2)P(w_2)dx\)
  • \(P(error) = 1 - P(correct)\)
    \(= 1 - \int \text{max}_{i} P(x|w_i)P(w_i)dx = \int_{R_2}P(x|w_1)P(w_1)dx + \int_{R_1}P(x|w_2)P(w_2)dx\)
    since \(\int_{-\infty}^{\infty} P(x|w_1)P(w_1)dx + \int_{-\infty}^{\infty} P(x|w_2)P(w_2)dx = 1\)
    (\(\int_{-\infty}^{\infty} P(x|w_1)P(w_1)dx \neq 1\) 임에 주의!)

• minimum error with rejection :
  decision이 확실하지 않을 때는 classification 자체를 reject하는 게 적절
  (classification error도 줄어들고, correct classification도 줄어듬)
  • feature space \(x\) 를 rejection region \(R\) 과 acceptance region \(A\) 으로 나눠서
    rejection region \(R=\{ x | \text{max}_{i} P(w_i | x) \leq 1 - t\}\) 에서는 reject decision
    acceptance region \(A=\{ x | \text{max}_{i} P(w_i | x) \gt 1 - t\}\) 에서는 \(w_1\) or \(w_2\) 로 classification decision 수행
  • \(P_c(t) = P(correct)\)
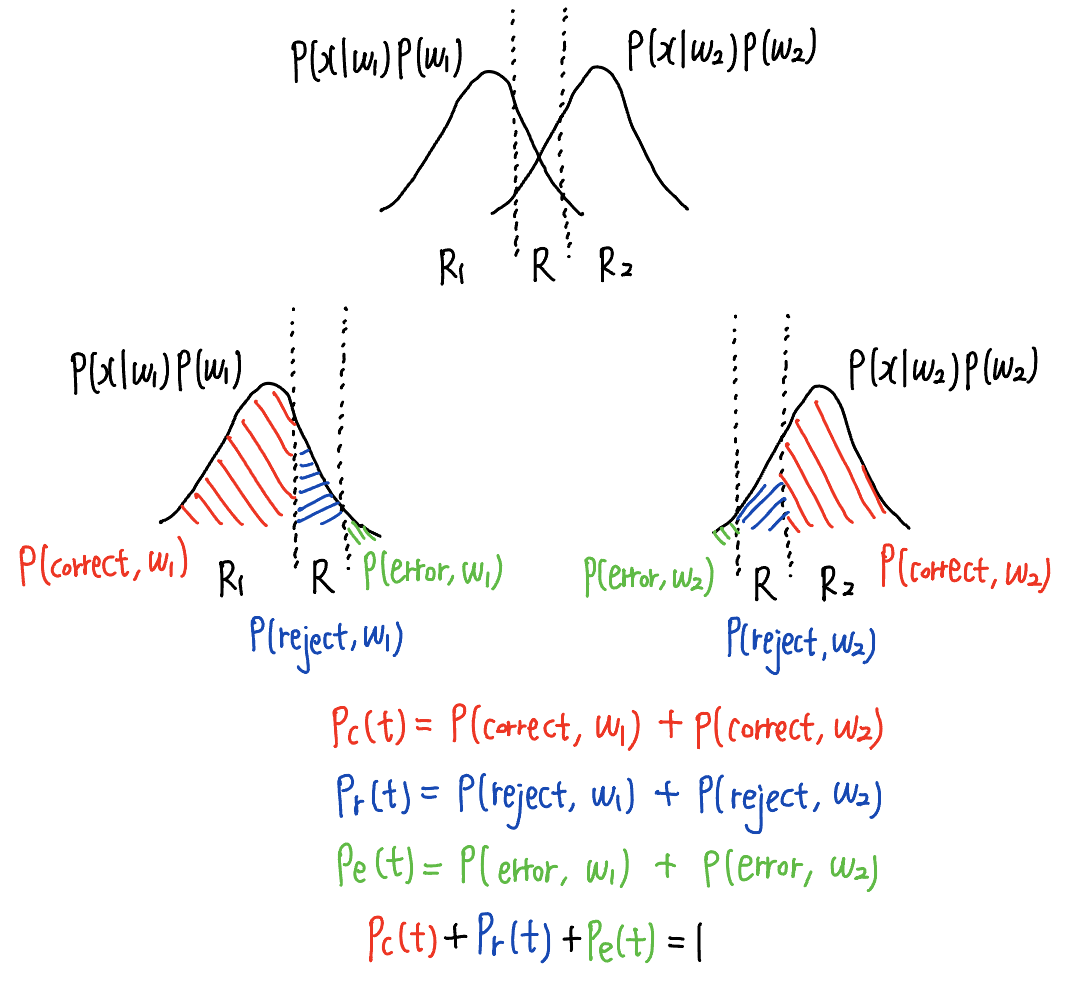
    \(= \int_{A} \text{max}_{i} P(x|w_i)P(w_i)dx = \int_{R_1}P(x|w_1)P(w_1)dx + \int_{R_2}P(x|w_2)P(w_2)dx\)
  • \(P_r(t) = P(reject)\)
    \(= \int_{R}P(x|w_1)P(w_1)dx + \int_{R}P(x|w_2)P(w_2)dx\)
    \(= \int_{R} P(x)dx\)
  • \(P_e(t) = P(error)\)
    \(= P(error, w_1) + P(error, w_2)\)
    \(= 1 - P_r(t) - P_c(t)\) by 아래 식 대입
    where \(P(error, w_1) = \int_{-\infty}^{\infty} P(x|w_1)P(w_1)dx - P(reject, w_1) - P(correct, w_1)\)
    where \(P(error, w_2) = \int_{-\infty}^{\infty} P(x|w_2)P(w_2)dx - P(reject, w_2) - P(correct, w_2)\)
    where \(\int_{-\infty}^{\infty} P(x|w_1)P(w_1)dx + \int_{-\infty}^{\infty} P(x|w_2)P(w_2)dx = \int_{-\infty}^{\infty} P(x)dx = 1\)
• Summary :

  • $$P(w_{i}

    x)$$ : rejection/acceptance region 구하는 데 사용

  • \(P(x|w_i)P(w_i)\) : \(P(correct, w_i), P(reject, w_i), P(error, w_i)\) 구해서
    \(P_c(t), P_r(t), P_e(t)\) 구하는 데 사용
  • \[P_c(t) + P_r(t) + P_e(t) = 1\]

Bayes Decision Rule w. Bayes risk

• Bayes risk (minimum overall risk) :
  \(\Omega = \{ w_1, \cdots w_c \}\) 에서 \(w_j\) 는 \(j\) -th class
  \(A = \{ \alpha_{1}, \cdots, \alpha_{c} \}\) 에서 \(\alpha_{i}\) 는 class \(w_i\) 라고 예측하는 action
  \(\lambda(\alpha_{i} | w_j) = \lambda_{ij}\) : class \(w_j\) 가 GT일 때, class \(w_i\) 로 pred. 했을 때의 loss
  • conditional risk for taking action \(\alpha_{i}\) :
    특정 input \(x\) 에 대해
    \(R(\alpha_{i}|x) = \sum_{j=1}^c \lambda(\alpha_{i}|w_j)P(w_j|x)\)
  • overall risk for taking action \(\alpha_{i}\) :
    모든 input \(x\) 에 대해 적분
    \(R(\alpha_{i}) = \int R(\alpha_{i}|x)P(x)dx\)
    \(= \int \sum_{j=1}^c \lambda(\alpha_{i}|w_j)P(w_j|x) P(x)dx\)
    \(= \sum_{j=1}^c \lambda(\alpha_{i}|w_j)P(w_j) \int P(x|w_j)dx\)
    \(= \sum_{j=1}^c \lambda(\alpha_{i}|w_j)P(w_j)\)
    \(= \sum_{j=1}^c \lambda_{ij}P(w_j)\)
    where pdf(likelihood) 합 \(\int P(x|w_j)dx = 1\)
  • 모든 input \(x\) 에 대해 가장 loss가 최소인 class \(w_i\) 로 예측하면,
    minimum overall risk (= Bayes risk) 를 가짐
• Bayes Decision Rule for Bayes risk :
  • Two-class (\(w_1, w_2\)) problem :
    choose \(w_1\)
    if \(R(\alpha_{1} | x) \lt R(\alpha_{2} | x)\)
    if \(\lambda_{11}P(w_1 | x) + \lambda_{12}P(w_2 | x) \lt \lambda_{21}P(w_1 | x) + \lambda_{22}P(w_2 | x)\)
    if \((\lambda_{21} - \lambda_{11})P(w_1 | x) \gt (\lambda_{12} - \lambda_{22})P(w_2 | x)\)
    if \(\frac{P(x | w_1)}{P(x | w_2)} \gt \frac{(\lambda_{12} - \lambda_{22})P(w_2)}{(\lambda_{21} - \lambda_{11})P(w_1)}\)
    if \(\frac{P(x | w_1)}{P(x | w_2)} \gt \frac{P(w_2)}{P(w_1)}\) for \(\lambda_{11}=\lambda_{22}=0\) and \(\lambda_{12}=\lambda_{21}\)
    (likehood ratio \(\gt\) threshold) (위의 Bayes Decision Rule에서 구한 식과 same)
  • loss가 \(\lambda (\alpha_{i}|w_{j}) = \begin{cases} 0 & \text{if} & i = j & (\text{no penalty}) \\ 1 & \text{if} & i \neq j & (\text{equal penalty}) \end{cases}\) 일 경우
    conditional risk :
    \(R(\alpha_{i} | x) = \sum_{j=1}^c \lambda(\alpha_{i}|w_j)P(w_j|x) = \sum_{j=1, j \neq i}^c P(w_j|x) = 1 - P(w_i | x)\) 이므로
    Bayes Decision Rule에서 conditional risk \(R(\alpha_{i} | x)\) 최소화는 posterior \(P(w_i | x)\) 최대화와 같음
  • multi-class problem :
    classifieer (discriminant function) (space-partitioning function) \(g(x)\) 에 대해
    choose \(w_i\) where \(g_{i}(x)\) is the largest
    s.t. decision boundary is \(g_{i}(x) = g_{j}(x)\) where they are the two largest discriminant functions
    e.g. Bayes classifier : \(g_{i}(x) = - R(\alpha_{i} | x)\) or \(g_{i}(x) = P(w_i | x)\) or \(g_{i}(x) = P(x | w_i)P(w_i)\) or \(g_{i}(x) = \text{ln}P(x | w_i) + \text{ln}P(w_i)\)

Discriminant Function for Gaussian PDF

• \(G(\boldsymbol x) = \frac{1}{(2\pi)^{\frac{d}{2}} | \Sigma |^{\frac{1}{2}}}e^{-\frac{1}{2}(\boldsymbol x - \boldsymbol \mu)^T\Sigma^{-1}(\boldsymbol x - \boldsymbol \mu)}\)
  where \(d \times d\) covariance \(\Sigma = E[(\boldsymbol x - \boldsymbol \mu)(\boldsymbol x - \boldsymbol \mu)^T] = E[\boldsymbol x \boldsymbol x^{T}] - \boldsymbol \mu \boldsymbol \mu^{T} = S - \boldsymbol \mu \boldsymbol \mu^{T}\)
  where \(S = E[\boldsymbol x \boldsymbol x^{T}]\) : standard autocorrelation matrix

• Discriminant function for Gaussian PDF :
  likelihood \(P(x | w_i)\) 를 Gaussian PDF로 둘 경우,
  \(g_{i}(x) = \text{ln}P(x | w_i) + \text{ln}P(w_i) = -\frac{1}{2}(\boldsymbol x - \boldsymbol \mu_{i})^T\Sigma_{i}^{-1}(\boldsymbol x - \boldsymbol \mu_{i}) - \frac{d}{2} \text{ln}(2\pi) - \frac{1}{2} \text{ln} | \Sigma_{i} | + \text{ln}P(w_i)\)

  • case 1) \(\Sigma_{i} = \sigma^{2} \boldsymbol I\) (모든 classes에 대해 equal covariance) (등방성(sphere))
    \(g_{i}(x) = -\frac{\| \boldsymbol x - \boldsymbol \mu_{i} \|^2}{2 \sigma^{2}} + \text{ln}P(w_i)\)
    \(i\) 와 관련된 term만 남기면
    \(g_{i}(x) = \frac{1}{\sigma^{2}} \boldsymbol \mu_{i}^T \boldsymbol x - \frac{1}{2\sigma^{2}} \boldsymbol \mu_{i}^T \boldsymbol \mu_{i} + \text{ln}P(w_i)\)
    \(= \boldsymbol w_i^T \boldsymbol x + \boldsymbol w_{i0}\) (linear)
    • decision boundary :
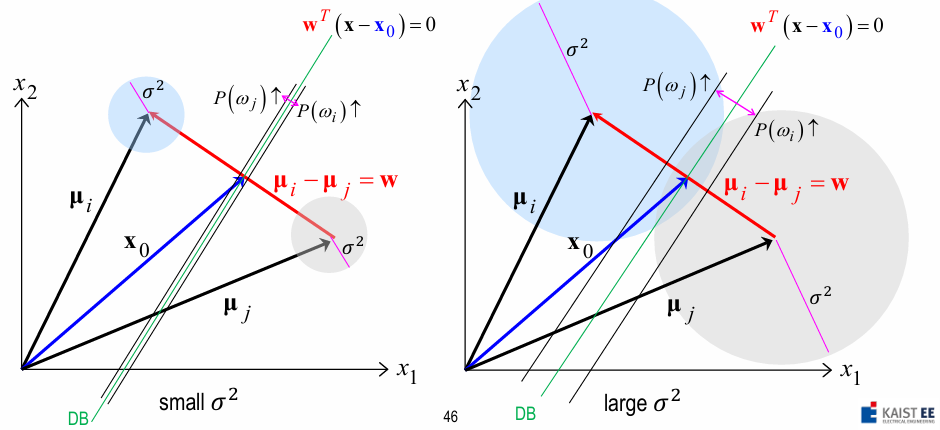
      hyperplane \(g(x) = g_{i}(x) - g_{j}(x) = (\boldsymbol \mu_{i} - \boldsymbol \mu_{j})^T(\boldsymbol x - \frac{1}{2}(\boldsymbol \mu_{i} + \boldsymbol \mu_{j}) + \frac{\sigma^{2}}{(\boldsymbol \mu_{i} - \boldsymbol \mu_{j})^T} \text{ln}\frac{P(w_i)}{P(w_j)})\)
      \(= \boldsymbol w^T (\boldsymbol x - \boldsymbol x_0) = 0\)
    • \(\boldsymbol x_0\) 를 지나고 \(\boldsymbol w = \boldsymbol \mu_{i} - \boldsymbol \mu_{j}\) 에 수직인 hyperplane
    • \(\boldsymbol x_0 = \frac{1}{2}(\boldsymbol \mu_{i} + \boldsymbol \mu_{j}) - \frac{\sigma^{2}}{\| \boldsymbol \mu_{i} - \boldsymbol \mu_{j} \|^2} \text{ln}\frac{P(w_i)}{P(w_j)} (\boldsymbol \mu_{i} - \boldsymbol \mu_{j})\) 이므로
      \(\boldsymbol x_0\) 의 위치는 \(\boldsymbol \mu_{i}\) 와 \(\boldsymbol \mu_{j}\) 의 중점에서 \(\begin{cases} \boldsymbol \mu_{j} \text{쪽으로 이동} & \text{if} & P(w_i) \gt P(w_j) \\ \boldsymbol \mu_{i} \text{쪽으로 이동} & \text{if} & P(w_i) \lt P(w_j) \end{cases}\)
      (\(P(w_i)\) 와 \(P(w_j)\) 중 더 작은 쪽으로 이동)
      (\(\sigma^{2}\) 이 (\(\| \mu_{i} - \mu_{j} \|^2\) 에 비해 비교적) 작은 경우 \(P(w_i)\) 와 \(P(w_j)\) 에 따른 \(x_0\) shift는 미약)

• Discriminant function for Gaussian PDF :
  likelihood \(P(x | w_i)\) 를 Gaussian PDF로 둘 경우,
  \(g_{i}(x) = \text{ln}P(x | w_i) + \text{ln}P(w_i) = -\frac{1}{2}(\boldsymbol x - \boldsymbol \mu_{i})^T\Sigma_{i}^{-1}(\boldsymbol x - \boldsymbol \mu_{i}) - \frac{d}{2} \text{ln}(2\pi) - \frac{1}{2} \text{ln} | \Sigma_{i} | + \text{ln}P(w_i)\)
  • case 2) \(\Sigma_{i} = \Sigma\) (symmetric) (모든 classes에 대해 equal covariance) (비등방성(hyper-ellipsoidal))
    \(g_{i}(x) = -\frac{1}{2}(\boldsymbol x - \boldsymbol \mu_{i})^T\Sigma^{-1}(\boldsymbol x - \boldsymbol \mu_{i}) + \text{ln}P(w_i)\)
    \(i\) 와 관련된 term만 남기면
    \(g_{i}(x) = \boldsymbol \mu_{i}^T \Sigma^{-1} \boldsymbol x - \frac{1}{2} \boldsymbol \mu_{i}^T \Sigma^{-1} \boldsymbol \mu_{i} + \text{ln}P(w_i)\)
    \(= \boldsymbol w_i^T \boldsymbol x + \boldsymbol w_{i0}\) (linear)
    • decision boundary :
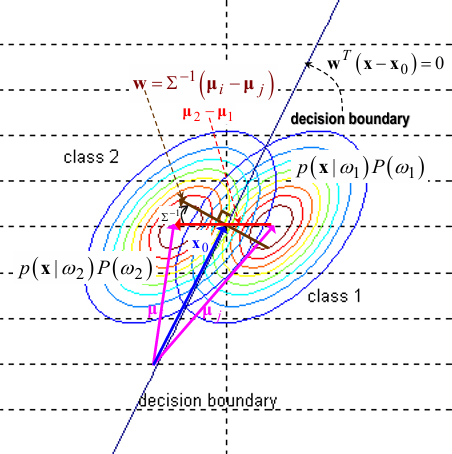
      hyperplane \(g(x) = g_{i}(x) - g_{j}(x) = (\boldsymbol \mu_{i} - \boldsymbol \mu_{j})^T \Sigma^{-1} (\boldsymbol x - \frac{1}{2}(\boldsymbol \mu_{i} + \boldsymbol \mu_{j}) + \frac{1}{(\boldsymbol \mu_{i} - \boldsymbol \mu_{j})^T \Sigma^{-1}} \text{ln}\frac{P(w_i)}{P(w_j)})\)
      \(= \boldsymbol w^T (\boldsymbol x - \boldsymbol x_0) = 0\)
    • \(\boldsymbol x_0\) 를 지나고 \(\boldsymbol w = \Sigma^{-1} (\boldsymbol \mu_{i} - \boldsymbol \mu_{j})\) 에 수직인 hyperplane
    • \(\boldsymbol x_0 = \frac{1}{2}(\boldsymbol \mu_{i} + \boldsymbol \mu_{j}) - \frac{\text{ln}\frac{P(w_i)}{P(w_j)}}{(\boldsymbol \mu_{i} - \boldsymbol \mu_{j})^T \Sigma^{-1} (\boldsymbol \mu_{i} - \boldsymbol \mu_{j})} (\boldsymbol \mu_{i} - \boldsymbol \mu_{j})\) 이므로
      마찬가지로 \(\boldsymbol x_0\) 의 위치는 \(\boldsymbol \mu_{i}\) 와 \(\boldsymbol \mu_{j}\) 의 중점에서 \(P(w_i)\) 와 \(P(w_j)\) 중 더 작은 쪽으로 이동
    • \(\boldsymbol w = \Sigma^{-1} (\boldsymbol \mu_{i} - \boldsymbol \mu_{j})\) 는
      vector \(\boldsymbol \mu_{i} - \boldsymbol \mu_{j}\) 를 \(\Sigma^{-1}\) 로 회전시킨 vector를 의미

• Discriminant function for Gaussian PDF :
  likelihood \(P(x | w_i)\) 를 Gaussian PDF로 둘 경우,
  \(g_{i}(x) = \text{ln}P(x | w_i) + \text{ln}P(w_i) = -\frac{1}{2}(\boldsymbol x - \boldsymbol \mu_{i})^T\Sigma_{i}^{-1}(\boldsymbol x - \boldsymbol \mu_{i}) - \frac{d}{2} \text{ln}(2\pi) - \frac{1}{2} \text{ln} | \Sigma_{i} | + \text{ln}P(w_i)\)
  • case 3) \(\Sigma_{i}\) is arbitrary (symmetric) (class마다 covariance 다름) (비등방성(hyper-ellipsoidal))
    \(g_{i}(x) = -\frac{1}{2}(\boldsymbol x - \boldsymbol \mu_{i})^T\Sigma_{i}^{-1}(\boldsymbol x - \boldsymbol \mu_{i}) - \frac{1}{2} \text{ln} | \Sigma_{i} | + \text{ln}P(w_i)\)
    \(\Sigma_{i}\) 가 \(i\) 에 대한 term이므로 \(- \frac{1}{2} \boldsymbol x^T \Sigma_{i}^{-1} \boldsymbol x\) term이 안 지워져서
    \(g_{i}(x) = - \frac{1}{2} \boldsymbol x^T \Sigma_{i}^{-1} \boldsymbol x + \boldsymbol \mu_{i}^T \Sigma_{i}^{-1} \boldsymbol x - \frac{1}{2} \boldsymbol \mu_{i}^T \Sigma_{i}^{-1} \boldsymbol \mu_{i} - \frac{1}{2} \text{ln} | \Sigma_{i} | + \text{ln}P(w_i)\)
    \(= - \frac{1}{2} \boldsymbol x^T \Sigma_{i}^{-1} \boldsymbol x + \boldsymbol w_i^T \boldsymbol x + \boldsymbol w_{i0}\) (quadratic) 는
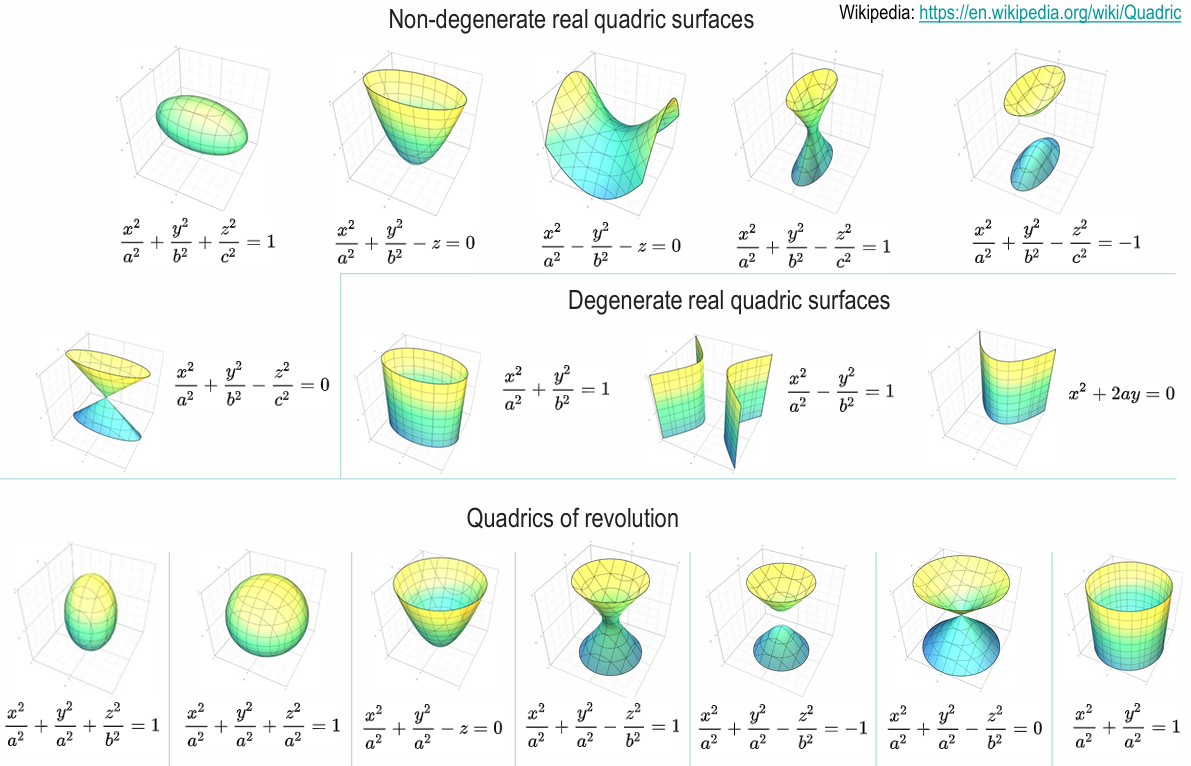
    quadratic discriminant function in \(x\)
    • decision surface :
      hyperquadratic (hyperplane, hypersphere, hyperellipsoidal, hyperparaboloid, hyperhyperboloid)

Bayes Rule for Discrete Case

• pdf 적분 $$\int p(x	w_{j}) dx$$ 대신
  확률 합 $$\text{lim}{\Delta x \rightarrow 0} \Sigma{k=-\infty}^{\infty} p(x_k	w_j) \Delta x \rightarrow \Sigma_{k=1}^m P(v_k	w_j)$$

• Bayes Decision Rule은 discrete case에서도 same
  Bayes risk minimize 위해 conditional risk \(R(\alpha_{i} | x)\) minimize
  (posterior maximize와 same)

• \(\boldsymbol x = [x_1, x_2, \ldots, x_d]^T\) 에서 \(x_i\) 가 0 혹은 1의 값을 갖는 Bernoulli random var.일 때
  • class \(w_1\) 일 때 :
    \(x_i \sim p_i^{x_i}(1-p_i)^{1-x_i}\)
    \(P(\boldsymbol x | w_1) = P([x_1, x_2, \ldots, x_d]^T | w_1) = \prod_{i=1}^d P(x_i | w_1) = \prod_{i=1}^d p_i^{x_i}(1-p_i)^{1-x_i}\)
  • class \(w_2\) 일 때 :
    \(x_i \sim q_i^{x_i}(1-q_i)^{1-x_i}\)
    \(P(\boldsymbol x | w_2) = P([x_1, x_2, \ldots, x_d]^T | w_2) = \prod_{i=1}^d P(x_i | w_2) = \prod_{i=1}^d q_i^{x_i}(1-q_i)^{1-x_i}\)
  • likelihood ratio :
    \(\frac{P(\boldsymbol x | w_1)}{P(\boldsymbol x | w_2)} = \prod_{i=1}^d (\frac{p_i}{q_i})^{x_i}(\frac{1-p_i}{1-q_i})^{1-x_i}\)
  • discriminant function :
    choose \(w_1\)
    if \(g(x) = \text{ln} \frac{P(\boldsymbol x | w_1)P(w_1)}{P(\boldsymbol x | w_2)P(w_2)} = \sum_{i=1}^d(x_i \text{ln}\frac{p_i}{q_i} + (1-x_i)\text{ln}\frac{1-p_i}{1-q_i}) + \text{ln}\frac{P(w_1)}{P(w_2)} = \sum_{i=1}^d w_ix_i + w_0 = \boldsymbol w^T \boldsymbol x + w_0 \gt 0\)
    where \(w_i = \text{ln}\frac{p_i(1-q_i)}{q_i(1-p_i)}\) and \(w_0 = \sum_{i=1}^d(\text{ln}\frac{1-p_i}{1-q_i}) + \text{ln}\frac{P(w_1)}{P(w_2)}\)
    • case 1-1) \(p_i = q_i\)
      \(w_i = 0\) , so \(x_i\) 는 class 결정에 영향 없음
    • case 1-2) \(p_i \gt q_i\)
      \(w_i \gt 0\) , so \(x_i = 1\) 은 class \(w_1\) 선택에 보탬
    • case 1-3) \(p_i \lt q_i\)
      \(w_i \lt 0\) , so \(x_i = 1\) 은 class \(w_2\) 선택에 보탬
    • case 2-1) \(P(w_1)\) 값 증가 (\(\gt P(w_2)\))
      \(w_0\) 값이 커지므로 class \(w_1\) 선택에 보탬
    • case 2-2) \(P(w_1)\) 값 감소 (\(\lt P(w_2)\))
      \(w_0\) 값이 작아지므로 class \(w_2\) 선택에 보탬

Chapter 2. Linear Transformation

Linear Transformation

• \[y = A^Tx\]
  • mean and variance :
    \(\mu_{y} = A^T \mu_{x}\)
    \(\Sigma_{y} = E[(y - \mu_{y})(y - \mu_{y})^T] = A^T \Sigma_{x} A\)
  • Mahalanobis distance :
    \(d_y^2 = (y - \mu_{y})^T\Sigma_{y}^{-1}(y - \mu_{y}) = \cdots = d_x^2\)
    linear transformation을 해도 Mahalanobis distance는 그대로임
    (Euclidean distance \((x - \mu_{x})^T(x - \mu_{x})\) 는 linear transformation을 하면 variant)
  • Gaussian distribution :
    \(x \sim N(\mu_{x}, \Sigma_{x})\) 일 때
    \(P(y) = (2 \pi)^{- \frac{d}{2}} | \Sigma_{y} |^{-\frac{1}{2}} \exp(-\frac{1}{2}(y - \mu_{y})^T \Sigma_{y}^{-1} (y - \mu_{y})) = (2 \pi)^{- \frac{d}{2}} | A |^{-1} | \Sigma_{x} |^{-\frac{1}{2}} \exp(-\frac{1}{2}(x - \mu_{x})^T \Sigma_{x}^{-1} (x - \mu_{x})) = \frac{1}{|A|} P(x)\)

Orthonormal Transformation

• \(x = \sum_{i=1}^d y_i \phi_{i}\)
  where \(\{ \phi_{i}, \cdots, \phi_{d} \}\) is orthonormal basis
  Equivalently,
  \(y_i = x^T \phi_{i}\)
  where vector \(x\) 를 i-th eigenvector \(\phi_{i}\) 에 project한 게 \(y_i\)
  • approx. \(x\) :
    • \(\{ y_{m+1}, \cdots, y_{d} \}\) 를 pre-defined constants \(\{ b_{m+1}, \cdots, b_{d} \}\) 로 대체했을 때
      \(\hat x(m) = \sum_{i=1}^m y_i \phi_{i} + \sum_{i=m+1}^d b_i \phi_{i}\)
  • optimal \(b_i\) :
    • error \(\Delta x(m) = x - \hat x(m) = \sum_{i=m+1}^d (y_i - b_i) \phi_{i}\)
      MSE \(\bar \epsilon^{2}(m) = E[| \Delta x(m) |^2] = E[\Delta x^T(m) \Delta x(m)] = \sum_{i=m+1}^d E[(y_i - b_i)^2]\)
    • orthonormal basis \(\phi_{i}, \phi_{j}\) 에 대해
      \(\frac{\partial}{\partial b_i} E[(y_i - b_i)^2] = -2(E[y_i] - b_i) = 0\) 이므로
      MSE 최소화하는 optimal \(b_i = E[y_i]\)
  • optimal \(\phi_{i}\) :
    • \(x = \sum_{j=1}^d y_j \phi_{j}\) 의 양변에 \(\phi_{i}^T\) 를 곱하면
      \(y_i = x^T \phi_{i}\) 이고
      optimal \(b_i = E[y_i]\) 이므로
      MSE \(\bar \epsilon^{2}(m) = \sum_{i=m+1}^d E[(y_i - b_i)^2] = \sum_{i=m+1}^d E[(x^T \phi_{i} - E[x^T \phi_{i}])^T(x^T \phi_{i} - E[x^T \phi_{i}])] = \sum_{i=m+1}^d \text{Var}(\phi_{i}^{T} x) = \sum_{i=m+1}^d \phi_{i}^T \Sigma_{x} \phi_{i}\)
    • orthonormality equality constraint \(\phi_{i}^T\phi_{i} = \| \phi_{i} \| = 1\) 을 만족하면서 MSE \(\bar \epsilon^{2}(m)\) 를 최소화하는 \(\phi_{i}\) 는 Lagrange multiplier Method Link 로 찾을 수 있다
      \(\rightarrow\)
      goal : minimize \(U(m) = \sum_{i=m+1}^d \phi_{i}^T \Sigma_{x} \phi_{i} + \sum_{i=m+1}^d \lambda_{i}(1 - \phi_{i}^T\phi_{i})\)
      \(\frac{\partial}{\partial x}(x^TAx) = (A + A^T)x = 2Ax\) for symmetric \(A\) 이므로
      \(\frac{\partial}{\partial \phi_{i}} U(m) = 2(\Sigma_{x}\phi_{i} - \lambda_{i}\phi_{i}) = 0\) 이므로
      MSE 최소화하는 optimal \(\phi_{i}\) 는 \(\Sigma_{x}\phi_{i} = \lambda_{i}\phi_{i}\) 을 만족하므로
      \(\phi_{i}\) 와 \(\lambda_{i}\) 는 covariance matrix \(\Sigma_{x}\) 의 eigenvector and eigenvalue 이다
• Eigenvector and Eigenvalue :
  • \(\Sigma \Phi = \Phi \Lambda\) where \(\Phi \Phi^{T} = I\)
  • If \(\Sigma\) is non-singular (\(| \Sigma | \neq 0\)),
    all eigenvalues \(\lambda\) are non-zero
  • If \(\Sigma\) is positive-definite (\(x^T \Sigma x \geq 0\) for all \(x \neq 0\)),
    all eigenvalues \(\lambda\) are positive
  • If \(\Sigma\) is real and symmetric,
    all eigenvalues \(\lambda\) are real
    and eigenvectors(w. distinct eigenvalues) are orthogonal
    • pf)
      \(\Sigma \phi_{i} = \lambda_{i} \phi_{i}\) and \(\Sigma \phi_{j} = \lambda_{j} \phi_{j}\)
      \(\phi_{j}^T \Sigma \phi_{i} - \phi_{i}^T \Sigma \phi_{j} = \phi_{j}^T \lambda_{i} \phi_{i} - \phi_{i}^T \lambda_{j} \phi_{j}\)
      \(0 = (\lambda_{i} - \lambda_{j}) \phi_{j}^T \phi_{i}\) since \(\Sigma\) is symmetric
      \(\rightarrow \phi_{j}^T \phi_{i} = 0\) (eigenvectors are orthogonal)
• Orthonormal Transformation :
  \(y = \Phi^{T} x\)
  for \(\Phi = [\phi_{1}, \cdots \phi_{d}]\) and \(\Phi \Phi^{T} = I\)
  • vector \(x\) 를 i-th eigenvector \(\phi_{i}\) 에 project한 게 \(y_{i}\)
    즉, vector \(x\) 를 new coordinate \(\Phi = [\phi_{1}, \cdots \phi_{d}]\) 으로 나타낸 게 vector \(y\)
  • eigenvector는 principal axis를 나타내고, eigenvalue는 해당 방향으로 퍼진 정도를 나타냄
  • \(y\) 의 covariance matrix인 \(\Sigma_{y}\) 는 diagonal matrix
    (uncorrelated random vector \(y\))
    • \(\Sigma_{y}\)
      \(= \Phi^{T} \Sigma_{x} \Phi\)
      \(= \Phi^{T} \Phi \Lambda\) since \(\Sigma \Phi = \Phi \Lambda\)
      \(= \Phi^{-1} \Phi \Lambda\) since eigenvector matrix is orthogonal matrix (\(\Phi^{T} = \Phi^{-1}\))
      \(= \Lambda\)
  • distance :
    • Mahalanobis distance는 any linear transformation에 대해 보존됨
    • Euclidean distance는 linear transformation 중 orthonormal transformation일 때만 보존됨
      \(\| y \|^2 = y^Ty = x^T \Phi \Phi^{T} x = x^T \Phi \Phi^{-1} x = x^T x = \| x \|^2\)

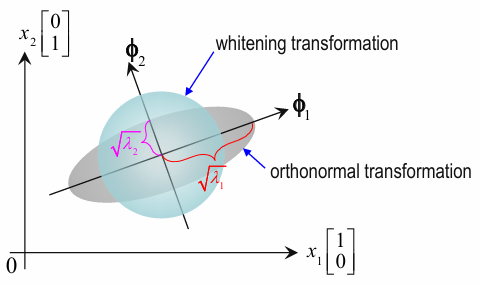
Whitening Transformation

• Whitening Transformation :
  \(y = \Lambda^{-\frac{1}{2}} \Phi^{T} x = (\Phi \Lambda^{-\frac{1}{2}})^T x\)
  (Orthonormal Transformation을 한 뒤 추가로 \(\Lambda^{-\frac{1}{2}}\) 로 transformation)
  • \(y\) 의 covariance matrix인 \(\Sigma_{y}\) 는 identity matrix \(I\)
    • \(\Sigma_{y}\)
      \(= (\Lambda^{-\frac{1}{2}} \Phi^{T}) \Sigma_{x} (\Phi \Lambda^{-\frac{1}{2}})\)
      \(= \Lambda^{-\frac{1}{2}} \Lambda \Lambda^{-\frac{1}{2}}\)
      \(= I\)
  • \(\Lambda^{-\frac{1}{2}}\) 은 principal components의 scale을 \(\frac{1}{\sqrt{\lambda_{i}}}\) 배 하는 효과
  • Whitening Transformation을 한 번 하고나면,
    그 후에 any Orthonormal Transformation(\(y = \Phi^{T} x\) for \(\Psi \Psi^{T} = I\))을 해도
    covariance matrix는 항상 \(\Psi I \Psi^{T} = I\)

Sample Separation

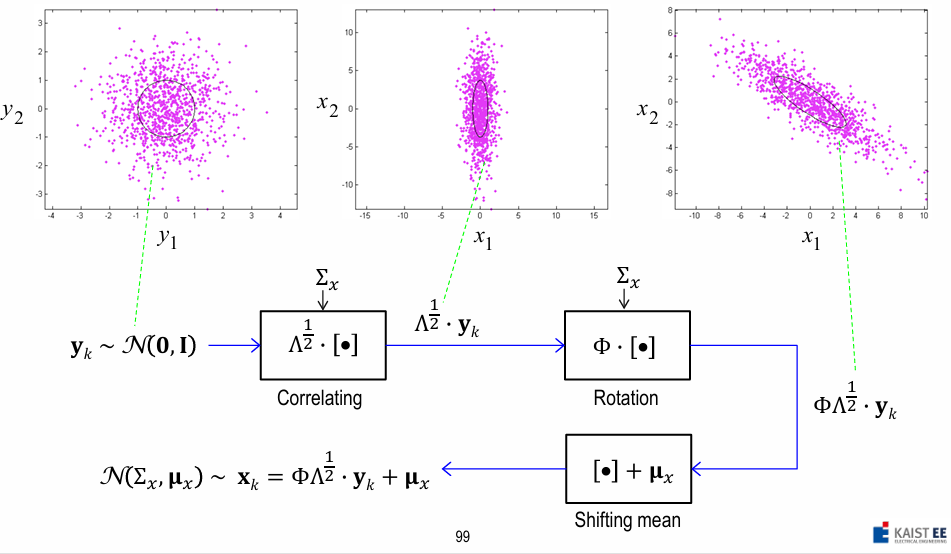
• Sample Separation :
  uncorrelated normal samples \(\sim N(0, I)\) 로부터 correlated sample \(\sim N(\mu_{x}, \Sigma_{x})\) 만들기
  • How? :
    given data \(x\) 에서 \(\mu_{x}\) 를 뺀 뒤 Whitening Transformation 적용하면 \(N(0, I)\) 이므로 이 과정을 역으로 실행
  • Step 1) Normal distribution으로부터 N개의 \(d\) -dim. independent vectors를 sampling
    \(y_1, y_2, \cdots, y_N \sim N(0, I)\)
  • Step 2) Inverse-Whitening-Transformation 적용하여 Normal distribution을 x-space로 변환 \(x_k = \Phi \Lambda^{\frac{1}{2}} y_k\)
    for given \(\Sigma_{x}\)
    and its eigen-decomposition \(\Sigma_{x} \Phi = \Phi \Lambda\)
  • Step 3) x-space의 samples에 \(\mu_{x}\) 더함
    \(x_k = \Phi \Lambda^{\frac{1}{2}} y_k + \mu_{x} \sim N(\mu_{x}, \Sigma_{x})\)
    for given \(\mu_{x}\)

Chapter 3. Maximum-likelihood and Bayesian Parameter Estimation

• parameter estimation :
  • Maximum Likelihood Estimation (MLE) :
    (true) parameters are unknown, but fixed
    estimators are random variable
  • Bayesian Estimation :
    parameters are random variables and prior is known

Maximum Likelihood Estimation (MLE)

• Assumption :
  training data \(D_j\) \(\sim\) likelihood \(p(D_j | w_j) = N(\mu_{j}, \Sigma_{j})\)
  (i.i.d random samples)

• MLE :
  • likelihood :
    \(\hat \theta = \text{argmax}_{\theta} p(D=\{ x_1, x_2, \ldots, x_n \} | \theta) = \text{argmax}_{\theta} \prod_{k=1}^n p(x_k | \theta)\)
  • log-likelihood :
    \(\hat \theta = \text{argmax}_{\theta} p(D=\{ x_1, x_2, \ldots, x_n \} | \theta) = \text{argmax}_{\theta} \sum_{k=1}^n \text{ln} p(x_k | \theta)\)
• Gaussian likelihood :
  • unknown \(\mu\) :
    • likelihood :
      \(p(x_k | \mu) = (2 \pi)^{-\frac{d}{2}} | \Sigma |^{-\frac{1}{2}} \text{exp}(-\frac{1}{2}(x_k - \mu)^T \Sigma^{-1} (x_k - \mu))\)
      \(p(D=\{ x_1, x_2, \ldots, x_N \} | \mu) = \prod_{k=1}^N p(x_k | \mu) = (2 \pi)^{-\frac{dN}{2}} | \Sigma |^{-\frac{N}{2}} \text{exp}(-\frac{1}{2} \sum_{k=1}^N (x_k - \mu)^T \Sigma^{-1} (x_k - \mu))\)
    • log-likelihood :
      \(\text{ln} p(D | \mu) = -\frac{dN}{2} \text{ln}(2 \pi) -\frac{N}{2} \text{ln} | \Sigma | -\frac{1}{2} \sum_{k=1}^N (x_k - \mu)^T \Sigma^{-1} (x_k - \mu)\)
    • matrix derivative :
      \(\frac{d}{dx}(Ax) = A\)
      \(\frac{d}{dx}(y^TAx) = A^Ty\)
      \(\frac{d}{dx}(x^TAx) = (A+A^T)x\)
      \(\frac{d}{dA}(x^TAx) = xx^T\)
      \(\frac{\partial |A|}{\partial A} = (\text{adj}(A))^T = |A|(A^{-1})^T\)
      \(\frac{\partial \text{ln}|A|}{\partial A} = (A^{-1})^T = (A^T)^{-1}\) where \(|A| = \frac{1}{|A^{-1}|}\)
    • MLE problem :
      \(\nabla_{\mu} \text{ln} p(D | \mu) = -\frac{1}{2} \sum_{k=1}^N ((\Sigma^{-1} + (\Sigma^{-1})^T) (x_k - \mu)) \times (-1) = (\Sigma^{-1} + (\Sigma^{-1})^T)(\sum_{k=1}^N x_k - \sum_{k=1}^N \mu) = 0\)
      \(\sum_{k=1}^N x_k - N \mu = 0\)
      \(\hat \mu_{\text{MLE}} = \frac{1}{N} \sum_{k=1}^N x_k\)
    • Summary :
      • \(\hat \mu_{\text{MLE}} = \frac{1}{N} \sum_{k=1}^N x_k\)
        (true mean의 MLE estimator는 sample mean)
      • \(E[\hat \mu_{\text{MLE}}] = \mu\)
        (\(\hat \mu_{\text{MLE}}\) 는 unbiased estimator)
  • unknown \(\mu\) and \(\Sigma\) :
    • log-likelihood :
      \(\text{ln} p(D | \mu) = -\frac{dN}{2} \text{ln}(2 \pi) -\frac{N}{2} \text{ln} | \Sigma | -\frac{1}{2} \sum_{k=1}^N (x_k - \mu)^T \Sigma^{-1} (x_k - \mu) = -\frac{dN}{2} \text{ln}(2 \pi) + \frac{N}{2} \text{ln} | \Sigma^{-1} | -\frac{1}{2} \sum_{k=1}^N (x_k - \mu)^T \Sigma^{-1} (x_k - \mu)\)
    • MLE problem :
      \(\nabla_{\Sigma^{-1}} \text{ln} p(D | \mu) = \frac{N}{2}\Sigma^{T} - \frac{1}{2} \sum_{k=1}^N (x_k - \mu)(x_k - \mu)^T = 0\)
      \(N \Sigma^{T} = \sum_{k=1}^N (x_k - \mu)(x_k - \mu)^T\)
      \(\mu = \hat \mu_{\text{MLE}}\) 대입하고, \(\Sigma\) 는 symmetric(\(\Sigma^{T} = \Sigma\))하므로
      \(\hat \Sigma_{\text{MLE}} = \frac{1}{N} \sum_{k=1}^N (x_k - \hat \mu_{\text{MLE}})(x_k - \hat \mu_{\text{MLE}})^T\)
    • Summary :
      • \(\hat \Sigma_{\text{MLE}} = \frac{1}{N} \sum_{k=1}^N (x_k - \hat \mu_{\text{MLE}})(x_k - \hat \mu_{\text{MLE}})^T\)
        (\(\mu\) 먼저 estimate한 뒤 \(\Sigma\) estimate)
      • \(E[\hat \Sigma_{\text{MLE}}] = \frac{1}{N} E[\sum_{k=1}^N (x_k - \hat \mu_{\text{MLE}})(x_k - \hat \mu_{\text{MLE}})^T] = \frac{N-1}{N} \Sigma \neq \Sigma\)
        (\(\hat \Sigma_{\text{MLE}}\) 는 biased estimator)
        • pf) 아래 식 이용
          \(E[x_i x_j^T] = \begin{cases} \Sigma + \mu \mu^{T} & \text{if} & i = j \\ \mu \mu^{T} & \text{if} & i \neq j \end{cases}\)
          since \(\Sigma = E[(x - \mu)(x - \mu)^T] = \cdots = E[xx^T] - \mu \mu^{T}\)
          since \(0 = E[(x_i - \mu)(x_j - \mu)^T] = E[x_i x_j^T] - \mu \mu^{T}\) by independence \(i \neq j\)
      • \(\text{lim}_{N \rightarrow \infty}E[\hat \Sigma_{\text{MLE}}] = \text{lim}_{N \rightarrow \infty} \frac{N-1}{N} \Sigma = \Sigma\)
        (\(\hat \Sigma_{\text{MLE}}\) 는 asymptotically unbiased estimator)
        또는
        \(\hat \Sigma_{\text{MLE}} = \frac{1}{N-1} \sum_{k=1}^N (x_k - \hat \mu_{\text{MLE}})(x_k - \hat \mu_{\text{MLE}})^T\)
        (위처럼 설정하면 \(\hat \Sigma_{\text{MLE}}\) 는 unbiased estimator)
• MLE :
  • MLE is asymptotically consistent
    if \(\text{lim}_{N \rightarrow \infty} P(\| \hat \theta_{\text{MLE}} - \theta_{\text{true}} \| \leq \epsilon) = 1\) for arbitrary small \(\epsilon\)
    (sample 수 \(N\) 이 크면 param. estimate은 true value랑 거의 비슷)
    by central limit theorem and the fact that MLE is related to the sum of random var.
  • MLE is asymptotically efficient
    since MLE는 Cramer-Rao lower bound(any estimate이 달성할 수 있는 the lowest value of variance)

Bayesian Estimation

• Summary :
  • MLE (maximum likelihood estimation) :
    • \(\theta\) is unknown, but fixed

    • maximize likelihood $$\theta_{MLE} = \text{argmax}_{\theta} p(D

      \theta)$$

  • MAP (maximum a posterior) :
    • \(\theta\) is random var. and prior \(p(\theta)\) is known

    • maximize posterior $$\theta_{MAP} = \text{argmax}_{\theta} p(\theta

      D) = \text{argmax}_{\theta} \text{ln} p(D

      \theta) + \text{ln} p(\theta)$$

  • If prior \(p(\theta)\) is constant (uniform distribution),
    MLE와 MAP는 same

• prior \(p(\theta)\) 와 posterior \(p(\theta | D)\) 가 같은 확률 분포의 형태를 가질 경우
  prior \(p(\theta)\) 를
  likehood \(p(D | \theta)\) 에 대한 conjugate prior라고 말한다

• Gaussian case :
  • random var. \(\mu\) :
    • likelihood and conjugate prior :
      \(x_k \sim\) \(p(x_k | \mu) = N(\mu, \sigma^{2})\)
      where \(\mu \sim\) \(p(\mu) = N(\mu_{0}, \sigma_{0}^{2})\)
    • posterior (수식 유도는 아래에 별도로) :
      \(p(\mu | D, \sigma^{2}) \propto N(\mu_{N}, \sigma_{N}^{2})\)
      \(= \frac{1}{\sqrt{2 \pi} \sigma_{N}} e^{-\frac{1}{2}(\frac{\mu - \mu_{N}}{\sigma_{N}})^2}\)
      where \(\hat \mu_{MAP} = \text{argmax}_{\mu} p(\mu | D, \sigma^{2}) = \mu_{N} = (\frac{N}{N + \frac{\sigma^{2}}{\sigma_{0}^{2}}}) \hat \mu_{MLE} + \frac{\frac{\sigma^{2}}{\sigma_{0}^{2}}}{N + \frac{\sigma^{2}}{\sigma_{0}^{2}}} \mu_{0}\)
      where \(\sigma_{N}^{2} = \frac{\sigma^{2}}{N + \frac{\sigma^{2}}{\sigma_{0}^{2}}}\)
      • Bayesian Learning :
        \(N\), 즉 sample 수가 많아질수록
        \(\mu_{N}\) 은 \(\hat \mu_{MLE}\) 에 가까워지고
        \(\sigma_{N}^{2}\), 즉 uncertainty about \(\mu_{N}\) 은 감소
        따라서 \(N \rightarrow \infty\) 이면
        posterior \(p(\mu | D, \sigma^{2})\) 는 \(\mu_{N} = \hat \mu_{MLE}\) 에서의 Dirac delta function
      • \(\hat \mu_{MAP} = \mu_{N}\) 에서
        \((\frac{N}{N + \frac{\sigma^{2}}{\sigma_{0}^{2}}}) \hat \mu_{MLE}\) 는 empirical data samples 부분이고
        \(\frac{\frac{\sigma^{2}}{\sigma_{0}^{2}}}{N + \frac{\sigma^{2}}{\sigma_{0}^{2}}} \mu_{0}\) 는 prior info. 부분
      • 만약 \(\sigma_{0}^{2} = 0\) 이라면
        prior : variance \(\sigma_{0}^{2}\) 가 매우 작으므로, certain that \(\mu = \mu_{0}\)
        So,
        posterior : \(\mu_{N} = \mu_{0}\) (data samples는 \(\mu_{N}\) 에 영향 없음)
      • 만약 \(\sigma^{2} \ll \sigma_{0}^{2}\) 이라면
        prior : variance \(\sigma_{0}^{2}\) 가 매우 크므로, so uncertain that \(\mu = \mu_{0}\)
        So,
        posterior : \(\mu_{N} = \hat \mu_{MLE}\) (data samples가 \(\mu_{N}\) 에 대부분의 영향 미침)
    • posterior (수식 유도) :
      \(p(\mu | D, \sigma^{2})\)
      \(\propto p(D | \mu, \sigma^{2}) p(\mu) = \frac{1}{(2 \pi \sigma^{2})^{\frac{N}{2}}(2 \pi \sigma_{0}^{2})^{\frac{1}{2}}}e^{-\frac{1}{2\sigma^{2}}\sum_{i=1}^N(x_i - \mu)^2 -\frac{1}{2\sigma_{0}^{2}}(\mu - \mu_{0})^2}\)
      \(\propto e^{-\frac{1}{2\sigma^{2}}\sum_{i=1}^N(x_i - \mu)^2 -\frac{1}{2\sigma_{0}^{2}}(\mu - \mu_{0})^2}\)
      \(\propto e^{-\frac{1}{2\sigma^{2}}(N \mu^{2} - 2 \mu \sum_{i=1}^N x_i) -\frac{1}{2\sigma_{0}^{2}}(\mu^{2} - 2 \mu \mu_{0})}\)
      \(= e^{-\frac{1}{2}(\mu^{2}(\frac{N}{\sigma^{2}} + \frac{1}{\sigma_{0}^{2}}) - 2 \mu (\frac{N \hat \mu_{MLE}}{\sigma^{2}} + \frac{\mu_{0}}{\sigma_{0}^{2}}))}\)
      \(\propto \frac{1}{\sqrt{2 \pi} \sigma_{N}} e^{-\frac{1}{2}(\frac{\mu - \mu_{N}}{\sigma_{N}})^2}\)
      where \(\hat \mu_{MAP} = \mu_{N} = (\frac{N\sigma_{0}^{2}}{N\sigma_{0}^{2} + \sigma^{2}}) \hat \mu_{MLE} + \frac{\sigma^{2}}{N\sigma_{0}^{2} + \sigma^{2}} \mu_{0}\)
      where \(\sigma_{N}^{2} = \frac{\sigma_{0}^{2} \sigma^{2}}{N\sigma_{0}^{2} + \sigma^{2}}\)

Principal Component Analysis (PCA)

• PCA :
  “curse of dimensionality” 문제 완화하고자
  dimensionality reduction w/o losing much info.
  • Step 1)
    각 dim.에서의 mean을 빼서 zero-mean data로 만듦
  • Step 2)
    variance \(E_{x}[(u^T x)^2]\) 를 최대화하는 direction \(u\) 가 first principal component
    (\(u^T x\) : vector \(x\) 를 unit vector \(u\) 에 projection한 것)
    • Step 2-1)
      \(E_{x}[(u^T x)^2] = E_{x}[(u^T x)(u^T x)^T] = u^T E_{x}[xx^T] u = u^T C u\)
      where \(C = E_{x}[xx^T]\) (or \(\hat C = \frac{1}{N-1} xx^T\)) : covariance matrix of \(x\) w. zero-mean
    • Step 2-2)
      \(u = \text{argmax}_{u} E_{x}[(u^T x)^2] = \text{argmax}_{u} u^T C u\) subject to \(\| u \| = | u^T u | = 1\)
      By Lagrange mutliplier Method Link,
      \(u = \text{argmax}_{u} (u^T C u - \lambda (u^T u - 1))\)
      \(\rightarrow\)
      \(\frac{d}{du}(u^T C u - \lambda (u^T u - 1)) = 2(Cu - \lambda u) = 0\)
      \(\rightarrow\)
      \(C u = \lambda u\)
      where \(u\) is eigenvector of \(C = E_{x}[xx^T]\) (or \(\hat C = \frac{1}{N-1} xx^T\)) with eigenvalue \(\lambda\)
  • Step 3)
    정리하면
    • Step 3-0) \(C\) :
      \(C = E_{x}[xx^T]\) (or \(\hat C = \frac{1}{N-1} xx^T\))는
      covariance matrix of \(x\) w. zero-mean
    • Step 3-1) \(u\) :
      principal component \(u\) 는 \(C\) 의 eigenvector
    • Step 3-2) \(\lambda\) :
      \(\lambda\) 는 \(C\) 의 eigenvalue 이자,
      direction \(u\) 에 대한 variance (\(\text{max}_{u} u^T C u = \lambda\))
  • Step 4)
    \(x = a_1 u_1 + \cdots + a_d u_d \approx \sum_{k=1}^{d^{'} \lt d} a_k u_k\)
    (any vector \(x\) in original space는
    linear comb. of eigenvectors로 표현할 수 있는데,
    덜 중요한 eigenvector 쳐내서 (dim. reduction) 근사 가능)

Multiple Discriminant Analysis (MDA)

• Dimensionality reduction :
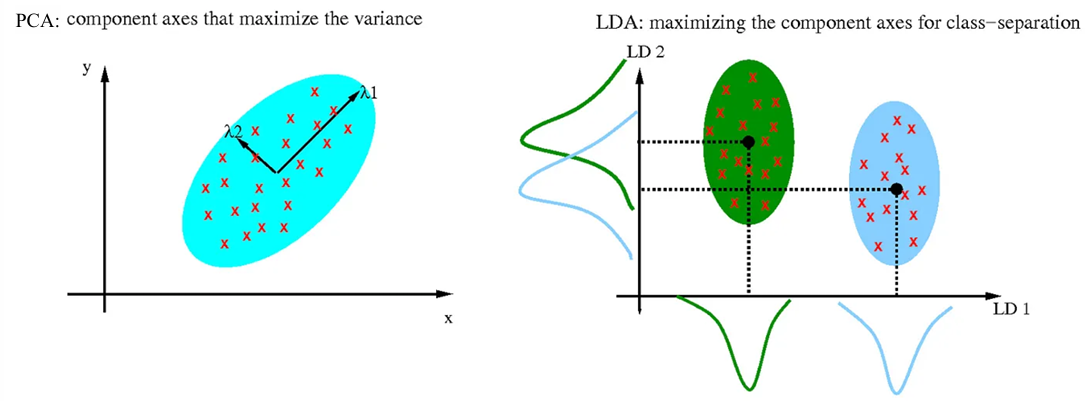
  • PCA :
    data를 가장 잘 represent하는 projection 찾기
    maximize variance
    representative
    unsupervised learning
  • MDA :
    data를 가장 잘 separate하는 projection 찾기
    maximize between-variance and minimize within-variance
    discriminative
    supervised learning

• Fisher’s LDA (Linear Discriminant Analysis) :
  • goal :
    Project onto 1D line 할 때
    \(y_k = \boldsymbol w^T \boldsymbol x_k\) where \(\| \boldsymbol \| = 1\)
    • maximize separation b.w. means of projected classes
    • minimize variance within each projected class
  • Step 1-1)
    To maximize between-class separation and minimize within-class variance,
    maximize \(J(\boldsymbol w) = \frac{(\mu_{1} - \mu_{2})^2}{\sigma_{1}^2 + \sigma_{2}^2} = \frac{(\boldsymbol w^T \boldsymbol \mu_{1} - \boldsymbol w^T \boldsymbol \mu_{2})^2}{\boldsymbol w^T (\Sigma_{1} + \Sigma_{2}) \boldsymbol w}\)
    where exact mean \(\mu_{i} = E_{\boldsymbol x}[y_i] = E_{\boldsymbol x}[\boldsymbol w^T \boldsymbol x_i] = \int \boldsymbol w^T \boldsymbol x_i p(\boldsymbol x_i) d \boldsymbol x_i = \boldsymbol w^T \int \boldsymbol x_i p(\boldsymbol x_i) d \boldsymbol x_i = \boldsymbol w^T \boldsymbol \mu_{i}\)
    where exact variance \(\sigma_{i}^2 = E_{\boldsymbol x}[(y_i - \mu_{i})^2] = \int (y_i - \mu_{i})^2 p(\boldsymbol x_i) d \boldsymbol x_i = \int (\boldsymbol w^T \boldsymbol x_i - \boldsymbol w^T \boldsymbol \mu_{i})^2 p(\boldsymbol x_i) d \boldsymbol x_i = \boldsymbol w^T \int (\boldsymbol x_i - \boldsymbol \mu_{i}) (\boldsymbol x_i - \boldsymbol \mu_{i})^{T} p(\boldsymbol x_i) d \boldsymbol x_i \boldsymbol w = \boldsymbol w^T \Sigma_{i} \boldsymbol w\)
  • Step 1-2)
    Find optimal \(w\)
    • \[\frac{\partial J}{\partial \boldsymbol w} = \frac{\partial J}{\partial \mu_{1}} \frac{\partial \mu_{1}}{\partial \boldsymbol w} + \frac{\partial J}{\partial \mu_{2}} \frac{\partial \mu_{2}}{\partial \boldsymbol w} + \frac{\partial J}{\partial \sigma_{1}^2} \frac{\partial \sigma_{1}^2}{\partial \boldsymbol w} + \frac{\partial J}{\partial \sigma_{2}^2} \frac{\partial \sigma_{2}^2}{\partial \boldsymbol w} = 0\]
      • \[\frac{\partial J}{\partial \mu_{1}} \frac{\partial \mu_{1}}{\partial \boldsymbol w} = \frac{2(\mu_{1} - \mu_{2})}{\sigma_{1}^2 + \sigma_{2}^2} \boldsymbol \mu_{1}\]
      • \[\frac{\partial J}{\partial \mu_{2}} \frac{\partial \mu_{2}}{\partial \boldsymbol w} = - \frac{2(\mu_{1} - \mu_{2})}{\sigma_{1}^2 + \sigma_{2}^2} \boldsymbol \mu_{2}\]
      • \[\frac{\partial J}{\partial \sigma_{1}^2} \frac{\partial \sigma_{1}^2}{\partial \boldsymbol w} = - \frac{(\mu_{1} - \mu_{2})^2}{(\sigma_{1}^2 + \sigma_{2}^2)^2} (\Sigma_{1} + \Sigma_{1}^{T}) \boldsymbol w\]
      • \[\frac{\partial J}{\partial \sigma_{2}^2} \frac{\partial \sigma_{2}^2}{\partial \boldsymbol w} = - \frac{(\mu_{1} - \mu_{2})^2}{(\sigma_{1}^2 + \sigma_{2}^2)^2} (\Sigma_{2} + \Sigma_{2}^{T}) \boldsymbol w\]
    • \[\frac{\partial J}{\partial \boldsymbol w} = \frac{2(\mu_{1} - \mu_{2})}{\sigma_{1}^2 + \sigma_{2}^2}(\boldsymbol \mu_{1} - \boldsymbol \mu_{2}) - \frac{2(\mu_{1} - \mu_{2})^2}{(\sigma_{1}^2 + \sigma_{2}^2)^2} (\Sigma_{1} + \Sigma_{2}) \boldsymbol w = 0\]
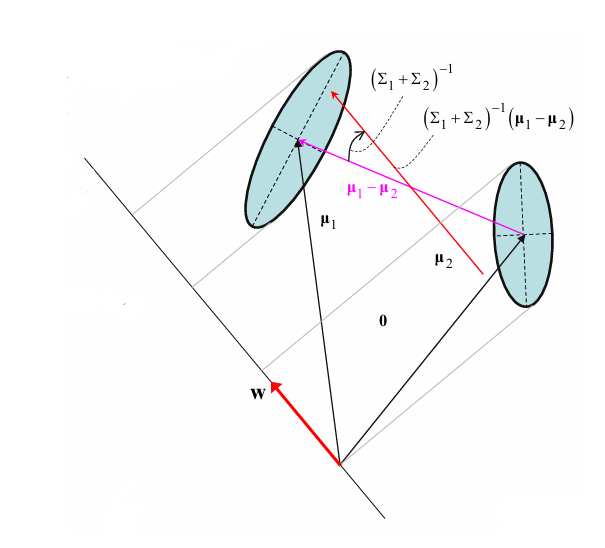
    • optimal \(\boldsymbol w = \frac{\sigma_{1}^2 + \sigma_{2}^2}{\mu_{1} - \mu_{2}}(\Sigma_{1} + \Sigma_{2})^{-1}(\boldsymbol \mu_{1} - \boldsymbol \mu_{2})\)
      where \(\boldsymbol w\) 의 방향은 \(\boldsymbol \mu_{1} - \boldsymbol \mu_{2}\) 를 \((\Sigma_{1} + \Sigma_{2})^{-1}\) 만큼 rotate시킨 방향
    • 근데, exact mean \(\mu_{i}\) and variance \(\sigma_{i}\) are unknown!
      \(\rightarrow\) 아래의 방식으로 해결
  • Step 2-1)
    Another form of \(J(\boldsymbol w)\)
    maximize \(J(\boldsymbol w) = \frac{\boldsymbol w^{T} S_{B} \boldsymbol w}{\boldsymbol w^{T} S_{w} \boldsymbol w} = \frac{\text{among group variance}}{\text{within group variance}}\)
    • within-class scatter matrix \(S_w = S_1 + S_2\) : \(d \times d\) matrix with rank \(d\)
      where scatter matrix \(S_i = \sum_{\boldsymbol x \in D_i} (\boldsymbol x - \boldsymbol m_i) (\boldsymbol x - \boldsymbol m_i)^{T}\)
      where sample mean \(\boldsymbol m_i = \frac{1}{n_i} \sum_{\boldsymbol x \in D_i} \boldsymbol x\)
    • between-class scatter matrix \(S_B = (\boldsymbol m_1 - \boldsymbol m_2) (\boldsymbol m_1 - \boldsymbol m_2)^{T}\) : \(d \times d\) matrix with rank \(1\)
  • Step 2-2)
    Find optimal \(w\)
    • \[\frac{\partial J}{\partial \boldsymbol w} = 0\]
      • \[(S_B + S_{B}^{T}) \boldsymbol w (\boldsymbol w^{T} S_{w} \boldsymbol w) - (\boldsymbol w^{T} S_{B} \boldsymbol w) (S_w + S_{w}^{T}) \boldsymbol w = 0\]
    • Since \(S_B\) and \(S_w\) are symmetric and positive-definite,
      \(S_{w}^{-1} S_B \boldsymbol w = \lambda \boldsymbol w\)
      where \(\lambda = (\boldsymbol w^{T} S_{B} \boldsymbol w) (\boldsymbol w^{T} S_{w} \boldsymbol w)^{-1} = J(\boldsymbol w)\)
      • \(\text{rank}(S_{w}^{-1} S_B) = \text{rank}(S_B) = 1\) 이므로 \(\lambda = \lambda_{1} \gt \lambda_{2} = \cdots = \lambda_{d} = 0\)
        즉, \(\lambda\) 는 only nonzero eigenvalue of \(S_{w}^{-1} S_B\)
        그리고 \(\boldsymbol w\) 는 \(\lambda\) 에 대응되는 eigenvector

• Summary on Fisher’s LDA (Linear Discriminant Analysis) :
  • slowest way :
    • inverse matrix \(S_{w}^{-1}\) 구함
    • matrix multiplication \(S_{w}^{-1}S_B\) 수행
    • \(S_{w}^{-1}S_B\) 의 nonzero eigenvalue \(\lambda\) 에 대응되는 eigenvector \(\boldsymbol w\) 구하기
  • better way :
    • MATLAB eigs(A, B) 함수로 generalized eigenvalue problem \(S_{B} \boldsymbol w = \lambda S_{w} \boldsymbol w\) 풀기
  • smartest way :
    • \(\lambda \boldsymbol w = S_{w}^{-1} S_{B} \boldsymbol w = S_{w}^{-1} (\boldsymbol m_{1} - \boldsymbol m_{2}) (\boldsymbol m_{1} - \boldsymbol m_{2})^{T} \boldsymbol w = S_{w}^{-1} (\boldsymbol m_{1} - \boldsymbol m_{2}) k \propto S_{w}^{-1} (\boldsymbol m_{1} - \boldsymbol m_{2})\)
      for constant \(k = (\boldsymbol m_{1} - \boldsymbol m_{2})^{T} \boldsymbol w = (\text{1 x d})(\text{d x 1}) = \text{1 x 1}\)
    • 즉,
      optimal \(\boldsymbol w = q S_{w}^{-1} (\boldsymbol m_{1} - \boldsymbol m_{2})\)
      for constant \(q = \frac{1}{\sqrt{(\boldsymbol m_{1} - \boldsymbol m_{2})^{T} S_{w}^{-2} (\boldsymbol m_{1} - \boldsymbol m_{2})}}\) s.t. \(\boldsymbol w^{T} \boldsymbol w = 1\)
    • \(\boldsymbol w\) 의 방향은 \(\boldsymbol \mu_{1} - \boldsymbol \mu_{2}\) 를 \(S_{w}^{-1}\) 만큼 rotate시킨 방향
• trade-off :
  • high-dim. :
    high performance (low error rate), but high computational complexity
  • low-dim. :
    low performance (high error rate), but low computational complexity
• Multiple Discriminant Analysis (MDA) :
  • goal :
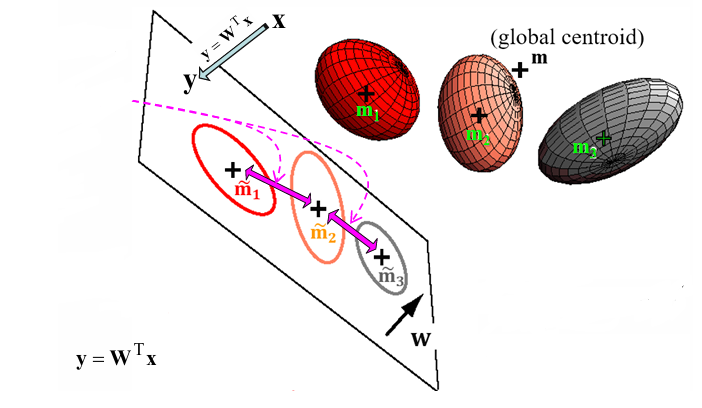
    \(c\)-class의 경우 \(c-1\) 개의 discriminant function으로 \(c-1\) 개의 1D projection 수행
    즉, Project onto \(c-1\) dim. : \(\boldsymbol y = W^{T} \boldsymbol x = [y_1, y_2, \cdots, y_{c-1}]\) by projection matrix \(W = [w_1 | w_2 | \cdots | w_{c-1}]\)
  • Fisher’s LDA에서와 유사하게
    • within-class scatter matrix : \(S_w = \sum_{i=1}^c S_i\) : \(d \times d\) matrix with rank \(d\)
      where \(S_i = \sum_{\boldsymbol x \in D_i} (\boldsymbol x - \boldsymbol m_i) (\boldsymbol x - \boldsymbol m_i)^{T}\) : scatter matrix of each class
      where \(\boldsymbol m_{i} = \frac{1}{n_i} \sum_{\boldsymbol x \in D_i} \boldsymbol x\) : sample mean of each class in \(d\)-dim.
    • between-class scatter matrix : \(S_B = \sum_{i=1}^c n_i (\boldsymbol m_i - \boldsymbol m) (\boldsymbol m_i - \boldsymbol m)^{T}\) : \(d \times d\) matrix with rank \(\leq c-1\)
      where \(n_i\) : weight for unbalanced data
      where \(\boldsymbol m = \frac{1}{n} \sum \boldsymbol x = \frac{1}{n} \sum_{j=1}^c n_j \boldsymbol m_j\) : global mean in \(d\)-dim.
    • projected within-class scatter matrix : \(\tilde S_w = \cdots = W^{T} S_w W\)
    • projected between-class scatter matrix : \(\tilde S_B = \cdots = W^{T} S_B W\)
  • \[\text{max}_{\| W \| = 1} \frac{| \tilde S_B |}{| \tilde S_w |} = \text{max}_{\| W \| = 1} \frac{| W^{T} S_B W |}{| W^{T} S_w W |} = \text{max}_{\| W \| = 1} \frac{\text{among group variance}}{\text{within group variance}}\]
  • Fisher’s LDA에서와 유사한 과정으로 풀면
    \(S_{w}^{-1} S_{B} W = \Gamma W\)
    for \(\Gamma = \begin{bmatrix} \lambda_{1} & \cdots & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \lambda_{c-1} \end{bmatrix}\)
    for \(\text{rank}(S_{w}^{-1} S_{B}) = \text{rank}(S_B) \leq c-1\)

• Limitation of LDA and MDA :
  • dim. reduction only to \(c-1\) dim. (unlike PCA)
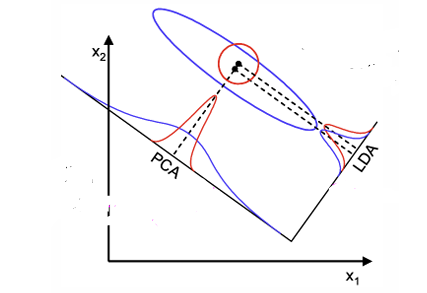
  • unimodal Gaussian likelihoods를 가정하는 parametric method라서
    만약 실제 distribution이 Gaussian 분포와 멀다면
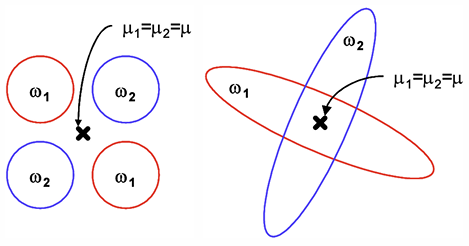
    MDA projection은 기존 분포의 복잡한 구조를 잘 보존하지 못함
  • LDA, MDA는 mean difference에 의존하여 discriminate하기 때문에
    \(\mu_{1} = \mu_{2}\) 라면 \(J(\boldsymbol w) = 0\) 이라서 LDA, MDA 적용 불가능

mean difference가 크지 않으면 LDA보다 PCA가 class separation 유리한 상황도 있음

Singular Value Decomposition (SVD)

• 쓰임 : matrix factorization
  • low-rank approximation of matrix
  • pseudo-inverse of non-square matrix
• Singular Value Decomposition (SVD) :
  \(A = U \Sigma V^T = \begin{bmatrix} u_1 & u_2 & \cdots & u_m \end{bmatrix} \begin{bmatrix} \sigma_{1} & \cdots & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \sigma_{r} & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \cdots & \sigma_{m} & 0 & \cdots & 0 \end{bmatrix} \begin{bmatrix} v_1^{T} \\ v_2^{T} \\ \vdots \\ v_n^{T} \end{bmatrix}\)
  where \(U\) is \(m \times m\) orthonormal matrix (\(UU^T = I\))
  where \(V\) is \(n \times n\) orthonormal matrix (\(VV^T = I\))
  where \(\Sigma\) is \(m \times n\) diagonal matrix (\(\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{m} \geq 0\))
  • \(AA^T = U \Sigma \Sigma^{T} U^T\)
    \(U\) 는 \(AA^T\) 의 eigenvector matrix
    \(\sigma_{i} = \sqrt{\lambda_{i}}\) where \(\lambda_{i}\) 는 \(AA^T\) 의 eigenvalue
  • \(A^TA = V \Sigma^{T} \Sigma V^T\)
    \(V\) 는 \(A^TA\) 의 eigenvector matrix
    \(\sigma_{i} = \sqrt{\lambda_{i}}\) where \(\lambda_{i}\) 는 \(A^TA\) 의 eigenvalue
• rank and span :
  \(r = \text{rank}(A) = \text{rank}(\Sigma) \leq \text{min}(m, n)\) 에 대해
  (\(\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{r} \geq \sigma_{r+1} = \cdots = \sigma_{m} = 0\))
  • \(\text{col}(A)\) is spanned by \(\begin{bmatrix} u_1, \cdots, u_r \end{bmatrix}\)
    \(AA^Tu_i = \sigma_{i}^{2} u_i\) for \(i = 1, \cdots, r\)
  • \(\text{null}(A^T)\) is spanned by \(\begin{bmatrix} u_{r+1}, \cdots, u_m \end{bmatrix}\)
    \(AA^Tu_i = 0\) for \(i = r+1, \cdots, m\), 즉 \(A^T u_i = 0\)
  • \(\text{row}(A) = \text{col}(A^T)\) is spanned by \(\begin{bmatrix} v_{1}^{T}, \cdots, v_{r}^{T} \end{bmatrix}\)
    \(A^TAv_i = \sigma_{i}^{2} v_i\) for \(i = 1, \cdots, r\)
  • \(\text{null}(A)\) is spanned by \(\begin{bmatrix} v_{r+1}^{T}, \cdots, v_{n}^{T} \end{bmatrix}\)
    \(A^TAv_i = 0\) for \(i = r+1, \cdots, n\), 즉 \(A v_i = 0\)
  • \(A = U \Sigma V^T\) \(\rightarrow\) \(A V = U \Sigma\)
    \(A v_i = \sigma_{i} u_i\) for \(i = 1, \cdots, r\)
    \(A v_i = 0\) for \(i = r+1, \cdots, n\)

• SVD (rank에 맞게 줄인 버전) :
  \(A = \begin{bmatrix} u_1 & u_2 & \cdots & u_r \end{bmatrix} \begin{bmatrix} \sigma_{1} & 0 & \cdots & 0 \\ 0 & \sigma_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \sigma_{r} \end{bmatrix} \begin{bmatrix} v_1^{T} \\ v_2^{T} \\ \vdots \\ v_r^{T} \end{bmatrix}\)
  \(= \sum_{i=1}^{r} \sigma_{i} u_i v_{i}^{T}\)

• Eigen Decomposition :
  matrix \(A\) 가 square and real and symmetric일 경우
  \(A P = P D\)
  where \(P\) is orthonormal eigenvector matrix (\(P^{-1} = P^T\) and \(PP^T = I\))
  where \(D\) is diagonal eigenvalue matrix

• SVD 계산 과정 Summary :
  • Step 1)
    \(A^TA\) 를 Eigen Decomposition해서,
    eigenvector matrix \(V\) 와 eigenvalue matrix \(\Sigma\) 를 구함
    이 때, \(\Sigma\) 의 singular value는 \(A^TA\) 의 eigenvalue에 \(\sqrt{\cdot}\) 씌워서 구함
  • Step 2)
    eigenvector matrix \(V\) 의 columns를 normalize하고
    \(V^TV=I\) 맞는지 확인
  • Step 3)
    \(Av_i = \sigma_{i} u_i\), 즉 \(u_i = \sigma_{i}^{-1} A v_i\) 으로
    eigenvector \(u_i\) 구하고
    normalize해서 \(UU^T = I\) 맞는지 확인
  • Step 4)
    \(A = U \Sigma V^T\) 맞는지 최종 확인
• Relation b.w. PCA and SVD :
  matrix \(A\) 의 columns가 zero-mean centered일 때
  • PCA :
    covariance matrix \(C = E[AA^T] = \frac{1}{N-1}AA^T\)의 eigenvectors를 구한 뒤
    eigenvalue 큰 순으로 잘라서 principal eigenvectors의 합으로 표현
  • SVD :
    \(AA^T = U \Sigma^{2} U^T = V \Sigma^{2} V^T\) (\(U = V\) since \(AA^T\) is square matrix) 이므로
    \(AA^T\)의 eigenvector matrix \(V\) 를 구한 뒤
    rank \(r \leq \text{min}(m, n)\)에 맞게 줄여서 \(A = U \Sigma V^T = \sum_{i=1}^{r} \sigma_{i} u_i v_{i}^{T}\) 로 표현
  • Relation :
    둘은 mathematically 동일!
    \(C = V \frac{\Sigma^{2}}{N-1} V^T\)

Chapter 4. Non-parametric Techniques

• parametric approach :
  pdf가 어떤 form인지 미리 알아야 함
  e.g. \(N(\mu, \Sigma)\) 의 \(\mu\) 를 estimate
  하지만 실제로는 pdf prior form 모를 때가 많다
  • 해결 방법 1)
    Non-parametric approach로 samples로부터 pdf (density \(\hat p(x) \approx p(x)\)) 를 직접 estimate
    e.g. Parzen window
    e.g. k-NN
  • 해결 방법 2)
    아예 posterior를 직접 estimate
    e.g. Direct Decision Rule - Nearest-Neighbor

Density Estimation

• \(P(x \in R) = \int_{R} p(x)dx\) :
  pdf \(p(x)\) 를 안다면 위의 식으로 a sample \(x\) 가 region \(R\) 안에 속할 확률을 구할 수 있다
  But, pdf 모를 때는?
  • \(P \approx \frac{k}{n}\)
    where \(n\) 개의 samples 중 region \(R\) 안에 속하는 samples가 \(k\)개
  • For very small region \(R\),
    \(P(x \in R) \approx \hat p(x) \cdot V\)
    where V is volume enclosed by \(R\)
  • 즉, \(\hat p(x) = \frac{k/n}{V}\) is pdf estimator of \(p(x)\)
    • case 1) fixed V (volume of region \(R\) is fixed)
      sample 수 많아지면 \(\text{lim}_{n \rightarrow \infty} k/n = P\) 로 수렴
      So, \(\hat p(x)\) is averaged ver. of \(p(x)\)
    • case 2) \(V \rightarrow 0\) (volume of region \(R\) shrinks to 0)
      region \(R\)의 volume이 매우 작으므로 \(k \rightarrow 0\)
      So, \(p(x)\) 는 zero에 가깝고, \(\hat p(x)\) 는 very noisy
    • case 3) 실제 상황
      sample 수 \(n\) is limited
      volume \(V\) 는 arbitrarily small일 수 없음
      따라서 samples에 따라 \(\frac{k}{n}\)과 averaging by \(V\) 에 어느 정도 variance가 있음
  • \(\hat p(x)\) 가 \(p(x)\) 로 converge하려면 아래의 세 가지 조건 만족해야 함
    • \(\text{lim}_{n \rightarrow \infty} V = 0\)
      no averaging in the limit
    • If \(V\) is fixed, \(\text{lim}_{n \rightarrow \infty} k = \infty\)
      그래야 \(\frac{k/n}{V}\) 가 probability \(p(x)\) 로 수렴
      만약 \(\text{lim}_{n \rightarrow \infty} k = c\) 라면 \(\text{lim}_{n \rightarrow \infty} \hat p(x) = 0\)
    • \(\text{lim}_{n \rightarrow \infty} \frac{k}{n} = 0\)
      So, \(\text{lim}_{n \rightarrow \infty} \hat p(x) = \text{lim}_{n \rightarrow \infty} \frac{k/n}{V}\) is density function
  • \(\text{lim}_{n \rightarrow \infty} \hat p(x) = p(x)\) 위해
    • e.g. \(V = \frac{V_0}{\sqrt{n}}\) (Parzen window method)
      so that \(\text{lim}_{n \rightarrow \infty} V = 0\)
    • e.g. \(k = \sqrt{n}\)
      so that \(\text{lim}_{n \rightarrow \infty} k = \infty\) and \(\text{lim}_{n \rightarrow \infty} \frac{k}{n} = 0\) and \(\text{lim}_{n \rightarrow \infty} V = \text{lim}_{n \rightarrow \infty} \frac{\sqrt{n}}{n \hat p(x)} = 0\)

Density Estimation - Parzen window

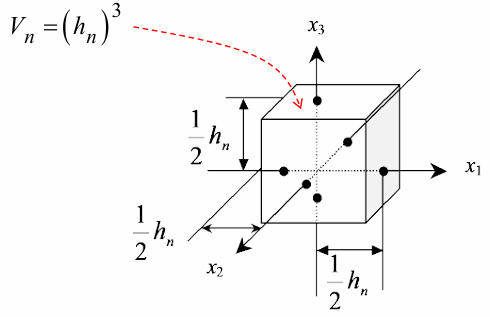
• Let’s define Parzen window as unit hypercube
  \(\phi (u) = \begin{cases} 1 & \text{if} & | u_i | \leq \frac{1}{2} \\ 0 & \text{O.W.} \end{cases}\) for \(i = 1, \ldots, d\)

• \(\phi (u)\) 는 indicator function처럼 쓰여서
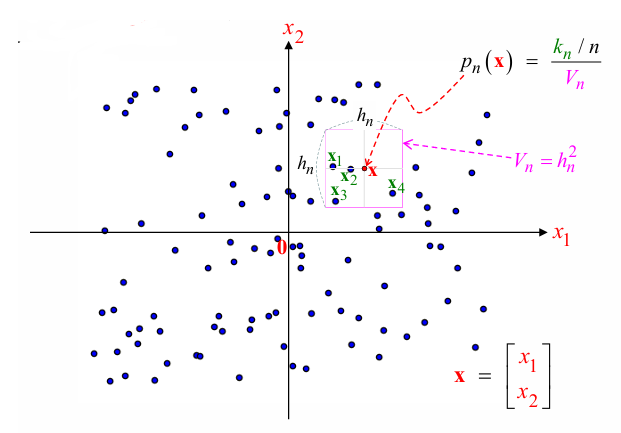
  \(x\) 를 중심으로 하고 \((h_n)^d\) 의 범위를 갖는 cube 안에 들어오는 sample 개수 \(k\) 를 세는 데 사용
  • \(k = \sum_{i=1}^n \phi (\frac{x - x_i}{h_n})\) and \(V = (h_n)^d\)
    \(\rightarrow\)
    \(\hat p(x) = \frac{k/n}{V} = \frac{1}{n} \sum_{i=1}^n \frac{\phi (\frac{x - x_i}{h_n})}{(h_n)^d}\) :
    interpolated function at position \(x\) from samples \(x_i\)
• Let \(\delta_{n} (x) = \frac{1}{V} \phi (\frac{x}{h_n})\) or gaussian distribution
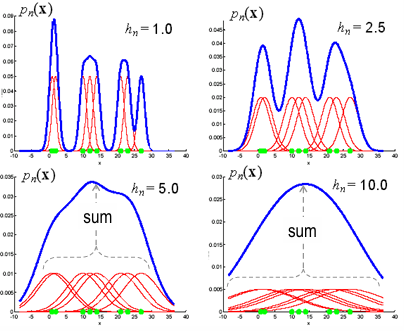
  Then \(\hat p(x) = \frac{1}{n} \sum_{i=1}^n \delta_{n} (x - x_i)\)
  • \(h_n\) (\(V\)) 이 클 경우 :
    \(\delta_{n}(x)\) 의 variance가 커서
    이를 합친 \(\hat p(x) = \frac{1}{n} \sum_{i=1}^n \delta_{n} (x - x_i)\) 는 오히려 smoothed ver. of \(p(x)\) at \(x\)
    (too little resolution)
  • \(h_n\) (\(V\)) 이 작을 경우 :
    \(\delta_{n}(x)\) 의 variance가 작아서
    이를 합친 \(\hat p(x) = \frac{1}{n} \sum_{i=1}^n \delta_{n} (x - x_i)\) 는 noisy estimate of \(p(x)\) (variation이 큼)
    (too much statistical variation)

• 만약 \(h_n \rightarrow 0\) (\(\text{lim}_{n \rightarrow \infty} V = 0\)) 이라면
  • \(\text{lim}_{n \rightarrow \infty} \delta_{n} (x) = \delta (x)\) (Dirac delta func.)
  • \(\text{lim}_{n \rightarrow \infty} E[\hat p(x)] = \text{lim}_{n \rightarrow \infty} \frac{1}{n} \sum_{i=1}^n E_{x_i}[\frac{1}{V} \phi (\frac{x - x_i}{h_n})]\)
    \(= \text{lim}_{n \rightarrow \infty} \frac{1}{n} \cdot n \cdot \int \frac{1}{V} \phi (\frac{x - s}{h_n}) p(s) ds\)
    \(= \text{lim}_{n \rightarrow \infty} \frac{1}{V} \phi(\frac{x}{h_n}) \ast p(x)\) by definition of convolution
    \(= \text{lim}_{n \rightarrow \infty} \delta_{n}(x) \ast p(x)\)
    \(= \delta (x) \ast p(x)\)
    \(= p(x)\)

Density Estimation - kNN method

• 고정된 \(k_n\) 값에 대해
  \(k_n\) nearest neighbors 찾을 때까지 \(V_n\) expand
  \(\rightarrow\)
  training samples가 sparse한 곳에서 \(\hat p(x) \rightarrow 0\) 인 걸 방지

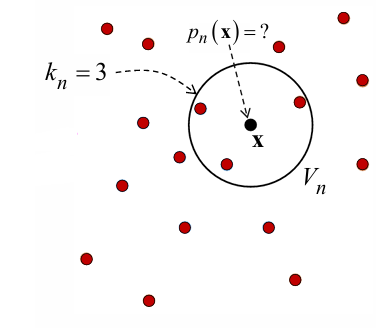
• k-NN estimation :
  probability \(\frac{k}{n}\) 은 고정하고
  \(k\)-개의 sample이 들어 있는 volume \(V\) 의 크기를 통해 density estimation

Classification based on Parzen-window and k-NN

• classification based on Parzen-window method :
  • density estimate
    \(\hat p(x) = \frac{1}{n} \sum_{i=1}^n (\frac{1}{V_n} \phi (\frac{x-x_i}{h_n}))\)
  • classification
    choose \(w_1\)
    if \(\frac{\hat p(x | w_1)}{\hat p(x | w_2)} = \frac{\frac{1}{n_1} \sum_{i=1}^{n_1} (\frac{1}{V_{n_1}} \phi (\frac{x-x_i}{h_n}))}{\frac{1}{n_2} \sum_{i=1}^{n_2} (\frac{1}{V_{n_2}} \phi (\frac{x-x_i}{h_n}))} \gt \frac{(\lambda_{12} - \lambda_{22})P(w_2)}{(\lambda_{21} - \lambda_{11})P(w_1)}\)
• classification based on k-NN method :
  • density estimate
    \(\hat p(x) = \frac{k_n / n}{V_n}\)
  • classification
    choose \(w_1\)
    if \(\frac{\hat p(x | w_1)}{\hat p(x | w_2)} = \frac{\frac{k_1 / n_1}{V_{n_1}}}{\frac{k_2 / n_2}{V_{n_2}}} \gt \frac{(\lambda_{12} - \lambda_{22})P(w_2)}{(\lambda_{21} - \lambda_{11})P(w_1)}\)
    if \(\frac{V_{n_2}}{V_{n_1}} \gt \frac{n_1(\lambda_{12} - \lambda_{22})P(w_2)}{n_2(\lambda_{21} - \lambda_{11})P(w_1)}\)
    (\(k_1 = k_2\) is fixed for k-NN)

Direct Estimation of Posteriori

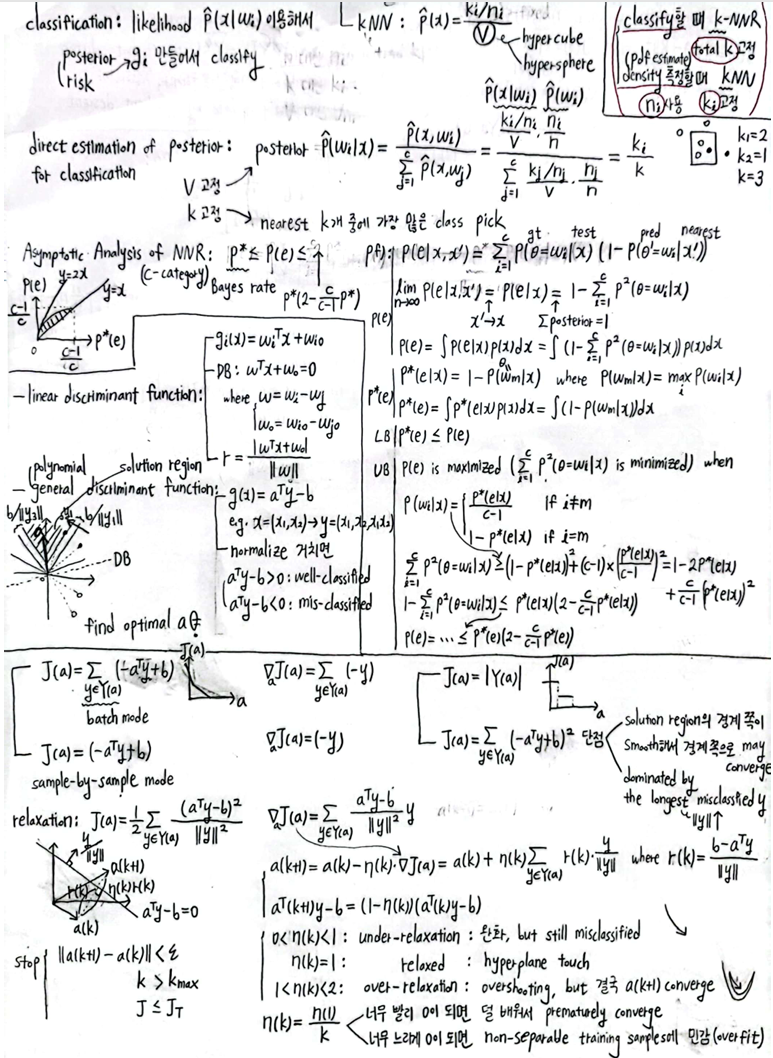
• NNR (Nearest Neighbor Rule) :
  • Step 1)
    estimate posteriori \(\hat P(w_i | x)\) directly from training set
    • classify하고 싶은 data \(x\) 를 중심으로 volume \(V\) 둠
    • likelihood pdf \(\hat P(x | w_i) = \frac{k_i / n_i}{V}\)
      where \(n_i\) : 총 \(n\) samples 중 class \(w_i\) 에 속하는 samples 수
      where \(k_i\) : \(V\) 안에 속하는 \(k\) samples 중 class \(w_i\) 에 속하는 samples 수 (\(\sum_{i=1}^c k_i = k\))
    • class probability \(\hat P(w) = \frac{n_i}{n}\)

    • joint pdf $$\hat P (x, w_{i}) = \hat P (x

      w_{i}) \hat P (w_{i}) = \frac{k_{i}/n}{V}$$

    • posterior $$\hat P (w_{i}

      x) = \frac{\hat P (x, w_{i})}{\sum_{j=1}^c \hat P(x, w_{j})} = \frac{(k_{i}/n) / V}{\sum_{j=1}^c (k_{j} / n) / V} = \frac{k_{i}}{k}$$

  • Step 2)
    classification based on estimated \(\hat P(w_i | x)\)

    • choose \(w_i\) where $$i = \text{argmax}{i} \hat P (w{i}

      x) = \text{argmax}{i} k{i}$$

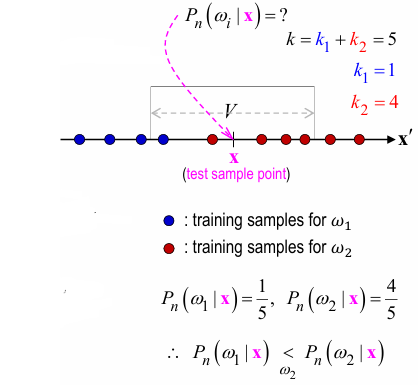
• k-NNR :
  volume \(V\) 를 고정하는 게 아니라 \(V\) 에 속하는 sample 수 \(k\) 를 고정
  • 1-NNR :
    assign test sample \(x\) to the same class as the nearest training sample \(x^{'}\)
  • 3-NNR :
    assign test sample \(x\) to the class where the nearest training samples 3개 중 2개 이상이 속한 class
  • k-NNR :
    무승부 방지 위해 \(k\) 는 항상 홀수로 설정

Asymptotic Analysis of NNR

• Error Bound for NNR (Nearest Negibor Rule) :
  • probability of error :
    • exact :
      \(P(e) = \int (1 - \sum_{i=1}^c P^2(w_i | x)) p(x)dx\)
    • approximate :
      if all \(c\) classes have equal probability
      \(P(e) = 1 - \frac{1}{c}\)
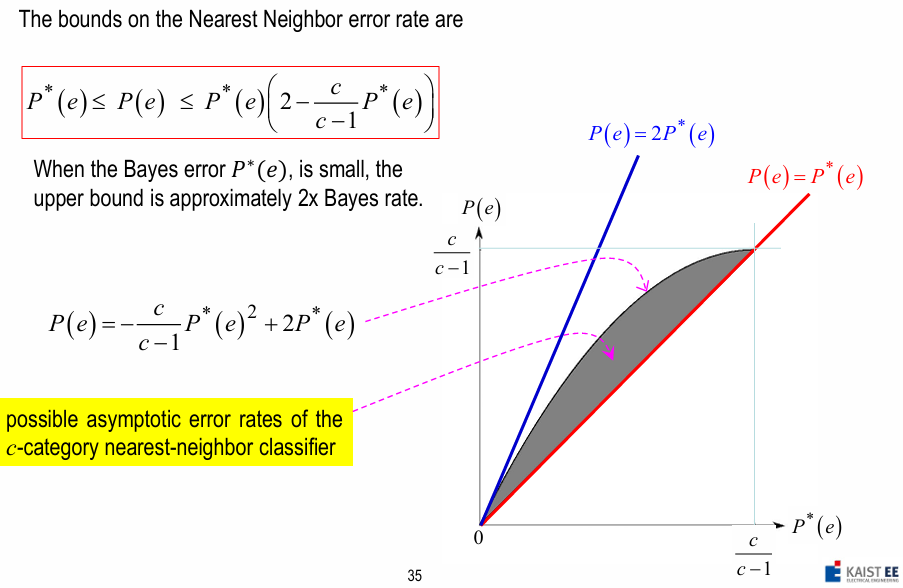
  • error bound :
    \(P^{\ast} \leq P(e) \leq 2 P^{\ast}\)
    for Bayes rate \(P^{\ast}\)

증명해보자

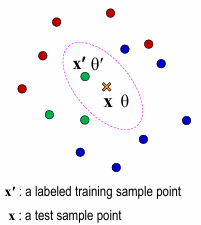
• Asymptotic Error Rate of NNR :
  Let \(x\) be test data
  Let \(x^{'}\) be the nearest neighbor for 1-NNR
  Let \(\theta^{'}\) be the labeled class of \(x^{'}\) (pred)
  Let \(\theta\) be the true class (gt)
  • Define \(P(e)\) and \(P^{\ast}(e)\) :
    • Step 1-1)
      \(P(e|x, x^{'}) = \sum_{i} P(\theta = w_i, \theta^{'} \neq w_i|x, x^{'}) = \sum_{i} P(\theta = w_i|x) P(\theta^{'} \neq w_i|x^{'}) = \sum_{i} P(\theta = w_i|x) (1 - P(\theta^{'} = w_i|x^{'}))\)
      • As \(n \rightarrow \infty\), \(x^{'} \rightarrow x\)
        So, \(\text{lim}_{n \rightarrow \infty} P(\theta^{'} = w_i | x^{'}) = P(\theta = w_i | x)\)
    • Step 1-2)
      \(\text{lim}_{n \rightarrow \infty} P(e | x, x^{'}) = P(e | x) = \text{lim}_{n \rightarrow \infty} \sum_{i} P(\theta = w_i | x) (1 - P(\theta^{'} = w_i | x^{'})) = \sum_{i} P(\theta = w_i | x) (1 - P(\theta = w_i | x)) = \sum_{i} P(\theta = w_i | x) - \sum_{i} (P(\theta = w_i | x))^2 = 1 - \sum_{i} (P(\theta = w_i | x))^2\)
    • Step 1-3)
      \(P(e) = \int P(e|x) p(x) dx = \int (1 - \sum_{i}^c (P(\theta = w_i | x))^2) p(x) dx\)
      Here, \(\sum_{i}^c (P(\theta = w_i | x))^2\) is maximized when
    • Step 2-1)
      Let \(P^{\ast}(e | x)\) be the minimum value of \(P(e|x)\)
      Then \(P^{\ast}(e | x) = 1 - P(w_m | x)\)
      where \(P(w_m | x) = \text{max}_{i} P(w_i | x)\)
    • Step 2-2)
      \(P^{\ast}(e)\) :
      \(P^{\ast}(e) = \int P^{\ast}(e | x) p(x) dx = \int (1 - P(w_m | x)) p(x) dx\)
  • Lower Bound of \(P(e)\) :
    • 정의한대로
      \(P^{\ast}(e) \leq P(e)\)
  • Upper Bound of \(P(e)\) :
    • \(P(e)\) is maximized
      (\(\sum_{i}^c (P(\theta = w_i | x))^2\) is minimized)
      when 가장 높은 확률의 class \(w_m\) 빼고는 posterior 확률이 같을 때
      as \(P(w_i | x) = \begin{cases} \frac{P^{\ast}(e|x)}{c-1} & \text{if} & i \neq m \\ 1 - P^{\ast}(e|x) & \text{if} & i = m \end{cases}\)
    • Lower Bound of \(\sum_{i}^c (P(\theta = w_i | x))^2\) :
      \(\sum_{i}^c (P(\theta = w_i | x))^2 = P^2(w_m | x) + \sum_{i=1, i \neq m}^c P^2(w_i | x)\)
      \(\geq 1 - P^{\ast}(e|x) + (c-1)(\frac{P^{\ast}(e|x)}{c-1})^2 = 1 - 2 P^{\ast}(e|x) + \frac{c}{c-1} (P^{\ast}(e|x))^2\)
      So,
      \(1 - \sum_{i}^c (P(\theta = w_i | x))^2 \leq 2 P^{\ast}(e|x) - \frac{c}{c-1} (P^{\ast}(e|x))^2 = P^{\ast}(e|x) (2 - \frac{c}{c-1} P^{\ast}(e|x))\)
    • Upper Bound of \(P(e)\) :
      \(P(e) = \int P(e|x) p(x) dx = \int (1 - \sum_{i}^c (P(\theta = w_i | x))^2) p(x) dx \leq \int P^{\ast}(e|x) (2 - \frac{c}{c-1} P^{\ast}(e|x)) p(x) dx = P^{\ast}(e)(2 - \frac{c}{c-1} P^{\ast}(e))\)
  • Error Bounds of \(P(e)\) :
    \(P^{\ast}(e) \leq P(e) \leq P^{\ast}(e)(2 - \frac{c}{c-1} P^{\ast}(e))\)

Chapter 5. Linear Discriminant Functions

• pattern recognition :
  • Chapter 2. Bayes Decision theory :
    choose class whose posterior is maximized
    \(\rightarrow\) likelihood ratio와 threshold를 비교
    \(\rightarrow\) likelihood가 Gaussian pdf일 때의 Discriminant Functions 다룸
    (\(\Sigma_{i}\) 가 어떤 값이냐에 따라 linear or quadratic)
  • Chapter 3. Parametric approach :
    PDF form 아는 상태에서 estimate parameters
    e.g. MLE or MAP
  • Chapter 4. Non-parametric approach :
    PDF form 모르는 상태에서 estimate density
    e.g. Parzen-window or k-NN or direct estimation (NNR)
  • Chapter 5. Linear Discriminant Function :
    discriminant function form 아는 상태에서 estimate discriminant func. parameters
    (PDF form 몰라도 됨 \(\rightarrow\) Non-parametric approach)

Linear Discriminant Function

• Two-category case :
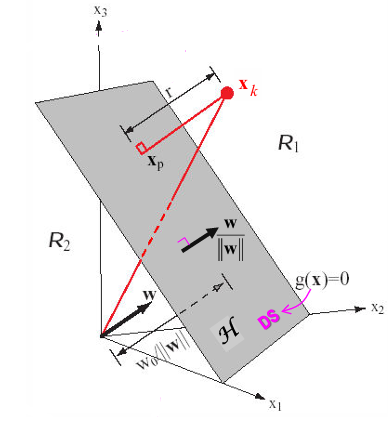
  • Decision Boundary by Linear Discriminant Function :
    \(g(\boldsymbol x) = \boldsymbol w^T \boldsymbol x + w_0 = 0\)
  • point \(\boldsymbol x = \boldsymbol x_{p} + r \frac{\boldsymbol w}{\| \boldsymbol w \|}\)
    where \(\boldsymbol x_{p}\) : projection of \(x\) onto Decision Surface
    where \(r\) : signed distance
  • signed distance :
    \(r = \frac{g(\boldsymbol x)}{\| \boldsymbol w \|} = \frac{\boldsymbol w^T \boldsymbol x + w_0}{\| \boldsymbol w \|}\)
    \(r \gt 0\) : point \(x\) is on positive side (class \(w_1\))
    \(r \lt 0\) : point \(x\) is on negative side (class \(w_2\))
    e.g. 원점에서의 거리 : \(r = \frac{w_0}{\| \boldsymbol w \|}\)

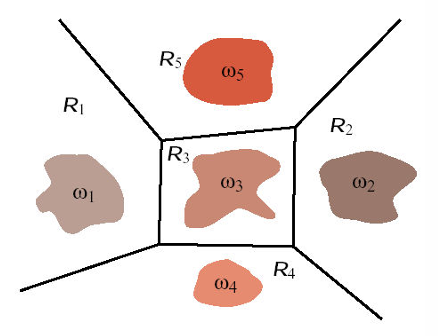
• Multi-category case :
  • \(c\)-개의 Linear Discriminant Function :
    \(g_{i}(\boldsymbol x) = \boldsymbol w_{i}^{T} \boldsymbol x + w_{i0}\) for \(i=1, \ldots, c\)
  • Decision Rule :
    class \(w_i\) if \(g_{i}(\boldsymbol x) \gt g_{j}(\boldsymbol x)\) for all \(j \neq i\)
  • \(c\)-개의 Decision Boundary by Linear Discriminant Function :
    \(g_{i}(\boldsymbol x) = g_{j}(\boldsymbol x)\) for adjacent \(i, j\)
    \(\rightarrow\) \(\boldsymbol w_{i}^{T} \boldsymbol x + w_{i0} = \boldsymbol w_{j}^{T} \boldsymbol x + w_{j0}\)
    \(\rightarrow\) \((\boldsymbol w_{i} - \boldsymbol w_{j})^{T} \boldsymbol x + (w_{i0} - w_{j0}) = 0\)
    \(\rightarrow\) \(\boldsymbol w^{T} \boldsymbol x + w_0 = 0\)
    where \(\boldsymbol w = \boldsymbol w_{i} - \boldsymbol w_{j}\) and \(w_0 = w_{i0} - w_{j0}\)
    • \(\boldsymbol w_{i} - \boldsymbol w_{j}\) :
      Decision Boundary(Hyperplane)와 수직인 vector
    • \(r = \frac{g_{i}(\boldsymbol x) - g_{j}(\boldsymbol x)}{\| \boldsymbol w_{i} - \boldsymbol w_{j} \|}\) :
      signed distance from \(\boldsymbol x\) to Decision Boundary

General Discriminant Function

• Discriminant Function :
  • Linear Discriminant Function :
    \(g(\boldsymbol x) = \boldsymbol w^T \boldsymbol x + w_0 = \sum_{i=1}^d w_{i} x_{i} + w_0\)
    e.g. likelihood \(P(x|w_i)\) 가 Gaussian PDF이고 \(\Sigma_{i}\) 가 \(\sigma^{2} I\) 또는 \(\Sigma\) 일 때
    (본 포스팅 Discriminant Function for Gaussian PDF 참고)
  • Quadratic Discriminant Function :
    \(g(\boldsymbol x) = \sum_{i=1}^d \sum_{j=1}^d w_{ij} x_{i} x_{j} + \sum_{i=1}^d w_{i} x_{i} + w_0\)
    e.g. likelihood \(P(x|w_i)\) 가 Gaussian PDF이고 \(\Sigma_{i}\) 가 arbitrary일 때
    (본 포스팅 Discriminant Function for Gaussian PDF 참고)
  • Polynomial Discriminant Function :
    \(g(\boldsymbol x) = \sum_{i=1}^{\hat d} a_i y_i(\boldsymbol x) = \boldsymbol a^{T} \boldsymbol y\)
    where \(\hat d\) : arbitrary function \(y_{i}(x)\) 개수
    e.g. 2D-to-3D : \((x_1, x_2) \rightarrow \boldsymbol y = (x_1, x_2, x_1 x_2)\)
• Two-category case (Linearly Separable) :
  • Decision Rule :
    \(g(\boldsymbol x) = \boldsymbol a^{T} \boldsymbol y\)
    \(\gt 0\) : class \(w_1\)
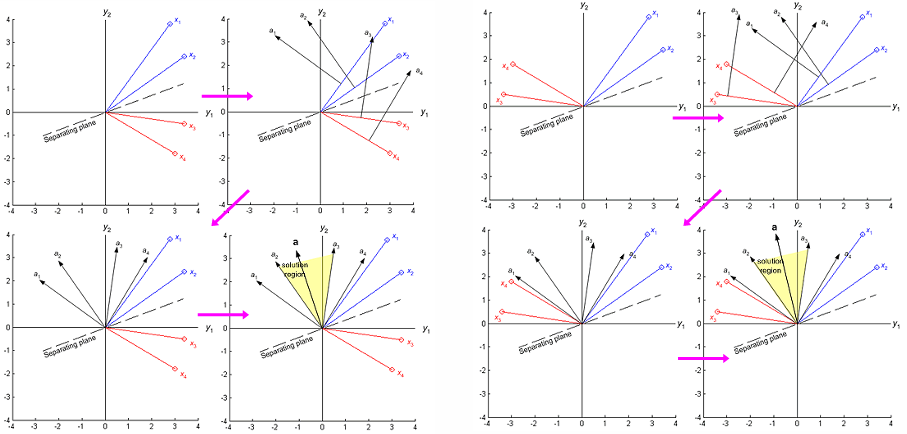
    \(\lt 0\) : class \(w_2\)
  • Solution Region of \(\boldsymbol a\) :
    training point vector와 수직인 vector들을 이용해서
    solution region 찾은 뒤
    decision boundary \(g(\boldsymbol x) = \boldsymbol a^{T} \boldsymbol y = 0\) 와 수직인 \(\boldsymbol a\) 는 해당 solution region에 속함
  • Normalize :
    이 때, class \(w_2\) 에 속하는 training points에 (-)를 곱해서 normalize 할 수 있음
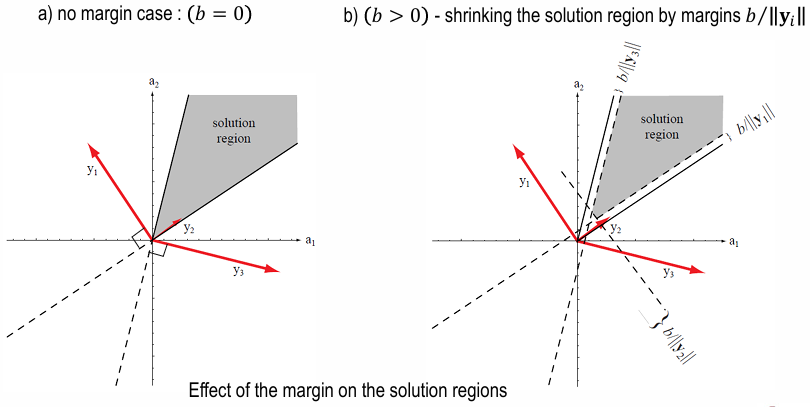
    s.t. \(\boldsymbol a^{T} \boldsymbol y \gt 0\) for both \(w_1\) and \(w_2\)
  • Solution Region of \(\boldsymbol a\) with margin \(b\) :
    Normalize했을 때
    \(\boldsymbol a^{T} \boldsymbol y \gt 0\) for both \(w_1\) and \(w_2\)
    대신
    \(\boldsymbol a^{T} \boldsymbol y \gt b \gt 0\) for both \(w_1\) and \(w_2\) 이도록
    margin을 두면
    solution region은 각 방향으로 \(\frac{b}{\| y_i \|}\) 만큼 줄어듬

class w_1 의 training points 2개와 class w_2 의 training points 2개가 있을 때, Solution Region 찾기

margin 뒀을 때, Solution Region 찾기

Gradient Descent

• Gradient Descent :
  • Solution Region 내에 있는, discriminant function \(\boldsymbol a^{T} \boldsymbol y\) 의 \(\boldsymbol a\) 를 찾기 위해
    iteratively \(\boldsymbol a\) 를 업데이트
  • \(\boldsymbol a(k+1) = \boldsymbol a(k) - \eta (k) \cdot \frac{\partial J(\boldsymbol a(k))}{\partial \boldsymbol a(k)}\)
    where \(\eta (k)\) is learning-rate
    where \(J(\boldsymbol a)\) is criterion(loss) func.

• Gradient Descent :
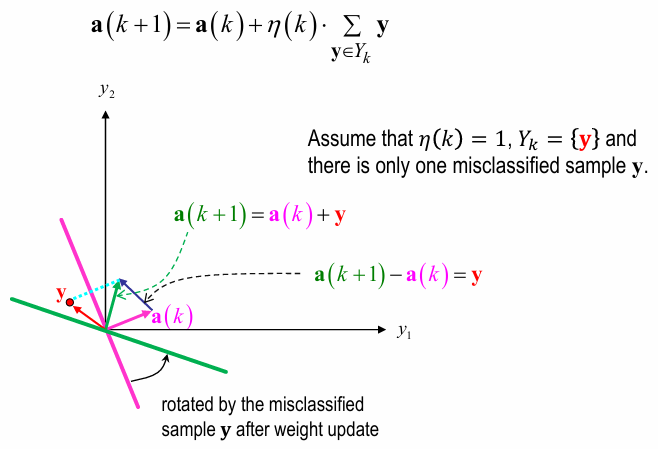
  • Loss :
    Normalize했을 경우, learnable weight vector \(\boldsymbol a\) 에 대해
    well-classified sample은 \(\boldsymbol a^{T} \boldsymbol y \gt 0\) 이고,
    misclassified sample은 \(\boldsymbol a^{T} \boldsymbol y \lt 0\) 이므로
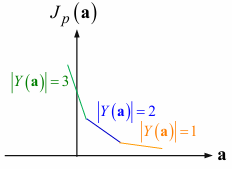
    \(J(\boldsymbol a) = \Sigma_{\boldsymbol y \in Y(\boldsymbol a)} (- \boldsymbol a^{T} \boldsymbol y)\)
    where \(Y(\boldsymbol a)\) : weight \(\boldsymbol a\) 가 잘못 분류한 sample들을 모아놓은 set
    • continuous and piece-wise linear
      (연속이지만, misclassified sample 수 바뀌는 지점에서 미분 불가능)
    • \(J(\boldsymbol a) \geq 0\)
      (Normalize했을 경우)
  • Gradient :
    \(\nabla J(\boldsymbol a(k)) = \frac{\partial J(\boldsymbol a(k))}{\partial \boldsymbol a} = \Sigma_{\boldsymbol y \in Y(\boldsymbol a)} (- \boldsymbol y)\)
  • Update :
    \(\boldsymbol a(k+1) = \boldsymbol a(k) - \eta(k) \cdot \nabla J(\boldsymbol a(k)) = \boldsymbol a(k) + \eta(k) \cdot \Sigma_{\boldsymbol y \in Y(\boldsymbol a)} (\boldsymbol y)\)
    where \(\boldsymbol y \in Y(\boldsymbol a)\) : batch
    • sample/batch :
      하나씩 update하면 sample-by-sample relaxation
      묶어서 update하면 batch relaxation

원래 분홍색 boundary일 때는 y가 아래에 있어서 misclassified이었는데, 초록색 boundary로 업데이트하면 y가 위에 있어서 well-classified

• 이외의 Loss :
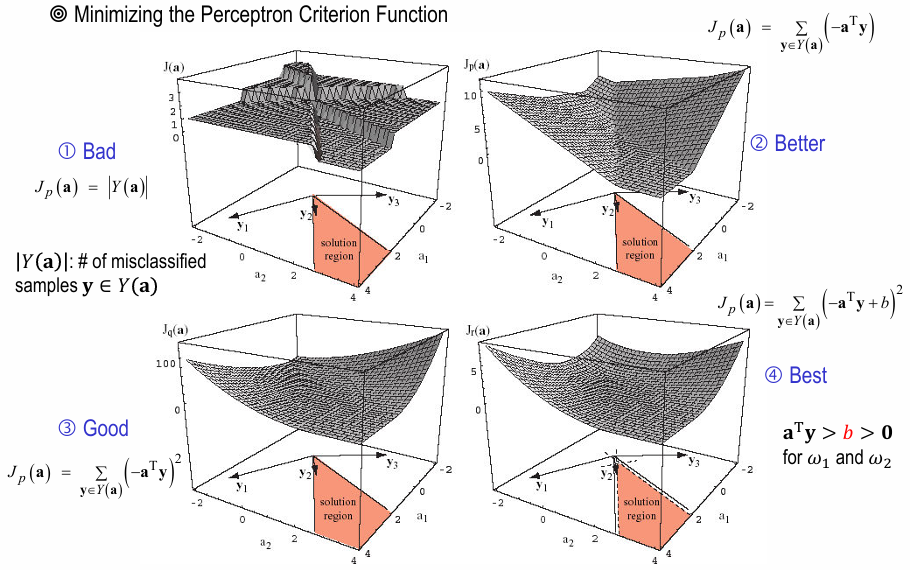
  • misclassified sample 수를 loss로 두면
    piece-wise constant여서 gradient descent에 부적합
  • \(\Sigma_{\boldsymbol y \in Y(\boldsymbol a)} (- \boldsymbol a^{T} \boldsymbol y)\) 를 loss로 두면
    piece-wise linear여서 gradient descent 가능
  • \(\Sigma_{\boldsymbol y \in Y(\boldsymbol a)} (- \boldsymbol a^{T} \boldsymbol y)^2\) 를 loss로 두면
    • 장점 : continuous gradient를 가져서 smooth loss landscape를 가지고 gradient descent에 적합
    • 단점 :
      • solution region 내 optimal weight vector \(\boldsymbol a\) 를 찾아야 하는데
        solution region의 경계 쪽이 smooth해서 경계 쪽으로 converge할 수 있음
      • dominated by the longest misclassified sample vector (\(\| \boldsymbol y \|\) 값이 매우 큰 경우)
    • 해결 :
      \(\| \boldsymbol y \|\) 값이 너무 커지는 걸 방지하는 relaxation procedure
      (아래에서 설명)
  • \(\boldsymbol a^{T} \boldsymbol y\) 대신 \(\boldsymbol a^{T} \boldsymbol y - b\) 로 margin을 두면
    better

• Relaxation procedure :
  • Loss :
    \(J(\boldsymbol a) = \frac{1}{2} \Sigma_{\boldsymbol y \in Y(\boldsymbol a)} \frac{(\boldsymbol a^{T} \boldsymbol y - b)^2}{\| \boldsymbol y \|^{2}}\)
    • penalize misclassified samples \(\boldsymbol y \in Y(\boldsymbol a)\) where \(\boldsymbol a^{T} \boldsymbol y - b \lt 0\) with margin \(b\)
  • Gradient :
    \(\nabla J(\boldsymbol a) = \frac{\partial J(\boldsymbol a)}{\partial \boldsymbol a} = \Sigma_{\boldsymbol y \in Y(\boldsymbol a)} \frac{\boldsymbol a^{T} \boldsymbol y - b}{\| \boldsymbol y \|^{2}} \boldsymbol y\)
  • Update :
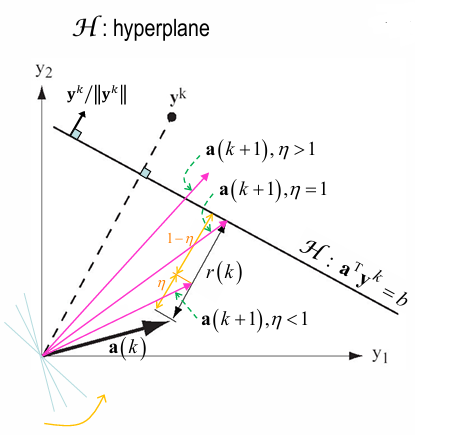
    • \(\boldsymbol a(k+1) = \boldsymbol a(k) - \eta(k) \cdot \nabla J(\boldsymbol a) = \boldsymbol a(k) + \eta(k) \cdot \Sigma_{\boldsymbol y \in Y(\boldsymbol a)} \frac{b - \boldsymbol a^{T}(k) \boldsymbol y}{\| \boldsymbol y \|^{2}} \boldsymbol y = \boldsymbol a(k) + \eta(k) \cdot \Sigma_{\boldsymbol y \in Y(\boldsymbol a)} r(k) \cdot \frac{\boldsymbol y}{\| \boldsymbol y \|}\)
      where \(r(k) = \frac{b - \boldsymbol a^{T}(k) \boldsymbol y}{\| \boldsymbol y \|}\) : distance from \(\boldsymbol a (k)\) to hyperplane \(\boldsymbol a^{T} \boldsymbol y - b = 0\)
      where \(\frac{\boldsymbol y}{\| \boldsymbol y \|}\) : unit normal vector of hyperplane \(\boldsymbol a^{T} \boldsymbol y - b = 0\)
    • 위 update 식 양변에 \(\boldsymbol y\) 를 곱해서 정리하면
      \(\boldsymbol a^{T}(k+1) \boldsymbol y - b = (1 - \eta(k)) (\boldsymbol a^{T}(k) \boldsymbol y - b)\)
    • geometric 해석 :
      \(\boldsymbol a(k+1)\) 은 \(\boldsymbol a(k)\) 를 \(\frac{\boldsymbol y}{\| \boldsymbol y \|}\) 방향으로 (hyperplane에 가까워지게)
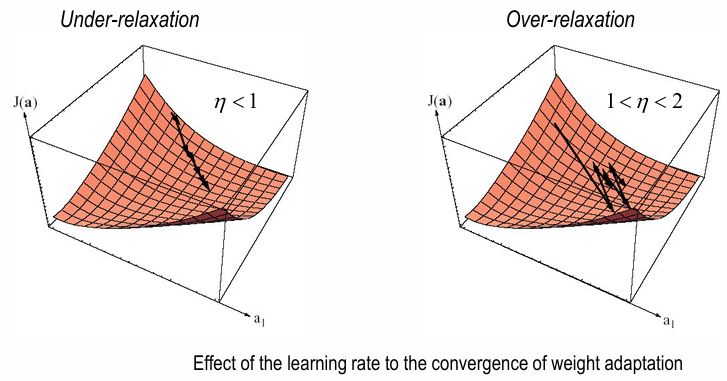
      \(\eta(k) r(k)\) 거리만큼 이동
      • \(\eta \lt 1\) : under-relaxation
        완화, but still misclassified (\(\boldsymbol a^{T} \boldsymbol y - b \lt 0\))
      • \(\eta = 1\) : relaxed
        \(\boldsymbol a(k)\) 가 hyperplane touch (\(\boldsymbol a^{T} \boldsymbol y - b = 0\))
      • \(1 \lt \eta \lt 2\) : over-relaxation
        overshooting이긴 하지만 결국 \(\boldsymbol a (k+1)\) converge
  • Stop :
    • \[\| \boldsymbol a(k+1) - \boldsymbol a(k) \| \lt \epsilon\]
    • \[k \leq k_{max}\]
    • \(J(\boldsymbol a(k)) \leq J_{T}\) since we minimize \(J(\boldsymbol a(k))\)

• Non-separable behavior :
  If \(\eta(k) \rightarrow 0\) as \(k \rightarrow \infty\),
  non-separable problems에서도 괜찮은 performance 왜???
  • \(\eta(k)\) 가 너무 빨리 0이 되면
    덜 배워서 prematurely converge (less than optimal result)
  • \(\eta(k)\) 가 너무 느리게 0이 되면
    non-separable하게 만드는 training samples에 너무 민감
  • \(\eta(k) = \frac{\eta(1)}{k}\) 로 설정하여
    \(k\) 증가 (performance 증가)할수록 learning rate \(\eta(k)\) 감소

Least Squared-Error Solution

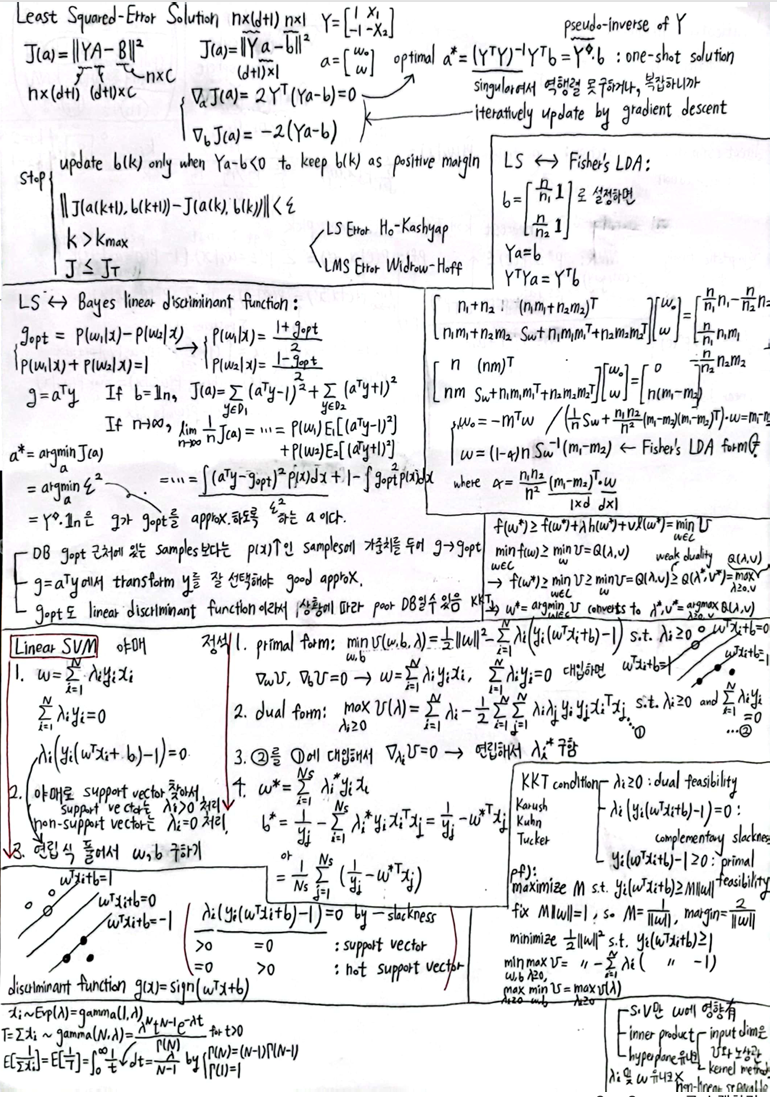
• Least Squared-Error Solution :
  • two-category :
    \(J(\boldsymbol a) = \| \boldsymbol Y \boldsymbol a - \boldsymbol b \|^{2}\)
    where \(\boldsymbol Y = \begin{bmatrix} \boldsymbol 1 & X_1 \\ - \boldsymbol 1 & - X_2 \end{bmatrix}\) : \(n \times (d+1)\) sample matrix
    where \(\boldsymbol a = \begin{bmatrix} w_0 \\ \boldsymbol w \end{bmatrix}\) : \((d+1) \times 1\) weight vector
    where \(\boldsymbol b\) : \(n \times 1\) teacher(margin) vector
    • optmize :
      \(\nabla_{\boldsymbol a} J(\boldsymbol a) = 2 \boldsymbol Y^{T} (\boldsymbol Y \boldsymbol a - \boldsymbol b) = 0\)
      \(\rightarrow\)
      optimal \(\boldsymbol a = (\boldsymbol Y^{T} \boldsymbol Y)^{-1} \boldsymbol Y^{T} \boldsymbol b = \boldsymbol Y^{\dagger} \cdot \boldsymbol b\)
      (one-shot solution)
      where \(\boldsymbol Y^{\dagger} = (\boldsymbol Y^{T} \boldsymbol Y)^{-1} \boldsymbol Y^{T}\) : pseudo-inverse of \(\boldsymbol Y\)
  • multi-category :
    \(J(\boldsymbol a) = \| \boldsymbol Y \boldsymbol A - \boldsymbol B \|^{2}\)
    where \(\boldsymbol Y\) : \(n \times (d+1)\) data matrix
    where \(\boldsymbol A\) : \((d+1) \times C\) weight vector
    where \(\boldsymbol B\) : \(n \times C\) teacher(margin) vector
    • optimize :
      optimal \(\boldsymbol A = \boldsymbol Y^{\dagger} \cdot \boldsymbol B\)
      where \(\boldsymbol Y^{\dagger} = (\boldsymbol Y^{T} \boldsymbol Y)^{-1} \boldsymbol Y^{T}\) : pseudo-inverse of \(\boldsymbol Y\)

• 이 때, \(\boldsymbol Y^{\dagger} = (\boldsymbol Y^{T} \boldsymbol Y)^{-1} \boldsymbol Y^{T}\) 에서
  \(\boldsymbol Y^{T} \boldsymbol Y\) 가 singular여서 또는 large matrix 연산 다루기 버거워서
  \((\boldsymbol Y^{T} \boldsymbol Y)^{-1}\) 를 직접 계산하기 어렵다면
  아래와 같이 iteratively update by gradient descent

• Least Squared-Error Solution (Widrow-Hoff) :
  • Loss :
    \(J(\boldsymbol a, \boldsymbol b) = \| \boldsymbol Y \boldsymbol a - \boldsymbol b \|^{2}\)
  • Gradient :
    \(\frac{\partial J(\boldsymbol a, \boldsymbol b)}{\partial \boldsymbol a} = 2 \boldsymbol Y^{T} (\boldsymbol Y \boldsymbol a - \boldsymbol b)\)
    \(\frac{\partial J(\boldsymbol a, \boldsymbol b)}{\partial \boldsymbol b} = -2 (\boldsymbol Y \boldsymbol a - \boldsymbol b)\)
  • Stop :
    • updated only when \(\boldsymbol Y \boldsymbol a - \boldsymbol b \lt 0\) to keep \(\boldsymbol b\) as positive margin
    • \[\| J(\boldsymbol a(k+1), \boldsymbol b(k+1)) - J(\boldsymbol a(k), \boldsymbol b(k)) \| \lt \epsilon\]
    • \[k \leq k_{max}\]
    • \(J(\boldsymbol a(k), \boldsymbol b(k)) \leq J_{T}\) since we minimize \(J\)
• Least Squared-Error와 Fisher’s Linear Discriminant Function의 관계 :
  • \(J(\boldsymbol a) = \| \boldsymbol Y \boldsymbol a - \boldsymbol b \|^{2}\)
    where \(\boldsymbol Y = \begin{bmatrix} \boldsymbol 1 & X_1 \\ - \boldsymbol 1 & - X_2 \end{bmatrix}\) : \(n \times (d+1)\) data matrix
    where \(\boldsymbol a = \begin{bmatrix} w_0 \\ \boldsymbol w \end{bmatrix}\) : \((d+1) \times 1\) weight vector
    where \(\boldsymbol b = \begin{bmatrix} \frac{n}{n_1} \boldsymbol 1 \\ \frac{n}{n_2} \boldsymbol 1 \end{bmatrix}\) : \(n \times 1\) teacher(margin) vector
    (\(\boldsymbol b\) 를 위와 같이 설정함으로써 LSE와 Fisher’s LDA의 Relation 설명 가능!)
  • \(\boldsymbol Y \boldsymbol a = \boldsymbol b\)
    \(\boldsymbol Y^T \boldsymbol Y \boldsymbol a = \boldsymbol Y^T \boldsymbol b\)
    \(\begin{bmatrix} \boldsymbol 1^T & - \boldsymbol 1^T \\ X_{1}^{T} & - X_{2}^{T} \end{bmatrix} \begin{bmatrix} \boldsymbol 1 & X_1 \\ - \boldsymbol 1 & - X_2 \end{bmatrix} \begin{bmatrix} w_0 \\ \boldsymbol w \end{bmatrix} = \begin{bmatrix} \boldsymbol 1^T & - \boldsymbol 1^T \\ X_{1}^{T} & - X_{2}^{T} \end{bmatrix} \begin{bmatrix} \frac{n}{n_1} \boldsymbol 1 \\ \frac{n}{n_2} \boldsymbol 1 \end{bmatrix}\)
    \(\begin{bmatrix} n_{1} + n_{2} & (n_{1} \boldsymbol m_{1} + n_{2} \boldsymbol m_{2})^{T} \\ n_{1} \boldsymbol m_{1} + n_{2} \boldsymbol m_{2} & S_w + n_{1} \boldsymbol m_{1} \boldsymbol m_{1}^{T} + n_{2} \boldsymbol m_{2} \boldsymbol m_{2}^{T} \end{bmatrix} \begin{bmatrix} w_0 \\ \boldsymbol w \end{bmatrix} = \begin{bmatrix} \frac{n}{n_1} n_{1} - \frac{n}{n_2} n_{2} \\ \frac{n}{n_1} n_1 \boldsymbol m_{1} - \frac{n}{n_2} n_2 \boldsymbol m_{2} \end{bmatrix}\)
    \(\begin{bmatrix} n & (n \boldsymbol m)^{T} \\ n \boldsymbol m & S_w + n_{1} \boldsymbol m_{1} \boldsymbol m_{1}^{T} + n_{2} \boldsymbol m_{2} \boldsymbol m_{2}^{T} \end{bmatrix} \begin{bmatrix} w_0 \\ \boldsymbol w \end{bmatrix} = \begin{bmatrix} 0 \\ n(\boldsymbol m_{1} - \boldsymbol m_{2}) \end{bmatrix} \cdots (\ast)\)
    ??? 가장 왼쪽 matrix의 (2, 2) 항이 왜 저렇게 나옴 ???
  • \(\ast\) 의 first row를 정리하면
    \(w_0 = - \boldsymbol m^{T} \boldsymbol w\)
    where \(\boldsymbol m = \frac{n_{1} \boldsymbol m_{1} + n_{2} \boldsymbol m_{2}}{n}\) : mean of all samples
  • 위의 식과 \(\boldsymbol m = \frac{n_{1} \boldsymbol m_{1} + n_{2} \boldsymbol m_{2}}{n}\) 를 이용해서
    \(\ast\) 의 second row를 정리하면
    \((\frac{1}{n} S_w + \frac{n_{1} n_{2}}{n^{2}} (\boldsymbol m_{1} - \boldsymbol m_{2}) (\boldsymbol m_{1} - \boldsymbol m_{2})^{T}) \cdot \boldsymbol w = \boldsymbol m_{1} - \boldsymbol m_{2}\)
    \(\frac{1}{n} S_w \cdot \boldsymbol w + \frac{n_{1} n_{2}}{n^{2}} (\boldsymbol m_{1} - \boldsymbol m_{2}) (\boldsymbol m_{1} - \boldsymbol m_{2})^{T} \cdot \boldsymbol w = \boldsymbol m_{1} - \boldsymbol m_{2}\)
    \(\frac{1}{n} S_w \cdot \boldsymbol w = (1 - \alpha) (\boldsymbol m_{1} - \boldsymbol m_{2})\)
    where constant \(\alpha = \frac{n_{1} n_{2}}{n^{2}} k\)
    where constant \(k = (\boldsymbol m_{1} - \boldsymbol m_{2})^{T} \cdot \boldsymbol w = (1 \times d)(d \times 1) = (1 \times 1)\)
    So, \(\boldsymbol w = (1 - \alpha) n S_{w}^{-1} (\boldsymbol m_{1} - \boldsymbol m_{2})\)
    이는 Fisher’s LDA (\(\boldsymbol w = q S_{w}^{-1} (\boldsymbol m_{1} - \boldsymbol m_{2})\)) 와 same!!

• discriminant function :
  • Bayes linear discriminant function :
    \(g_{opt} = P(w_{1} | \boldsymbol x) - P(w_{2} | \boldsymbol x)\)
    \(P(w_{1} | \boldsymbol x) + P(w_{2} | \boldsymbol x) = 1\)
    \(P(w_{1} | \boldsymbol x) = \frac{1 + g_{opt}}{2}\) and \(P(w_{2} | \boldsymbol x) = \frac{1 - g_{opt}}{2}\)
  • LS-based linear discriminant function :
    \(g = \boldsymbol a^{T} \boldsymbol y\)
    • If \(\boldsymbol b = \boldsymbol 1_{n}\),
      \(J_{s}(\boldsymbol a) = \sum_{\boldsymbol y \in D_{1}} (\boldsymbol a^{T} \boldsymbol y - 1)^{2} + \sum_{\boldsymbol y \in D_{2}} (\boldsymbol a^{T} \boldsymbol y + 1)^{2}\)
      \(\rightarrow\)
      \(J(\boldsymbol a) = \text{lim}_{n \rightarrow \infty} \frac{1}{n} J_{s}(\boldsymbol a) = \cdots = P(w_1) E_{1}[(\boldsymbol a^{T} \boldsymbol y - 1)^{2}] + P(w_2) E_{2}[(\boldsymbol a^{T} \boldsymbol y + 1)^{2}] = \cdots = \int (\boldsymbol a^{T} \boldsymbol y - g_{opt}(\boldsymbol x))^{2} p(\boldsymbol x) dx + 1 - \int g_{opt}^{2}(\boldsymbol x) p(\boldsymbol x) dx\)
      \(= \epsilon^{2} + 1 - \int g_{opt}^{2}(\boldsymbol x) p(\boldsymbol x) dx\)
      where MSE \(\epsilon^{2} = \int (g - g_{opt})^{2} p(\boldsymbol x) dx\)
      \(\rightarrow\)
      \(1 - \int g_{opt}^{2}(\boldsymbol x) p(\boldsymbol x) dx\) 는 \(\boldsymbol a\) 와 무관한 term이기 때문에
      optimal \(\boldsymbol a = \text{argmin}_{\boldsymbol a} J(\boldsymbol a) = \text{argmin}_{\boldsymbol a} \epsilon^{2}\)
  • 정리하면,
    \(\boldsymbol b = \boldsymbol 1_{n}\) and \(n \rightarrow \infty\) 일 때
    optimal \(\boldsymbol a = \boldsymbol Y^{\dagger} \boldsymbol 1_{n}\) 에 대해
    LS-based linear discrimant function \(g(\boldsymbol x) = \boldsymbol a^{T} \boldsymbol y\) 은
    Bayes linear discrimant function \(g_{opt}(\boldsymbol x) = P(w_{1} | \boldsymbol x) - P(w_{2} | \boldsymbol x)\) 을
    approx.한다
  • remark :
    • decision boundary \(g_{opt}\) 근처에 있는 samples보다는 ???
      high probability \(p(\boldsymbol x)\) 를 가지는 samples에 가중치를 두어 LS-based solution이 Bayes에 가까워지도록 함
    • \(g = \boldsymbol a^{T} \boldsymbol y\) 에서 \(\boldsymbol x\) 의 transform (\(\boldsymbol y\)) 를 얼마나 잘 선택하느냐에 따라 approx. 퀄이 달라짐
    • linear discriminant function이라서 상황에 따라 \(g_{opt}\) 도 poor decision boundary를 가질 수 있음

Linear Support Vector Machine (Linear SVM)

• Lagrange Dual Problem :
  • Minimize \(f(w)\) s.t. \(h(w) \leq 0\) and \(l(w) = 0\)
    \(\rightarrow\)
    Lagrange function \(L(w, \lambda, v) = f(w) + \lambda h(w) + v l(w)\)
    \(\rightarrow\)
    optimal solution \(w^{\ast} = \text{argmin}_{w \in C} L(w, \lambda, v)\)
    where feasible region \(C = \{ w | h(w) \leq 0, l(w) = 0 \}\)
  • Eq 1.
    \(f(w^{\ast}) \geq f(w^{\ast}) + \lambda h(w^{\ast}) + v l(w^{\ast}) = \text{min}_{w \in C} L(w, \lambda, v)\)
  • Eq 2.
    \(\text{min}_{w \in C} f(w) \geq \text{min}_{w} L(w, \lambda, v) = Q(\lambda, v)\)
    즉, minimize해야 되는 상황에서 solution in feasible region \(\geq\) solution in global region
  • Eq 1., 2. 합치면
    \(f(w^{\ast}) \geq \text{min}_{w \in C} L(w, \lambda, v) \geq \text{min}_{w} L(w, \lambda, v) = Q(\lambda, v) \geq Q(\lambda^{\ast}, v^{\ast}) = \text{max}_{\lambda \geq 0, v} Q(\lambda, v)\)
  • duality :
    • weak duality :
      \(f(w^{\ast}) \geq Q(\lambda^{\ast}, v^{\ast})\)
    • strong duality under Slater’s condition :
      \(f(w^{\ast}) = Q(\lambda^{\ast}, v^{\ast})\)
  • KKT (Karush-Kuhn-Tucker) condition :
    KKT condition 만족 if and only if Slater’s condition 만족
    • \[\frac{\partial L(w, \lambda, v)}{\partial w} = 0\]
    • \[\frac{\partial L(w, \lambda, v)}{\partial v} = 0\]
    • \(\lambda h(w) \leq 0\) (complementary slackness condition)
    • \(v l(w) = 0\) (primal feasibility condition)
    • \(\lambda \geq 0\) (dual feasibiliity condition)
  • Summary :
    만약 KKT condition을 만족해서 Slater’s condition을 만족할 경우
    strong duality가 성립해서 \(f(w^{\ast}) = L(w^{\ast}, \lambda^{\ast}, v^{\ast}) = Q(\lambda^{\ast}, v^{\ast})\) 이므로
    \(\rightarrow\)
    Primal Problem : \(w^{\ast} = \text{argmin}_{w \in C} L(w, \lambda, v)\)
    s.t. \(C = \{ w | h(w) \leq 0, l(w) = 0 \}\)
    \(\rightarrow\)
    Dual Problem : \(\lambda^{\ast}, v^{\ast} = \text{argmax}_{\lambda \geq 0, v} Q(\lambda, v)\)
    s.t. \(\lambda \geq 0\)
• Linear SVM decision rule (hard margin) :
  • discriminant function :
    discriminant function \(g(\boldsymbol x) = \text{sign}(\boldsymbol w^{T} \boldsymbol x + b)\)
  • decision boundary :
    decision boundary \(\boldsymbol w^{T} \boldsymbol x + b = 0\) that maximizes the margin
  • margin :
    margin \(M = \text{min}_{\boldsymbol x \in D} d(\boldsymbol x) = \text{min}_{\boldsymbol x \in D} \frac{| \boldsymbol w^{T} \boldsymbol x + b |}{\| \boldsymbol w \|}\)
    where margin은 support vectors(extreme vectors)가 결정
  • goal :
    \(\text{max}_{\boldsymbol w, b} M = \text{max}_{\boldsymbol w, b} \text{min}_{\boldsymbol x \in D} d(\boldsymbol x) = \text{max}_{\boldsymbol w, b} \text{min}_{\boldsymbol x \in D} \frac{| \boldsymbol w^{T} \boldsymbol x + b |}{\| \boldsymbol w \|}\)
    • primal form :
      \(y_{i} = 1\) if \(x_{i} \in\) class \(w_{1}\) and \(y_{i} = -1\) if \(x_{i} \in\) class \(w_{2}\) 에 대해
      maximize \(M\) s.t. \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) \geq M \| \boldsymbol w \|\)
      \(\rightarrow\)
      Since we can arbirarily scale \(\boldsymbol w\) and \(b\),
      fix \(M \| \boldsymbol w \| = 1\) so that \(M = \frac{1}{\| \boldsymbol w \|}\) and \(g(\boldsymbol x) = \pm 1\) for support vector \(\boldsymbol x\)
      \(\rightarrow\)
      minimize \(\frac{1}{2}\| \boldsymbol w \|^{2}\) s.t. \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) \geq 1\)
    • Lagrange Multiplier Method :
      minimize \(\frac{1}{2}\| \boldsymbol w \|^{2}\) s.t. \(g_{i} = y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) - 1 \geq 0\)
      \(\rightarrow\)
      \(\text{max}_{\lambda_{i} \geq 0} U(\boldsymbol w, b, \lambda) = \begin{cases} \frac{1}{2}\| \boldsymbol w \|^{2} & \text{if constraints are satisfied as } \lambda_{i} \geq 0, g_{i} \geq 0 \\ + \infty & \text{O.W.} \end{cases}\)
      \(\rightarrow\)
      \(\text{min}_{\boldsymbol w, b} \text{max}_{\lambda_{i} \geq 0} U(\boldsymbol w, b, \lambda) = \frac{1}{2}\| \boldsymbol w \|^{2} - \sum_{i=1}^{N} \lambda_{i} (y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) - 1)\)
      where we maximize margin by selecting appropriate support vectors in \(\text{max}_{\lambda_{i} \geq 0}\)
      and we find optimal \(\boldsymbol w, b\) that minimizes \(U(\boldsymbol w, b, \lambda)\) in \(\text{min}_{\boldsymbol w, b}\)
      \(\rightarrow\)
      \(\nabla_{\boldsymbol w} U(\boldsymbol w, b, \lambda) = \boldsymbol w - \sum_{i=1}^{N} \lambda_{i} y_{i} x_{i} = 0\)
      So, \(\boldsymbol w = \sum_{i=1}^{N} \lambda_{i} y_{i} x_{i} \cdots (1)\)
      and
      \(\nabla_{b} U(\boldsymbol w, b, \lambda) = - \sum_{i=1}^{N} \lambda_{i} y_{i} = 0\)
      So, \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0 \cdots (2)\)
    • dual form :
      \((1), (2)\) 를 \(U(\boldsymbol w, b, \lambda)\) 에 대입해서 \(\boldsymbol w, b\) 를 소거하고 \(\lambda\) 만 남기면
      \(\text{max}_{\lambda_{i} \geq 0} \text{min}_{\boldsymbol w, b} U(\boldsymbol w, b, \lambda) = \text{max}_{\lambda_{i} \geq 0} U(\lambda) = \cdots = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} x_{i}^{T} x_{j}\)
      s.t. \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\)
      and \(\lambda_{i} \geq 0\)
      • training vectors의 inner product (\(x_{i}^{T} x_{j}\)) 꼴이므로 기존 primal form보다 much better!!
      • inner product 하니까 input space의 dimension과 cost function \(U(\boldsymbol w, b, \lambda)\) 는 무관
      • kernel의 inner product 형태로 non-linearly separable case에도 generalize 가능
      • optimal \(\lambda_{i}\) 를 구해서 얻은 optimal hyperplane (final result)는 unique하지만
        associated \(\lambda_{i}\) 와 이를 통해 구한 \(\boldsymbol w = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} x_{i}\) 의 uniqueness는 보장 못함
    • KKT condition :
      \(\lambda_{i} \geq 0\) (dual feasibility)
      and \(\lambda_{i} g_{i} = 0\) (complementary slackness)
      and \(g_{i} \geq 0\) (primal feasibility)
    • KKT condition 중 complementary slackness :
      \(\lambda_{i} g(x_{i}) = 0\) at optimality s.t. \(\lambda_{i} \geq 0\)
      • If \(\lambda_{i} \gt 0\), \(g(x_{i}) = 0\)
        즉, \(x_{i}\) 는 \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) = 1\) 을 만족하는 support vector
      • If \(g(x_{i}) \gt 0\), \(\lambda_{i} = 0\)
        즉, \(x_{i}\) 는 \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) \gt 1\) 을 만족하는 non-support vector
      • cannot happen \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) \lt 1\)
    • support vector만 \(\lambda_{i} \gt 0\) 이므로
      대부분의 samples는 \(\lambda_{i} = 0\) 라서 필요 없고
      support vector만 \(\boldsymbol w = \sum_{i=1}^{N} \lambda_{i} y_{i} x_{i} = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} x_{i}\) 에 영향을 줌
      where \(N_{s}\) : the number of support vectors

KKT condition 증명 및 primal form이 min-max of U와 같은 이유 증명

• Linear SVM Summary :
  • Step 1)
    primal form :
    \(\text{min}_{\boldsymbol w, b} U(\boldsymbol w, b, \lambda) = \frac{1}{2}\| \boldsymbol w \|^{2} - \sum_{i=1}^{N} \lambda_{i} (y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + b) - 1)\) for \(\lambda_{i} \geq 0\)
    이를 미분해서 얻은 \(\boldsymbol w = \sum_{i=1}^{N} \lambda_{i} y_{i} x_{i}\) 와 \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\) 를 대입하면
    dual form :
    \(\text{max}_{\lambda_{i} \geq 0} U(\lambda) = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} x_{i}^{T} x_{j}\) for \(\lambda_{i} \geq 0\) and \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\)
  • Step 2)
    quadratic programming으로 convex dual problem 풀어서 optimal \(\lambda_{i}\) 얻음
  • Step 3)
    optimal \(\lambda_{i}^{\ast}\) 과 complementary slackness \(\lambda_{i} g(x_{i}) = 0\) 이용해서
    optimal \(\boldsymbol w^{\ast}, b^{\ast}\) 얻음
    \(\boldsymbol w^{\ast} = \sum_{i=1}^{N_{s}} \lambda_{i}^{\ast} y_{i} x_{i}\)
    \(b^{\ast} = \frac{1}{y_{j}} - \sum_{i=1}^{N_{s}} \lambda_{i}^{\ast} y_{i} x_{i}^{T} x_{j} = \frac{1}{y_{j}} - \boldsymbol w^{\ast T} x_{j}\) (support vector \(x_{j}\) 1개 사용)
    또는
    \(b^{\ast} = \frac{1}{N_{s}} \sum_{j=1}^{N_{s}} (\frac{1}{y_{j}} - \sum_{i=1}^{N_{s}} \lambda_{i}^{\ast} y_{i} x_{i}^{T} x_{j}) = \frac{1}{N_{s}} \sum_{j=1}^{N_{s}} (\frac{1}{y_{j}} - \boldsymbol w^{\ast T} x_{j})\) (support vector \(x_{j}\) \(N_{s}\) 개 모두 사용하여 average value)

Cheet Sheet for Midterm Exam