EE534 Pattern Recognition Final

Lecture Summary (24F)

Lecture :
24F EE534 Pattern Recognition
by KAIST Munchurl Kim VICLab

Chapter 5. Linear Discriminant Functions

Linearly Non-Separable SVM

• new constraint :
  \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) \geq 1 - \xi_{i}\)
  \(\xi_{i}\) 를 도입하여 이제는 inside margin or misclassified 도 가능하지만 대신 \(C \sum_{i=1}^{N} \xi_{i}\) 를 loss에 넣어서 큰 \(\xi_{i}\) 값을 penalize
  • \(\xi = 0\) : outside margin or support vector
  • \(0 \lt \xi \leq 1\) : inside margin (correctly classified, but margin violation)
  • \(\xi \gt 1\) : misclassified

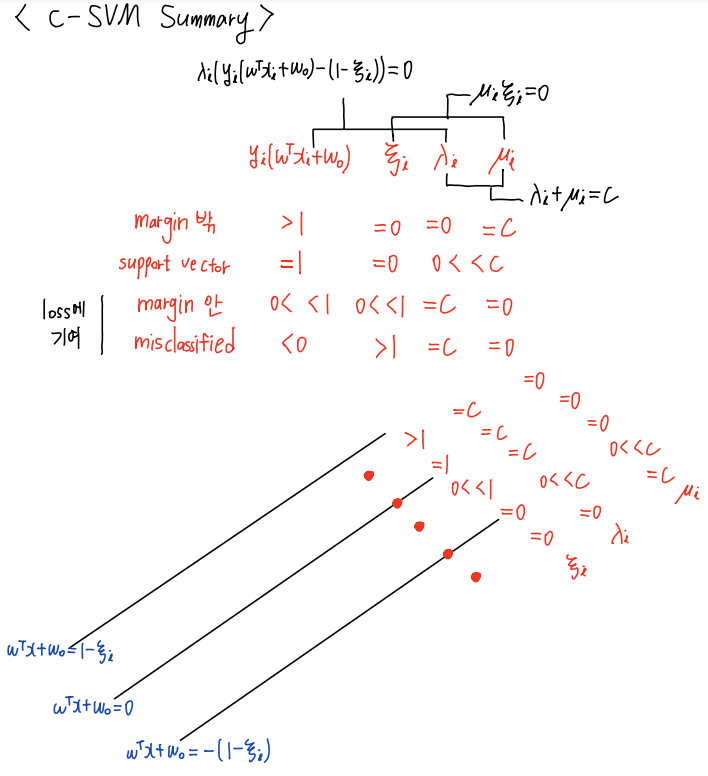
• 방법 1) 1-norm-soft-margin
  • constrained primal form :
    minimize \(J(\boldsymbol w, \xi) = \frac{1}{2} \| \boldsymbol w \|^{2} + C \sum_{i=1}^{N} \xi_{i}\)
    subject to \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) \geq 1 - \xi_{i}\) and \(\xi_{i} \geq 0\)
    • unconstrained primal form :
      이 때 위의 두 가지 constraints는 \(\xi_{i} = \text{max}(0, 1 - y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}))\) 로 하나로 합칠 수 있음
      따라서
      minimize \(J(\boldsymbol w, \xi) = \frac{1}{2} \| \boldsymbol w \|^{2} + C \sum_{i=1}^{N} \text{max}(0, 1 - y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}))\)
    • regularization param. \(C\) :
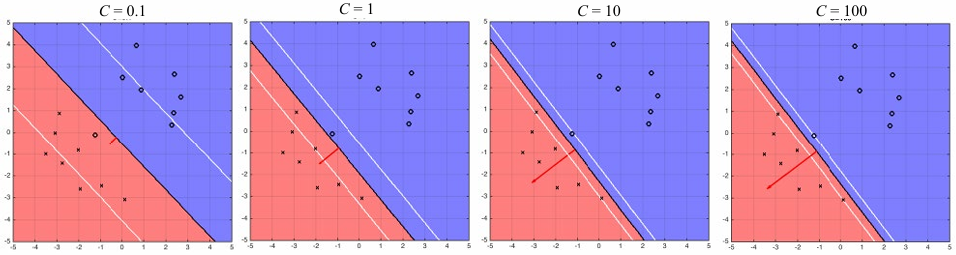
      • small \(C\) : 큰 \(\xi_{i}\) 값도 허용하므로 margin 커짐
      • large \(C\) : 큰 \(\xi_{i}\) 값은 허용 안 하므로 margin 작아짐
      • \(C = \infty\) : non-zero \(\xi_{i}\) 값 허용 안 하므로 hard margin (no sample inside margin)
        (Linearly Separable SVM 에 해당함)
  • Lagrangian :
    minimize \(L(\boldsymbol w, w_{0}, \xi, \boldsymbol \lambda, \boldsymbol \mu) = \frac{1}{2} \| \boldsymbol w \|^{2} + C \sum_{i=1}^{N} \xi_{i} - \sum_{i}^{N} \mu_{i} \xi_{i} - \sum_{i}^{N} \lambda_{i} (y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) - (1 - \xi_{i}))\)
    subject to \(\xi_{i}, \mu_{i}, \lambda_{i} \geq 0\)
    • \[\nabla_{\boldsymbol w} L = 0 \rightarrow \boldsymbol w = \sum_{i=1}^{N} \lambda_{i} y_{i} \boldsymbol x_{i}\]
    • \[\nabla_{w_{0}} L = 0 \rightarrow \sum_{i=1}^{N} \lambda_{i} y_{i} = 0\]
    • \[\nabla_{\xi_{i}} L = 0 \rightarrow C - \mu_{i} - \lambda_{i} = 0\]
  • KKT condition 중 slackness condition :
    • \[\lambda_{i} (y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) - (1 - \xi_{i})) = 0\]
    • \[\mu_{i} \xi_{i} = 0\]
  • dual form :
    위의 세 가지 식을 대입하여 \(\boldsymbol w, w_{0}, \xi_{i}, \mu_{i}\) 를 소거하면
    maximize \(L(\lambda) = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \boldsymbol x_{i}^{T} \boldsymbol x_{j}\)
    subject to \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\) and \(0 \leq \lambda_{i} \leq C\)
  • Summary :
    • Step 1) optimal \(\lambda_{i}^{\ast}\) 구하기
      \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\) and \(0 \leq \lambda_{i} \leq C\) 이용해서
      \(\nabla_{\lambda_{i}} L = 0\) 으로 아래의 dual form 풀어서
      (maximize \(L(\lambda) = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \boldsymbol x_{i}^{T} \boldsymbol x_{j}\))
      optimal \(\lambda_{i}\) 얻음
    • Step 2) optimal \(\boldsymbol w^{\ast}, w_{0}^{\ast}\) 구하기
      • \(\boldsymbol w^{\ast} = \sum_{i=1}^{N_{s}} \lambda_{i}^{\ast} y_{i} x_{i}\)
        (\(N_{s}\) : support vector 개수)
        (hyperplane 결정할 때는 \(\lambda_{i} \gt 0\) 중에 \(\xi = 0\) 인 support vectors만 고려!!)
      • \(w_{0}^{\ast} = \frac{1}{y_{j}} - \sum_{i=1}^{N_{s}} \lambda_{i}^{\ast} y_{i} x_{i}^{T} x_{j} = \frac{1}{y_{j}} - \boldsymbol w^{\ast T} x_{j}\)
        (support vector \(x_{j}\) 1개 사용)
        또는
        \(w_{0}^{\ast} = \frac{1}{N_{s}} \sum_{j=1}^{N_{s}} (\frac{1}{y_{j}} - \sum_{i=1}^{N_{s}} \lambda_{i}^{\ast} y_{i} x_{i}^{T} x_{j}) = \frac{1}{N_{s}} \sum_{j=1}^{N_{s}} (\frac{1}{y_{j}} - \boldsymbol w^{\ast T} x_{j})\)
        (support vector \(x_{j}\) \(N_{s}\)-개 모두 사용하여 average value)
    • Tip : hard margin (no sample inside margin) 의 경우
      육안으로 어떤 sample이 support vector일지 판단 가능하다면
      complementary slackness condition (\(\lambda_{i} (y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) - (1 - \xi_{i})) = 0\)) 에서
      support vector만 \(\lambda_{i} \gt 0\) 이므로
      연립해서 \(\boldsymbol w^{\ast}, w_{0}^{\ast}\) 바로 구할 수 있음

• 방법 2) 2-norm-soft-margin
  • 차이점 1) primal form
    minimize \(J(\boldsymbol w, \xi) = \frac{1}{2} \| \boldsymbol w \|^{2} + C \sum_{i=1}^{N} \xi_{i}\)
    subject to \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) \geq 1 - \xi_{i}\) and \(\xi_{i} \geq 0\)
    대신
    minimize \(J(\boldsymbol w, \xi) = \frac{1}{2} \| \boldsymbol w \|^{2} + \frac{1}{2} C \sum_{i=1}^{N} \xi_{i}^{2}\)
    subject to \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) \geq 1 - \xi_{i}\) and \(\xi_{i} \geq 0\)
  • 차이점 2) Lagrangian
    \(\nabla_{\xi_{i}} L(\boldsymbol w, w_{0}, \boldsymbol \xi, \boldsymbol \lambda, \boldsymbol \mu) = 0\) 했을 때
    \(C - \mu_{i} - \lambda_{i} = 0\)
    대신
    \(C \xi_{i} - \mu_{i} - \lambda_{i} = 0\)
  • 차이점 3) dual form
    maximize \(L(\lambda) = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \boldsymbol x_{i}^{T} \boldsymbol x_{j}\)
    subject to \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\) and \(0 \leq \lambda_{i} \leq C\)
    대신
    maximize \(L(\lambda) = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \boldsymbol x_{i}^{T} \boldsymbol x_{j} - \frac{1}{2C} \sum_{i=1}^{N} (\lambda_{i} + \mu_{i})^{2}\)
    subject to \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\) and \(0 \leq \lambda_{i} \leq C\)
• Remark :
  • Linearly Non-Separable SVM에서
    \(C \rightarrow \infty\) 하면 Linearly Separable SVM
    e.g. non-linear에서는 \(0 \leq \lambda_{i} \leq C\) 인데, linear에서는 \(0 \leq \lambda_{i} \lt \infty\)
  • SVM의 한계 :
    high computational complexity
    (SVM training은 주로 batch mode로 진행되어 memory를 많이 필요로 하므로
    training dataset을 subset으로 나눠서 training 진행)
  • 지금까지는 SVM for two-category만 살펴봤는데,
    M-class 의 경우 M개의 discriminant function \(g_{i}(x)\) 를 design하여
    assign \(x\) to class \(w_{i}\) if \(i = \text{argmax}_{k} g_{k}(x)\)

v-SVM

• v-SVM :
  • hyperplane
    \(\boldsymbol w^{T} \boldsymbol x_{i} + w_{0} = \pm 1\)
    대신
    \(\boldsymbol w^{T} \boldsymbol x_{i} + w_{0} = \pm \rho\)
    where \(\rho \geq 0\) : var. to be optimized
  • margin
    margin은 \(\frac{2 \rho}{\| w \|}\) 이므로
    margin을 maximize하려면
    \(\| w \|\) minimize 뿐만 아니라 \(\rho\) maximize하면 되므로
    둘 다 primal form loss term에 넣음
  • primal form
    minimize \(J(\boldsymbol w, \xi, \rho) = \frac{1}{2} \| \boldsymbol w \|^{2} - v \rho + \frac{1}{N} \sum_{i=1}^{N} \xi_{i}\)
    subject to \(y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) \geq \rho - \xi_{i}\) and \(\xi_{i} \geq 0\) and \(\rho \geq 0\)
  • Lagrangian
    \(L(\boldsymbol w, w_{0}, \boldsymbol \xi, \rho, \boldsymbol \lambda, \boldsymbol \mu, \delta) = \frac{1}{2} \| \boldsymbol w \|^{2} - v \rho + \frac{1}{N} \sum_{i=1}^{N} \xi_{i} - \sum_{i}^{N} \mu_{i} \xi_{i} - \sum_{i}^{N} \lambda_{i} (y_{i} (\boldsymbol w^{T} \boldsymbol x_{i} + w_{0}) - (\rho - \xi_{i})) - \delta \rho\)
    • \(\nabla_{\boldsymbol w} L = 0\) 했을 때
      \(\boldsymbol w = \sum_{i=1}^{N} \lambda_{i} y_{i} \boldsymbol x_{i}\)
    • \(\nabla_{w_{0}} L = 0\) 했을 때
      \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\)
    • \(\nabla_{\xi_{i}} L = 0\) 했을 때
      \(\mu_{i} + \lambda_{i} = \frac{1}{N}\)
    • \(\nabla_{\rho} L = 0\) 했을 때
      \(\sum_{i=1}^{N} \lambda_{i} - \delta = v\)
  • KKT condition 중 complementary slackness
    For \(\lambda_{i} \geq 0\) and \(\mu_{i} \geq 0\) and \(\delta \geq 0\),
    • \[\lambda_{i} (y_{i}(\boldsymbol w^{T} \boldsymbol x + w_{0}) - (\rho - \xi_{i})) = 0\]
    • \[\mu_{i} \xi_{i} = 0\]
    • \[\delta \rho = 0\]
  • dual form
    maximize \(L(\lambda) = - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \boldsymbol x_{i}^{T} \boldsymbol x_{j}\)
    subject to \(\sum_{i=1}^{N} \lambda_{i} y_{i} = 0\) and \(0 \leq \lambda_{i} \leq \frac{1}{N}\) and \(\sum_{i=1}^{N} \lambda_{i} = \delta + v \geq v\)
    • \(\lambda\) 만 explicitly 남아 있고,
      margin var. \(\rho\) 와 slack var. \(\xi_{i}\) 는 constraint의 bounds에 implicitly 들어 있음
    • v-SVM에서는 \(\sum_{i=1}^{N} \lambda_{i}\) term이 없으므로
      optimal \(\lambda_{i}\) 는 quadratically homogeneous solution
    • 새로운 constraint \(\sum_{i=1}^{N} \lambda_{i} \geq v\) 있음

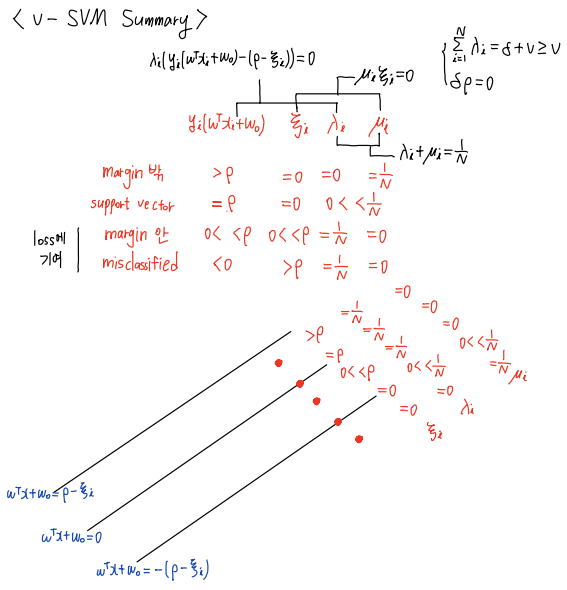
• Remark
  • v-SVM의 경우 \(0 \leq v \leq 1\) 이어야 optimizable
  • C-SVM에 비해 v-SVM은
    error rate와 support vector 수 bound 측면에서 장점 ???
  • \(\rho \gt 0\) 일 때 \(\delta = 0\) 이므로
    \(\sum_{i=1}^{N} \lambda_{i} = v\)
  • loss (error)에 기여하는 애들은
    \(\xi_{i} \gt 0\), 즉 \(\mu_{i} = 0\), 즉 \(\lambda_{i} = \frac{1}{N}\) 이다
    따라서 error rate = \(\sum_{i=1}^{N_{error}} \lambda_{i} = \frac{N_{error}}{N} \leq \sum_{i=1}^{N} \lambda_{i} = v\)
    즉, error rate \(\frac{N_{error}}{N} \leq v\) 이고
    total number errors \(N_{error} \leq N v\)
  • Since \(0 \lt \lambda_{i} \lt 1\) for support vector \(i\),
    \(v = \sum_{i=1}^{N} \lambda_{i} = \sum_{i=1}^{N_{s}} \lambda_{i} \leq \sum_{i=1}^{N_{s}} \frac{1}{N} = \frac{N_{s}}{N}\)
    즉, \(vN \leq N_{s}\)
    (\(\lambda_{i} \gt 0\) 중에 \(\xi = 0\) 인 support vectors만 고려하면 \(\sum_{i=1}^{N} \lambda_{i} = \sum_{i=1}^{N_{s}}\) !!)
  • \(\frac{N_{error}}{N} \leq v \leq \frac{N_{s}}{N}\) 이므로
    \(v\) optimize하면 error rate와 support vector 개수도 bound 알 수 있음
  • support vector 수 \(N_{s}\) 는 classifier performance에 있어서 매우 중요
    (\(N_{s}\) 가 클수록 inner product 많이 계산해야 돼서 computational cost 높아짐)
    (\(N_{s}\) 가 크면 training set 이외의 data에 대한 performance가 제한되어 poor generalization)

Kernel Method for SVM

• discriminant function :
  \(x\) 의 inner product 꼴
  \(g(\boldsymbol x) = \boldsymbol w^{T} \boldsymbol x + w_{0} = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} \boldsymbol x_{i}^{T} \boldsymbol x + w_{0}\)

• Cover’s theorem :
  non-linearly separable D-dim. space는
  linearly separable space of high enough dim. 으로 transform 될 수 있다
  (separating hyperplane의 optimality는 관심사 아님)

• Kernel Method for SVM :
  discriminant function \(g(\boldsymbol x) = \boldsymbol w^{T} \boldsymbol x + w_{0} = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} \boldsymbol x_{i}^{T} \boldsymbol x + w_{0}\) 에서
  kernel \(K(\boldsymbol x_{i}, \boldsymbol x) = \boldsymbol x_{i}^{T} \boldsymbol x\)
  (inner product b.w. support vector and input vector)
  대신
  다른 kernel \(K(\boldsymbol x_{i}, \boldsymbol x) = \Phi(\boldsymbol x_{i})^{T} \Phi(\boldsymbol x)\) 을 써서
  non-linearly separable samples도 분류해보자!

  • Step 1)
    input vector \(\boldsymbol x\) 와 training samples \(\boldsymbol x_{i}\) 를 high-dim.으로 project by function \(\Phi(\cdot)\)
  • Step 2)
    transformed vector \(\Phi (\boldsymbol x)\) 와 \(\Phi (\boldsymbol x_{i})\) 에 대해 linear SVM 적용
    \(g(\boldsymbol x) = \boldsymbol w^{T} \Phi (\boldsymbol x) + w_{0}\)

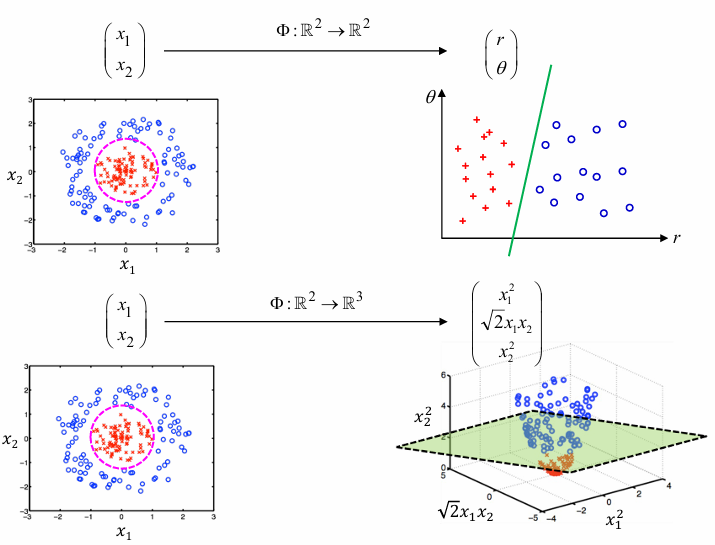
• Kernel Trick :
  \(\boldsymbol x_{i}^{T} \boldsymbol x_{j}\) 대신 \(K(\boldsymbol x_{i}, \boldsymbol x_{j}) = \Phi(\boldsymbol x_{i})^{T} \Phi(\boldsymbol x_{j})\) 쓰면 됨!!
  • optimization of dual form :
    maximize \(L(\lambda) = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} \boldsymbol x_{i}^{T} \boldsymbol x_{j}\)
    대신
    maximize \(L(\lambda) = \sum_{i=1}^{N} \lambda_{i} - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_{i} \lambda_{j} y_{i} y_{j} K(\boldsymbol x_{i}, \boldsymbol x_{j})\)
    where \($K(\boldsymbol x_{i}, \boldsymbol x_{j}) = \Phi(\boldsymbol x_{i})^{T} \Phi(\boldsymbol x_{j})\)
  • hyperplane :
    \(g(\boldsymbol x) = \boldsymbol w^{T} \boldsymbol x + w_{0} = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} \boldsymbol x_{i}^{T} \boldsymbol x + w_{0} = 0\)
    대신
    \(g(\boldsymbol x) = \boldsymbol w^{T} \Phi(\boldsymbol x) + w_{0} = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} \Phi(\boldsymbol x_{i})^{T} \Phi(\boldsymbol x) + w_{0} = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} K(\boldsymbol x_{i}, \boldsymbol x) + w_{0} = 0\)
    where \(\boldsymbol w = \sum_{i=1}^{N_{s}} \lambda_{i} y_{i} \Phi(\boldsymbol x_{i})\)
• Remark :
  • polynomial learning machine, radial-basis function network, two-layer perceptron(single hidden layer) 와 같은
    kernel-based learning machine을 만들 때
    support vector learning algorithm을 사용
    • polynomial :
      \(K(x, z) = (x^{T} z + 1)^{q}\) for \(q \gt 0\)
    • radial-basis function :
      \(K(x, z) = \text{exp}(-\frac{\| x - z \|^{2}}{\sigma^{2}})\)
    • hyperbolic tangent :
      \(K(x, z) = \text{tanh}(\beta x^{T} z + \gamma)\) where typical value is \(\beta = 2\) and \(\gamma = 1\)
• 문제 풀이 예시 :

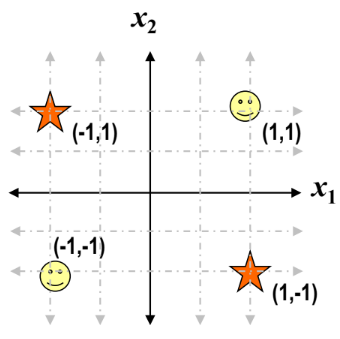
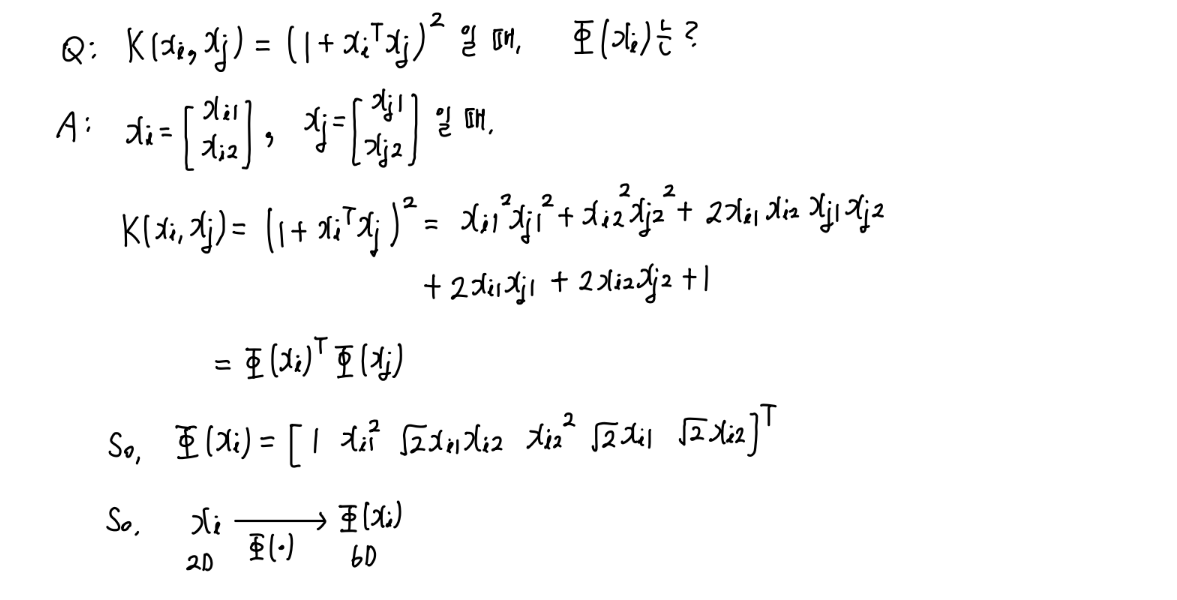
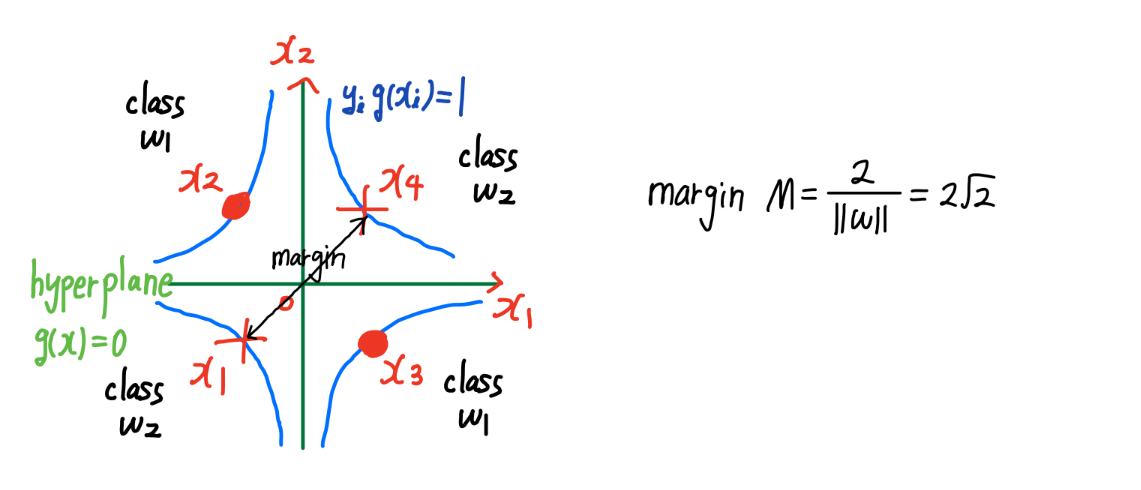
Chapter 6. Multilayer Neural Networks

• activation function :
  • unipolar sigmoid :
    \(\phi (x) = \frac{1}{1 + exp(-x)}\)
    \(\phi^{'} (x) = \phi (x) (1 - \phi (x))\)
  • bipolar sigmoid (tanh) :
    \(\phi (x) = \text{tanh} (x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\)
    \(\phi^{'} (x) = 1 - \text{tanh}^{2} (x) = 1 - \phi^{2} (x)\)
    • tanh가 sigmoid보다 gradient 더 커서 같은 \(\eta\) 일 때 학습 더 많이 함
  • ReLU
• weight initialization :
  • zero-mean uniform distribution \(U(0, \sigma^{2})\)
    where \(\sigma^{2}\) is chosen so that std of induced local fields of neurons lie in the linear transition interval of sigmoid activation function
• weight update :
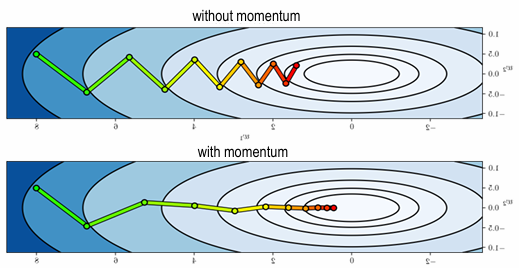
  \(w_{ji}(n+1) = w_{ji}(n) + \eta \delta_{j} (n) y_{i} (n) + \alpha (w_{ji} (n) - w_{ji} (n-1))\)
  where \(\eta\) : learning rate
  where \(\alpha\) : momentum constant
  (momentum in back-prop has stabilizing effect when gradient has oscillate in sign)

Back-propagation Algorithm

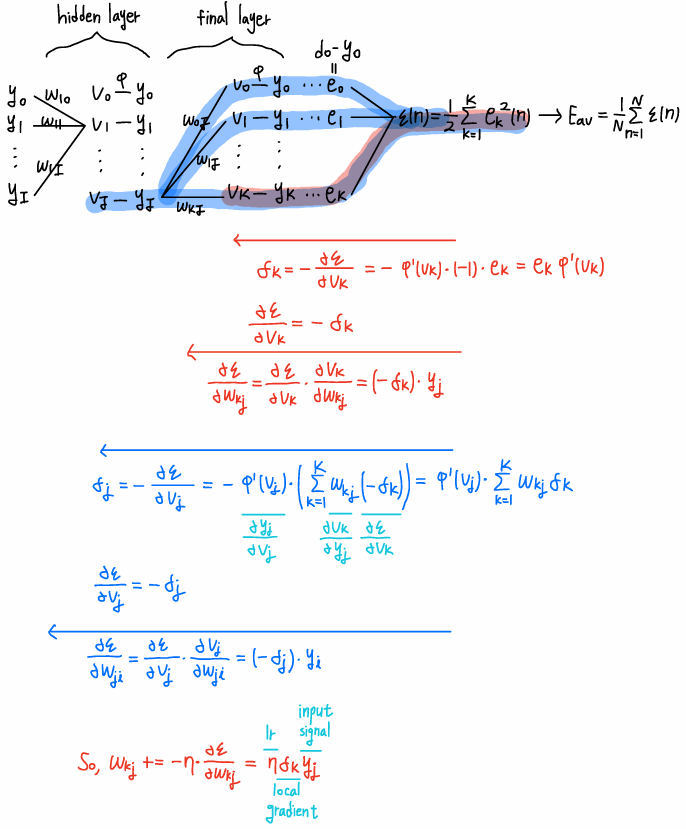
Issues on Neural Networks

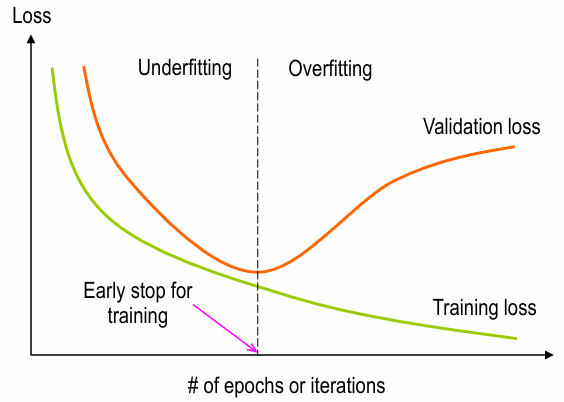
• Stopping criteria :
  • Euclidean norm of gradient reaches sufficiently small threshold
  • absolute rate of change in average squared error per epoch is sufficiently small
  • generalization performance (tested after each iter.) has peaked
• Weight Update :
  • sample-by-sample mode :
    weights are updated after presenting each training sample
    \(w_{ji}(n+1) = w_{ji}(n) + \eta \delta_{j} (n) y_{i} (n) + \alpha (w_{ji} (n) - w_{ji} (n-1))\)
    • very sensitive to each sample so that the weight update term is very noisy
  • batch mode :
    weights are updated after presenting entire set of training samples
    \(w_{ji}(t+1) = w_{ji}(t) + \eta \frac{1}{N} \sum_{n=1}^{N} \delta_{j} (n) y_{i} (n) + \alpha (w_{ji} (t) - w_{ji} (t-1))\)
• k-fold cross validation :

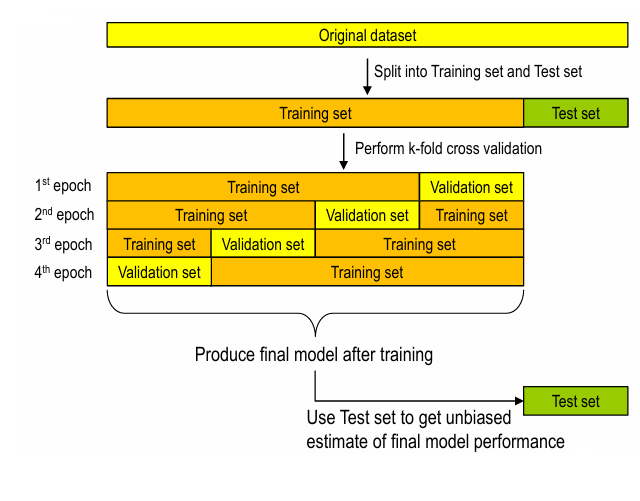
• Normalization : Whitening
  • mean removal
  • de-correlation
  • scaling for equal covariance
    (then input var. in training set becomes uncorrelated)
    (then gradient descent converges faster)

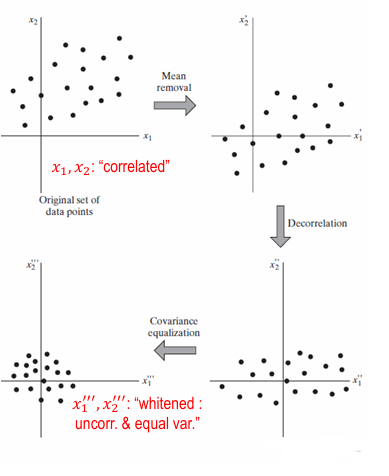
• Gradient Vanish 해결 방법 :
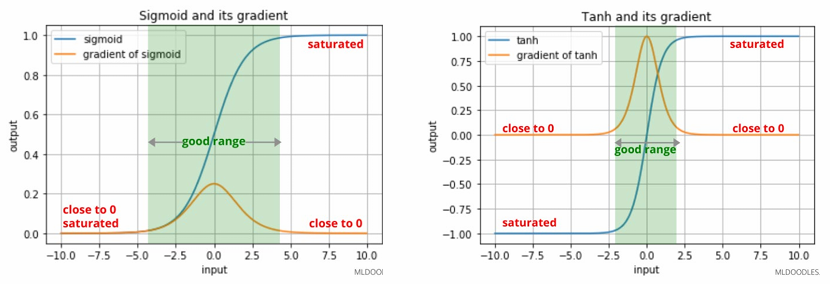
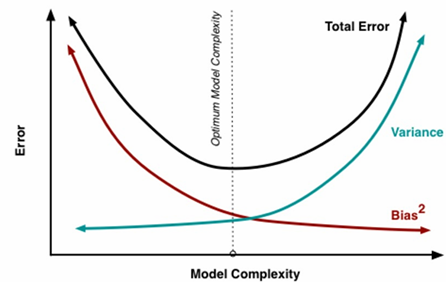
  • 방법 1) Batch Normalization
    Batch Normalization을 해서 input이 \(0\) 주위의 가파른 부분에 머무르도록 함
    근데 sigmoid의 경우 gradient가 [0, 0.25] 이고, tanh의 경우 gradient가 [0, 1] 이므로
    여전히 gradient vanishing 문제 발생
  • 방법 2) ReLU activation
    ReLU의 gradient는 0 또는 1이므로
    gradient value 1의 경우 gradient vanishing 문제 없음
  • 방법 3) Residual Network
    skip connection 사용하여
    non-linear activation 통과하지 않고 바로 gradient가 흘러들어갈 수 있도록 함

• Bias-Variance dilemma :
  • prediction error의 종류로는 bias, variance, irreducible error가 있음
    MSE \(E_{x, y, D}[\epsilon^{2} (x)] = E_{x, y, D}[(h_{D}(x) - y)^{2}]\)
    \(= E_{x, D}[(h_{D}(x) - \bar h(x))^{2}] + E_{x}[(\bar h(x) - \bar y(x))^{2}] + E_{x, y}[(\bar y(x) - y)^{2}]\)
    • variance of model : \(E_{x, D}[(h_{D}(x) - \bar h(x))^{2}]\)
      where \(h_{D}(x)\) : model output
      where \(\bar h(x)\) : model mean
      • different test dataset으로 테스트했을 때 변하는 정도
      • particular training dataset에 overfitting된 정도
    • bias of model : \(\bar h(x) - \bar y(x)\)
      where \(\bar y(x)\) : label mean
      • data를 아무리 많이 학습시켜도 model 특성 때문에 발생하는 inherent error
        e.g. linear classifier is biased to a particular kind of solution
    • data noise : \(E_{x, y}[(\bar y(x) - y)^{2}]\)
      • ambiguity due to data distribution and feature representation
  • trade-off :
    • too simple model : high bias
      \(\rightarrow\) 해결법 : pick more complex model
    • too complex model : high variance
      \(\rightarrow\) naive 해결법 : use more data, but it requires high cost

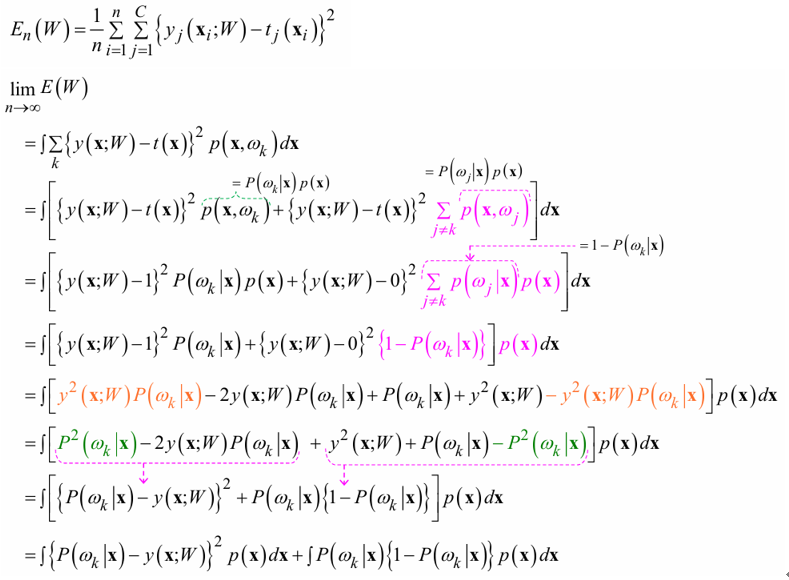
• SSE (Sum of Squared Errors) :
  위의 유도 결과에서
  두 번째 term은 model weight와 무관하므로
  back-propagation은 첫 번째 term만 minimize
  즉, \(y_{k}(x; W) \approx P(w_{k} | x)\)
  이 때, 잘 approx.하려면 model이 충분한 layers, neurons를 가지고 있어야 함
  • \(y_{k}(x; W)\) : model output

  • $$P(w_{k}

    x)$$ : true posteriori probability (Bayes linear discriminant function)

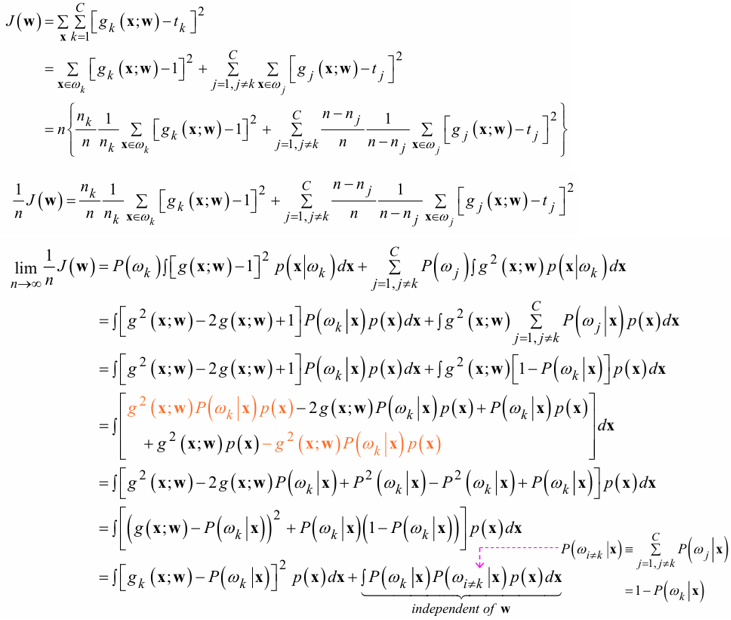
Chapter 7. Stochastic Methods for Pattern Classification

• Learning :
  • deterministic learning :
    무조건 loss 작아지는 방향으로 이동
    e.g. gradient descent
  • stochastic learning :
    작은 확률이겠지만 energy 커지는 방향으로 이동하는 것도 허용
    \(\rightarrow\) local minima에 빠지는 문제 해결하여 global minimum에 도달 가능 e.g. Simulated Annealing, Boltzmann Machine
• Boltzmann Machine :
  • neuron :
    • visible neuron : \(\alpha = \{ \alpha^{i}, \alpha^{o} \}\)
    • hidden neuron : \(\beta\)
  • probability \(P(\alpha) = \sum_{\beta} P(\alpha \beta) = \sum_{\beta} \frac{e^{- E_{\alpha \beta} / T}}{Z} = \sum_{\beta} \frac{e^{- E_{\alpha \beta} / T}}{\sum_{\alpha \beta} e^{- E_{\alpha \beta} / T}}\)
    where energy \(E_{\gamma} = - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} w_{ij} s_{i} s_{j}\)
    where \(w_{ij} = w_{ji}\) is symmetric with \(w_{ii} = 0\)
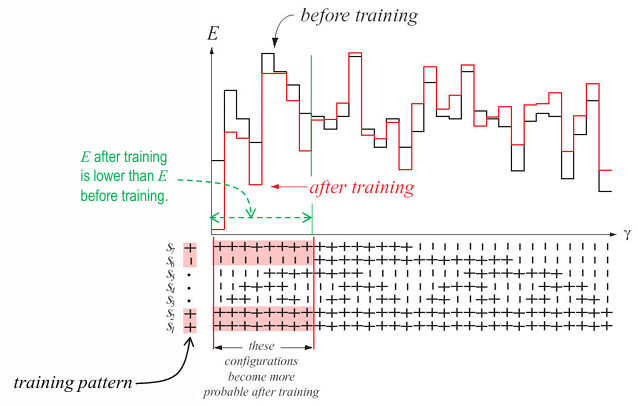
    즉, energy \(E_{\gamma}\) 가 낮을수록 configuration \(\alpha\) 일 확률 \(P(\alpha)\) 가 높음
  • goal :
    \(P(\alpha)\) 가 \(Q(\alpha)\) 와 최대한 가까워지도록
    weight \(w_{ij}\) 를 학습
    • marginal (estimated) distribution of generated samples \(P(\alpha)\) :
      network가 free-running일 때 (all neurons가 자유롭게 업데이트될 수 있을 때)
      visible neuron이 \(\alpha\) 일 확률
    • observed (desired) distribution of training samples \(Q(\alpha)\) :
      network의 visible neuron이 \(\alpha\) 로 clamped되었을 때
      visible neuron이 \(\alpha\) 일 확률
    • KL-divergence \(D_{KL} (Q(\alpha), P(\alpha)) = \sum_{\alpha} Q(\alpha) \text{log} \frac{Q(\alpha)}{P(\alpha)}\) 를 minimize하면
      \(\Delta w_{ij} = - \eta \frac{\partial D_{KL}}{\partial w_{ij}} = \eta \sum_{\alpha} \frac{Q(\alpha)}{P(\alpha)} \frac{\partial P(\alpha)}{\partial w_{ij}} = \frac{\eta}{2T}(\sum_{\alpha \beta} Q(\alpha) P(\beta | \alpha) s_{i} s_{j} - \sum_{\alpha^{'} \beta^{'}} P(\alpha^{'} \beta^{'}) s_{i} s_{j}) = \frac{\eta}{2T}(E_{Q}[s_{i} s_{j}]_{\text{clamped by} \alpha} - E[s_{i} s_{j}]_{\text{free}})\)
      (pf는 아래에)

• Boltzmann Machine with I-O Association :
  • neuron :
    • visible neuron :
      • input neuron : \(\alpha\)
      • output neuron : \(\gamma\)
    • hidden neuron : \(\beta\)
  • goal :
    \(P(\gamma | \alpha)\) 가 \(Q(\gamma | \alpha)\) 와 최대한 가까워지도록
    weight \(w_{ij}\) 를 학습
    • KL-divergence \(D_{KL} (Q(\gamma | \alpha), P(\gamma | \alpha)) = D_{KL} (Q(\alpha \gamma), P(\alpha \gamma)) - D_{KL} (Q(\alpha), P(\alpha))\) 를 minimize하면
      \(\Delta w_{ij} = \frac{\eta}{2T}(E_{Q}[s_{i} s_{j}]_{\text{clamped by} \alpha \gamma} - E[s_{i} s_{j}]_{\text{clamped by} \alpha})\)
      (pf는 아래에)

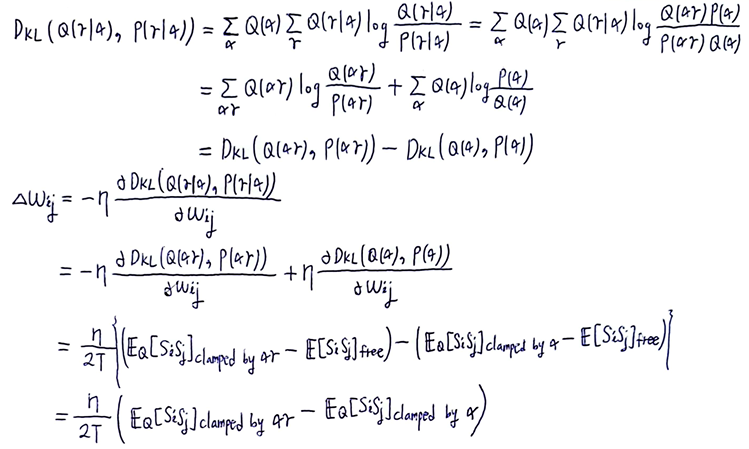
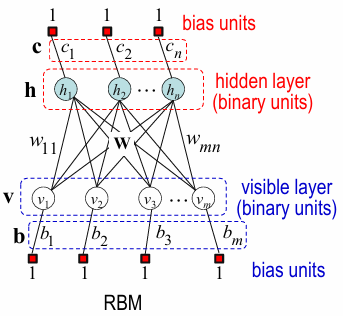
• Restricted Boltzmann Machine (RBM) :
  Boltzmann Machine with bi-partite graph of visible and hidden units
  • probability \(P(v) = \sum_{h} P(v, h) = \sum_{h} \frac{e^{- E(v, h)}}{Z}\)
    where (intractable) partition function \(Z = \sum_{v, h} e^{- E(v, h)}\)
    where energy \(E(v, h) = - h^{T} W v - b^{T} v - c^{T} h\) for \(T=1\)
  • goal :
    training dataset의 distribution을 학습!!
    • 훈련 끝나고나면 해당 distribution을 따르는 new sample을 generate할 수 있음!! image inpainting에도 적용 가능
    • label과의 joint distribution을 학습하여 classification 수행 가능!! feed-forward layer를 initialize할 때 RBM weight 사용 가능
    • feature extractor 역할 수행 가능!!
• Training RBM 수식 유도 :
  • weight \(\theta = [W, b, c]\) 에 대해
    \(\hat \theta = \text{argmax}_{\theta} \text{ln} P(v | \theta) = \text{argmax}_{\theta} \text{ln} \sum_{h} \frac{e^{- E(v, h | \theta)}}{Z} = \text{argmax}_{\theta} \text{ln} \sum_{h} e^{- E(v, h | \theta)} - \text{ln} Z\)
    \(\rightarrow\)
    \(\frac{\partial - \text{ln} P(v | \theta)}{\partial \theta} = \cdots = \sum_{h} P(h | v, \theta) \frac{\partial E(v, h | \theta)}{\partial \theta} - \sum_{v, h} P(v, h | \theta) \frac{\partial E(v, h | \theta)}{\partial \theta} = E_{h \sim P(h | v, \theta)}[\frac{\partial E(v, h | \theta)}{\partial \theta}] - E_{(v, h) \sim P(v, h | \theta)}[\frac{\partial E(v, h | \theta)}{\partial \theta}]\)
    • 오른쪽 expectation 식 :
      model distribution \(P(v, h | \theta)\) 의 모든 경우의 수에 대해 expectation \(E[\cdot]\) 계산하려면 \(2^{m+n}\) 로 costly하므로
      MCMC (Markov chain Monte Carlo) 기법으로 해당 distribution에서 Gibbs sampling 수행하여
      오른쪽 expectation 식을 sample mean으로 approx.
  • RBM의 경우 visible units끼리, hidden units끼리는 connection 없으므로
    given visible units에 대해 hidden units끼리는 conditionally independent하므로
    같은 layer에 있는 units는 쉽게 jointly(동시에) Gibbs sampling 가능
    \(\rightarrow\)
    Gibbs sampling은 두 단계로 요약 가능 (block Gibbs sampling)
    • Step 1)
      sample \(h\) based on \(P(h | v)\)
    • Step 2)
      sample \(v\) based on \(P(v | h)\)
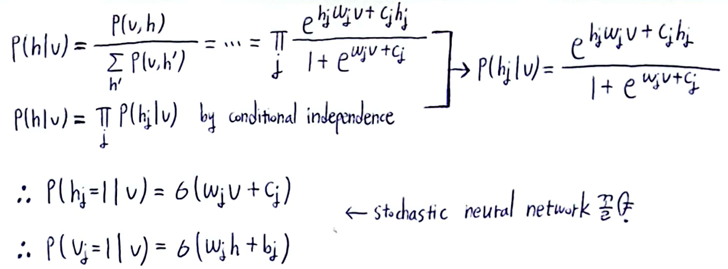
  • Conditional Distribution :
    proof는 아래 아래 사진에
    • \[P(h_{i} = 1 | v) = \sigma (\sum_{j=1}^{m} w_{ij} v_{j} + c_{i}) = \sigma (\boldsymbol w_{i} \cdot \boldsymbol v + c_{i})\]
    • \[P(v_{j} = 1 | h) = \sigma (\sum_{i=1}^{n} w_{ij} h_{i} + b_{j}) = \sigma (\boldsymbol w_{j} \cdot \boldsymbol h + b_{j})\]

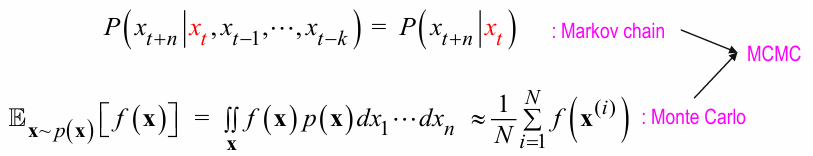
• Training RBM 수식 유도 (continued) :
  • goal :
    \(P(v | \theta)\) 가 \(Q(v)\) 와 최대한 가까워지도록
    weight \(W, b, c\) 를 학습
    • Gradient of Log-Likelihood :
      (proof는 아래 사진에)
      Let’s define
      \(\boldsymbol h (\boldsymbol v_{0}) = P(\boldsymbol h = \boldsymbol 1 | \boldsymbol v_{0}, \theta) = \sigma(\boldsymbol W \boldsymbol v_{0} + \boldsymbol b)\)
      \(\boldsymbol v_{0} \in S\) : clamped training sample where \(S\) is training dataset
      \(\boldsymbol v_{k}\) : generated sample by RBM
      KL-divergence \(D_{KL} (Q(v), P(v | \theta)) = \sum_{v} Q(v) \text{log} \frac{Q(v)}{P(v | \theta)}\) 를 minimize하려면
      • \[\Delta W \propto \frac{1}{N} \sum_{\boldsymbol v_{0} \in S} \boldsymbol h (\boldsymbol v_{0}) \boldsymbol v_{0}^{T} - \boldsymbol h (\boldsymbol v_{k}) \boldsymbol v_{k}^{T}\]
      • \[\Delta b \propto \frac{1}{N} \sum_{\boldsymbol v_{0} \in S} \boldsymbol v_{0}^{T} - \boldsymbol v_{k}^{T}\]
      • \[\Delta c \propto \frac{1}{N} \sum_{\boldsymbol v_{0} \in S} \boldsymbol h (\boldsymbol v_{0}) - \boldsymbol h (\boldsymbol v_{k})\]

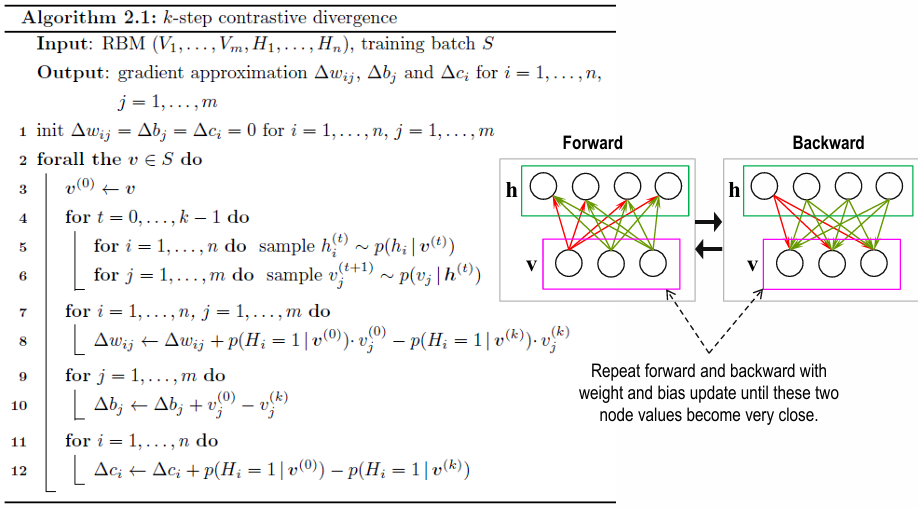
• k-step Contrastive Divergence :
  model expectation은 exponential cost 가지므로
  sampling from RBM distribution
  대신
  k-step sampling from Gibbs chain initialized with training data
  Then, \(\frac{\partial - \text{ln} P(v | \theta)}{\partial \theta} \approx \sum_{h} P(h | v_{0}) \frac{\partial E(v_{0}, h)}{\partial \theta} - \sum_{h} P(h | v_{k}) \frac{\partial E(v_{k}, h)}{\partial \theta}\)

• Training RBM Summary :
  • Step 1) Positive Phase
    training sample \(\boldsymbol v_{0}\) 에서 시작하여
    sample \(h_{i}\) from \(Q(h_{i} = 1 | v_{j}) = \sigma (\boldsymbol w_{i} \cdot \boldsymbol v + c_{i})\)
    \(\rightarrow\)
    \(h_{i} = \begin{cases} 1 & \text{if} & \text{rand}(0, 1) \lt Q(h_{i}=1 | v_{j}) \\ 0 & \text{O.W.} & \text{} \end{cases}\)
  • Step 2) Negative Phase (Recon. Phase)
    sample \(v_{j}\) from \(P(v_{j} = 1 | h_{i}) = \sigma (\boldsymbol w_{j} \cdot \boldsymbol h + b_{j})\)
    \(\rightarrow\)
    \(v_{j} = \begin{cases} 1 & \text{if} & \text{rand}(0, 1) \lt P(v_{j}=1 | h_{i}) \\ 0 & \text{O.W.} & \text{} \end{cases}\)
  • Step 3) 위의 과정을 k-step 반복
    \(\boldsymbol v_{0}\) 으로부터 \(\boldsymbol h(\boldsymbol v_{0})\) 얻고
    \(\cdots\) (Gibbs sampling k-step 반복) \(\cdots\)
    \(\boldsymbol v_{k}\) 으로부터 \(\boldsymbol h(\boldsymbol v_{k})\) 얻음
  • Step 4) Update Weights
    • \[\Delta W \propto \frac{1}{N} \sum_{\boldsymbol v_{0} \in S} \boldsymbol h (\boldsymbol v_{0}) \boldsymbol v_{0}^{T} - \boldsymbol h (\boldsymbol v_{k}) \boldsymbol v_{k}^{T}\]
    • \[\Delta b \propto \frac{1}{N} \sum_{\boldsymbol v_{0} \in S} \boldsymbol v_{0}^{T} - \boldsymbol v_{k}^{T}\]
    • \[\Delta c \propto \frac{1}{N} \sum_{\boldsymbol v_{0} \in S} \boldsymbol h (\boldsymbol v_{0}) - \boldsymbol h (\boldsymbol v_{k})\]
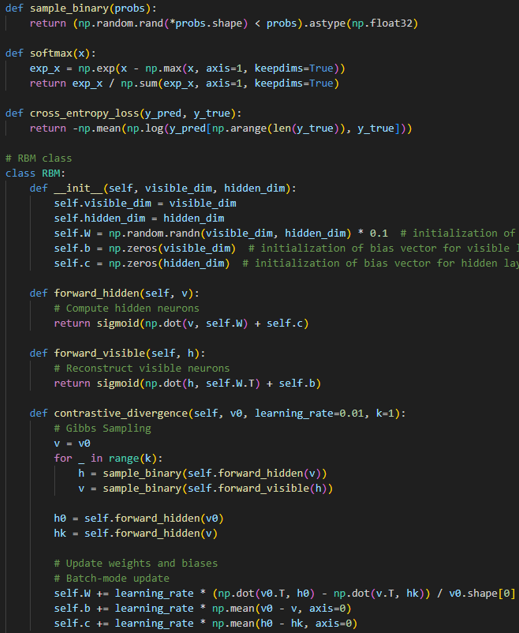
• RBM Code :

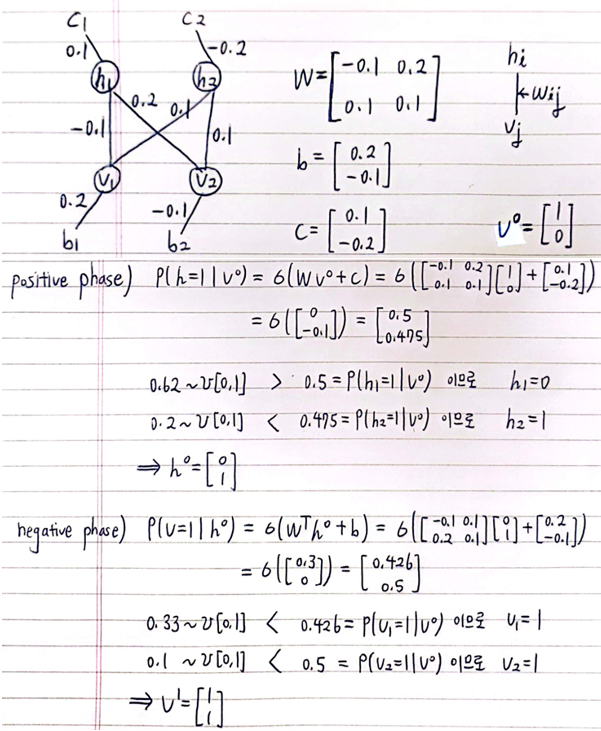
• Example :

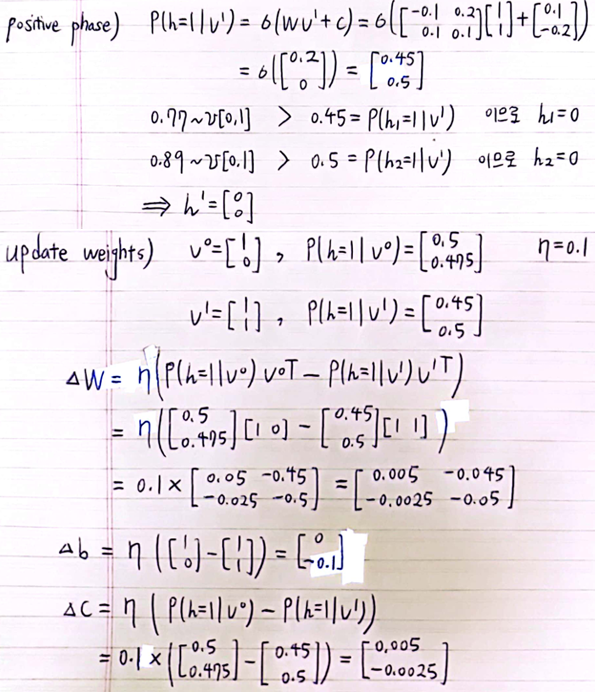
Chapter 8. Non-metric Methods for Pattern Classification

training data 전체에 부합하는 parametric boundary 찾는 대신
feature space를 여러 tree level에서 sub-regions로 나눠서 classify independently

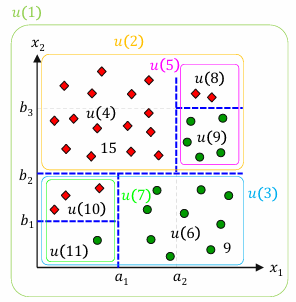
• Decision Tree :
  not unique for partition
  • probability that \(\boldsymbol x \in u(t)\) has class \(w_{j}\) :
    \(N(t=5) = 7\), \(N_{1} (t=5) = 2\), \(N_{2} (t=5) = 5\) 에 대해
    \(P(w_{1} | t=5) = \frac{2}{7}\), \(P(w_{2} | t=5) = \frac{5}{7}\)
  • node impurity and splitting :
    \(I(t) = \phi (P(w_{1} | t), \cdots, P(w_{c} | t))\) where \(\sum_{i=1}^{c} P(w_{i} | t) = 1\)
    • maximum, minimum :

      • $$P(w_{1}

        t) = \cdots = P(w_{c}

        t) = \frac{1}{c}$$ 일 때 maximum 값 (가장 impure)

      • $$P(w_{j}

        t) = 1\(and\)P(w_{i}

        t) = 0\(for all\)i \neq j$$ 일 때 minimum 값 (가장 pure)

    • 종류 :

      • Gini criterion : $$I(t) = 1 - \sum_{i} P(w_{i}

        t)^{2}$$

      • Entropy : $$I(t) = - \sum_{i} P(w_{i}

        t) \text{log}{2} P(w{i}

        t)$$

      • Classification error : $$I(t) = 1 - \text{max}{i} P(w{i}

        t) = \frac{N_{minor}(t)}{N(t)}$$

    • parent node에서 child node로 옮겼을 때 impurity가 많이 감소할수록 잘 split한 것임
      즉, \(\Delta I(t) = I(t) - (I(t_{L}) \frac{N(t_{L})}{N(t)} + I(t_{R}) \frac{N(t_{R})}{N(t)})\) 가 클수록 better split
      e.g. \(I(t) = 1 - \text{max}_{i} P(w_{i} | t)\) 를 사용할 경우 위의 그림에서 \(\Delta I(t=3) = \frac{3}{13} - (\frac{1}{4} \frac{4}{13} + \frac{0}{9} \frac{9}{13}) = \frac{2}{13}\)
    • terminating splitting :
      • stopping rule :
        stop splitting the node if \(\Delta I(t) \lt \tau\)
      • pruning :
        일단 (nearly) pure class 될 때까지 tree 늘린 뒤
        subtree를 terminal node로 대체

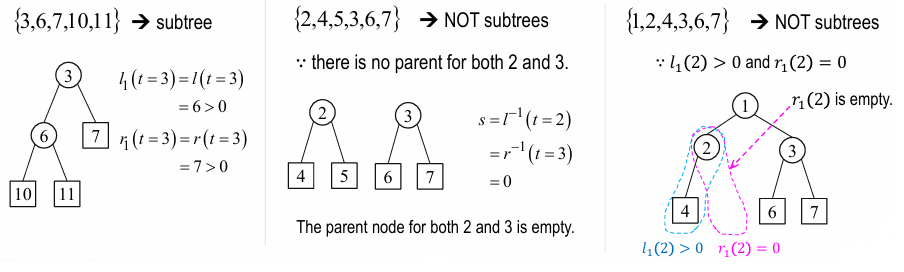
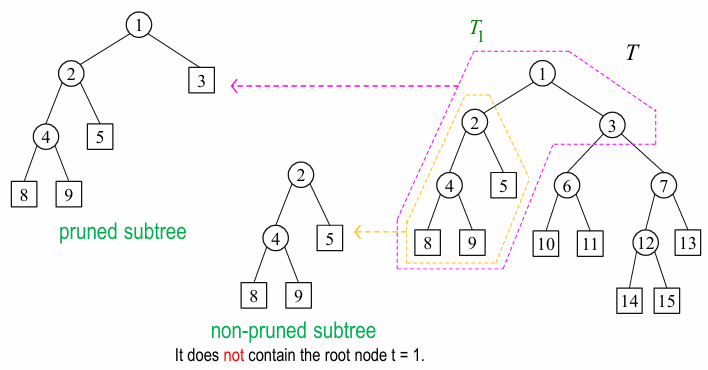
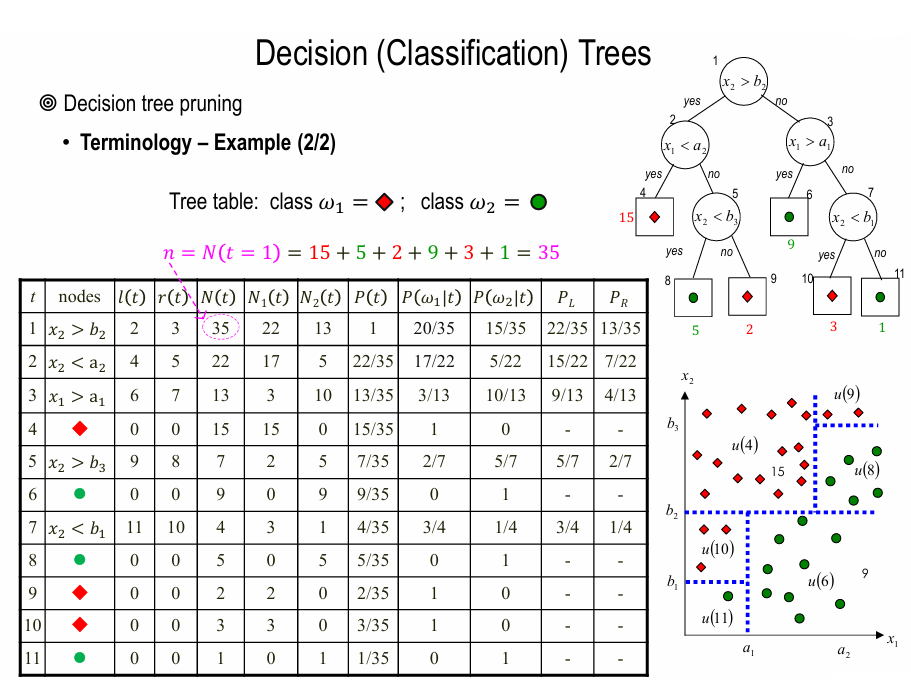
• Pruning Decision Tree :
  • Let’s define
    • \(l(t), r(t)\) : node \(t\) 의 left, right child (\(l(t) = r(t) = 0\) for terminal node \(t\))
    • \(\tilde T\) : set of terminal(leaf) nodes of tree \(T\)
    • \[P(t) = \frac{N(t)}{N(t=1)}\]

    • $$P(w_{j}	t) = \frac{N_{j}(t)}{N(t)}$$
      where $$\sum_{j=1}^{c} P(w_{j}	t) = 1$$

    • \(P_{L}(t) = \frac{P(l(t))}{P(t)} = \frac{N(l(t))}{N(t)}\)
      \(P_{R}(t) = \frac{P(r(t))}{P(t)} = \frac{N(r(t))}{N(t)}\)
      where \(P_{L}(t) + P_{R}(t) = 1\)
  • subtree and pruned subtree :
    • subtree : 하나의 node에서 출발해서 its child node들을 가져오는데 양쪽 다 가져와야 함 (위 그림 참고)
    • pruned subtree \(T_{1} \leq T\) : tree \(T\) 와 root node가 같아야 함 (위 그림 참고)

  • tree \(T\) has class labels $${ w_{j}(t)

    t \in \tilde T }\(and disjoint partition\){ u(t)

    t \in \tilde T }$

• Pruning Algorithm :
  • Let’s define
    • misclassification rate at node \(t\) :
      \(R(t) = \frac{M(t)}{N(t=1)} = \frac{M(t)}{N(t)} \frac{N(t)}{N(t=1)} = r(t) p(t)\)
      (node \(t\) 가 terminal node라고 생각)
      where \(r(t) = \frac{M(t)}{N(t)}\) : classification error at node \(t\)
      where \(p(t) = \frac{N(t)}{N(t=1)}\) : frequency at node \(t\)
    • total misclassification rate for tree \(T\) :
      \(R(T) = \sum_{t \in \tilde T} R(t) = \frac{1}{N(t=1)} \sum_{t \in \tilde T} M(t)\)
      (for all terminal nodes of tree \(T\))
    • cost-complexity at node \(t\) :
      \(R_{\alpha}(t) = R(t) + \alpha\)
    • cost-complexity for tree \(T\) :
      \(R_{\alpha}(T) = \sum_{t \in \tilde T} R_{\alpha} (t) = R(T) + \alpha | \tilde T |\)
    • cost-complexity for subtree \(T_{t}\) :
      \(R_{\alpha}(T_{t}) = \sum_{t \in \tilde T_{t}} R_{\alpha} (t) = R(T_{t}) + \alpha | \tilde T_{t} |\)
      where \(T_{t}\) : node \(t\) 를 root node로 하는 subtree
    • \(\alpha = g(t)\) s.t. \(R_{\alpha}(t) = R_{\alpha}(T_{t})\) :
      \(R_{\alpha}(t) = R_{\alpha}(T_{t})\) 이도록 하는 \(\alpha\)
      즉, \(R(t) + \alpha = R(T_{t}) + \alpha | \tilde T_{t} |\) 이도록 하는 \(\alpha\) 즉, \(\alpha = g(t) = \frac{R(t) - R(T_{t})}{| \tilde T_{t} | - 1}\)
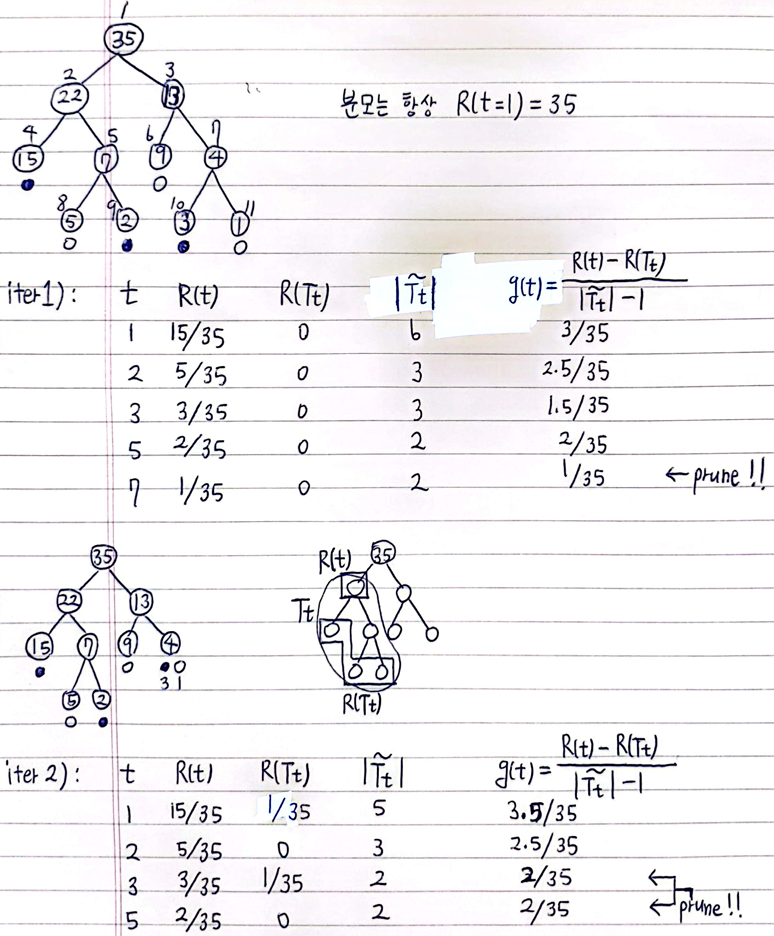
  • Pruning :
    • \(g(t)\) 가 최소인 node \(t\) 를 prune!!
      \(\alpha = g(t) = \frac{R(t) - R(T_{t})}{| \tilde T_{t} | - 1}\) 가 최소라는 말은,
      • case 1)
        node \(t\) 가 terminal node이든 (\(R(t)\)), node \(t\) 아래로 children이 있든 (\(R(T_{t})\)) 차이가 크지 않아서 prune해도 ok
        즉, \(R(t) - R(T_{t})\) 가 작다
      • case 2)
        node \(t\) 아래로 children이 너무 많아서 (large \(| \tilde T_{t} |\)) prune하는 게 나음
    • prune할수록 \(| \tilde T_{t} |\) 가 작아지니까
      tree는 작아지고
      cost \(\alpha = g(t)\) 는 커짐
    • test set 또는 cross-validation 이용해서
      training set에 너무 overfitting된 nodes를 pruning함으로써
      better generalization
• Pruning Example :

Chapter 9. Algorithm-Independent Machine Learning

• Resampling :
  • Comparison :
    • Sampling :
      select groups within population
    • Resampling :
      accuracy 높이고 uncertainty of estimate quantify하기 위해
      reselect new samples, that can provide more info. about population, based on one observed sample
      and estimate population(distribution) param. multiple times from data
  • 종류 :
    resampling 기법 중 유명한 건
    • jackknife
    • bootstrap

How to estimate bias and variance of estimator(statistic)?

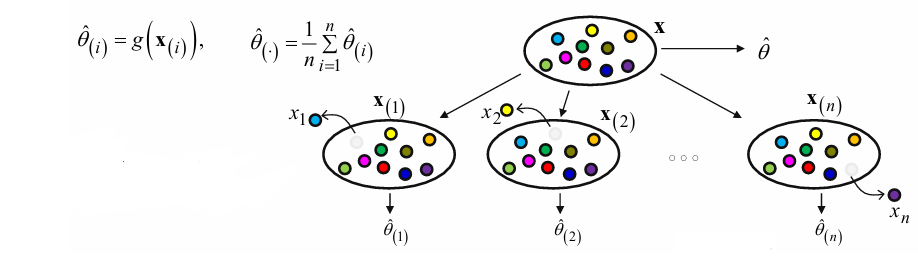
• Jackknife :
  • bias 줄이기 위해
    remove samples from available dataset
    and recalculate the estimator
  • may fail in estimating non-smooth statistic
    (smooth statistic : small change in data causes small change in statistic)
  • \(i\)-th jackknife sample :
    \(i\)-th observation 제거
    \(x_{i} = (x_{1}, \cdots, x_{i-1}, x_{i+1}, \cdots, x_{n})\)
  • estimate again by \(i\)-th jackknife sample :
    estimate \(\hat \theta_{(i)} = g(x_{i})\) based on \(x_{i}\)
  • \(i\)-th pseudo-sample :
    \(\tilde \theta_{(i)} = n \hat \theta - (n-1) \hat \theta_{(i)}\)
  • jackknife estimate of bias (\(\hat b_{jack}(\hat \theta)\)) :
    \(\hat b_{jack}(\hat \theta) = (n-1)(\hat \theta_{(\cdot)} - \hat \theta)\)
    where \(\hat \theta_{(\cdot)} = \frac{1}{n} \sum_{i=1}^{n} \hat \theta_{(i)}\)
  • bias-corrected jackknife estimate :
    \(\hat \theta_{jack} = \hat \theta - \hat b_{jack}(\hat \theta) = n \hat \theta - (n-1) \hat \theta_{(\cdot)} = \frac{1}{n} \sum_{i=1}^{n} \tilde \theta_{i}\)
    Then bias-corrected \(\hat \theta_{jack}\) 은 \(\hat \theta\) 에 비해 bias 작음
  • jackknife estimate of variance (\(\hat v_{jack}(\hat \theta)\)) :
    \(\hat v_{jack} (\hat \theta) = \hat v (\hat \theta_{jack}) = \frac{s_{jack}^{2}}{n} = \frac{1}{n(n-1)} \sum_{i=1}^{n} (\tilde \theta_{(i)} - \frac{1}{n} \sum_{j=1}^{n} \tilde \theta_{(j)})^{2} = \frac{n-1}{n} \sum_{i=1}^{n} (\hat \theta_{(i)} - \hat \theta_{(\cdot)})^{2} = \frac{(n-1)^{2}}{n} s^{2}\)
    where \(s_{jack}^{2}\) is sample variance of \(n\) pseudo-samples
    where \(s\) is sample variance of \(n\) estimates
    (\(Var(\tilde \theta_{(i)}) \approx Var(\sqrt{n} \hat \theta)\))

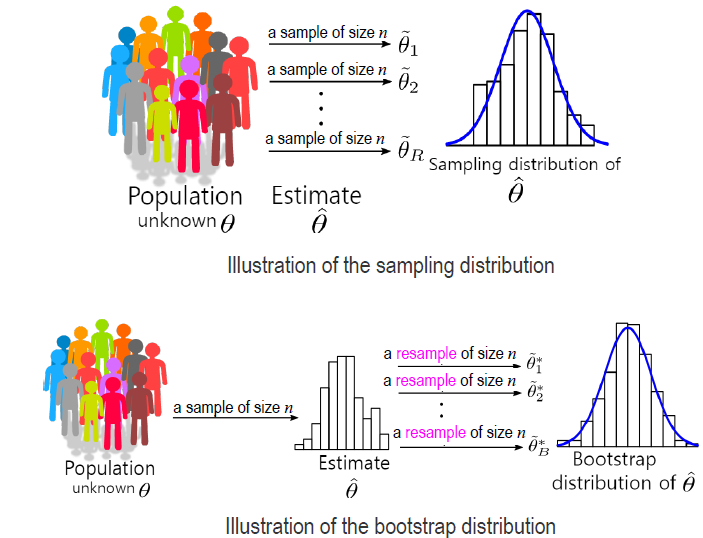
• Bootstrap :
  • sampling distribution (\(\neq\) sample distribution) :
    distribution of estimated statistics from different samples from the same population
    By central limit theorem, sampling distribution is normal and allows for probabilistic predictions about outcomes
    • precision : by standard deviation of sampling distribution
    • accuracy : by bias
  • bootstrap distribution :
    population 대신 a sample set itself로부터 sampling n points with replacement 수행하여 distribution 구함
    (population으로부터 추가 samples generate하지 않아도 new samples (sampling distribution) 얻는 과정을 모방)
  • estimate by \(b\)-th bootstrap sample : \(\hat \theta^{\ast (b)}\)
  • bootstrap estimate of bias (\(b_{boot} (\hat \theta)\)) :
    \(b_{boot} (\hat \theta) = \hat \theta^{\ast (\cdot)} - \hat \theta\)
    where \(\hat \theta^{\ast (\cdot)} = \frac{1}{B} \sum_{b=1}^{B} \hat \theta^{\ast (b)}\)
  • bootstrap estimate of variance (\(Var_{boot} [\hat \theta]\)) :
    \(Var_{boot} [\hat \theta] = \frac{1}{B} \sum_{b=1}^{B} (\hat \theta^{\ast (b)} - \hat \theta^{\ast (\cdot)})^{2}\)
    (As \(B \rightarrow \infty\), \(Var_{boot}[\hat \theta] \rightarrow Var[\hat \theta]\))
  • Implementation : Ensemble learning
    • Step 1)
      multiple subsets(size \(n\)) are selected with replacement from original dataset(size \(n\))
    • Step 2)
      A base model is created on each subset
    • Step 3)
      Each independent model is learned in parallel with each subset
    • Step 4)
      Final prediction by combining predictions of each model
  • 장단점 :
    • 장점 :
      • sampling distribution for statistics의 shape, spread, bias 정도를 estimate하기 좋은 방법
      • small samples로도 잘 작동
        (jackknife는 \(n\) 개의 \(\hat \theta_{(i)}\) 구하려고 반복해야 했음)
      • \(B\) 커질수록 bias, var. 측면에서 더 좋지만 computational load 커짐
    • 단점 :
      • non-smooth model일 때는 잘 작동 X
      • 아래의 경우에는 사용 안 함
        • data가 너무 작아서 population value와 가깝지 않을 때
        • data에 outlier가 너무 많을 때
        • dependent data일 때 (e.g. time series data)
          (bootstrap은 data independence를 가정)
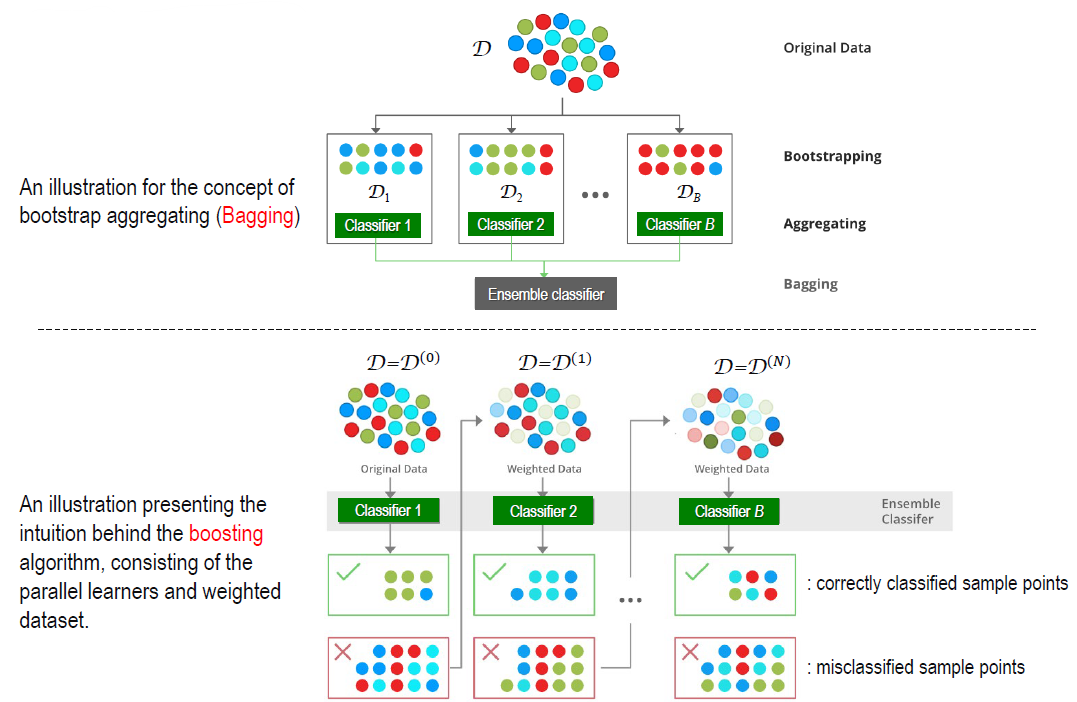
• Ensemble learning에는 Bagging과 Boosting의 two types 있음
  • 공통점 :
    • Ensemble learning
      • to get 1 strong learner from N homogeneous weak learners by averaging or majority voting
        (each weak learner는
        one target class에 대해서는 accurately predict하지만,
        all target classes에 대해서는 not generalized (not optimal) to accurately predict)
  • 차이점 :
    individual weak learner의 training phase에 차이가 있음
    • Bagging (= Bootstrap aggregating) :
      learn from each other independently in parallel, and combine them by averaging or voting
      • aim to decrease variance (not bias)
        (overfitting 문제 해소)
      • combine predictions that belong to the same type
      • models combine할 때 equal vote
      • each model is independent
      • different training subsets : random sample from entire training dataset
        by resampling with replacement
      • classifier가 unstable (e.g. decision tree) (high variance) 하더라도 improve in almost all cases
      • built and trained in parallel
      • e.g. random forest model
    • Boosting (Arcing = Adaptive resampling and combining) :
      learn iteratively and sequentially and adaptively
      first round에는 training examples를 equal weight로 반영한 뒤
      round마다 misclassified training examples(by current weak hypothesis) 에 더 많은 weight를 부여하도록 update하여
      next round에서 weak learner가 hard-to-classify examples에 더 집중하도록 함
      • aim to decrease bias (not variance)
      • combine predictions that belong to the different types
      • models combine할 때 weighted vote by their performance (accuracy)
      • new model is influenced by the performance of previous model
      • every new training subset : weighted sample to focus on misclassified examples by previous models (more often chosen)
        by adaptive resampling 그로써 weak learner can be converted to strong learner
      • classifier가 stable하고 simple할 때 (high bias) 적용
      • built and trained sequentially
      • e.g. AdaBoost

Chapter 10. Unsupervised Learning

• unsupervised learning :
  hard since no answer and no correct accuracy measure to check
  but, needed since annotating is costly and we often don’t know how many classes there are
  • parametric unsupervised learning :
    • sample comes from population that follows fixed param. probability distribution
    • GMM(Gaussian Mixture Model) and EM(Expectation-Maximization)
  • non-parametric unsupervised learning :
    • clustering
    • distribution-free, so do not require assumption about population distribution

• K-means clustering :
  discriminative approach

• GMM(Gaussian Mixture Model) :
  generative approach
  • mixture density :
    \(p(x_{k} | \theta) = \sum_{j=1}^{c} P(w_{j}) p(x_{k} | w_{j}, \theta_{j})\)
    where \(\sum_{j=1}^{c} P(w_{j}) = 1\)
    (gaussian일 경우 \(p(x_k | w_{i}, \theta_{i}) = N(x_k | w_{i}, \mu_{i}, \Sigma_{i}) = (2 \pi)^{-\frac{d}{2}} | \Sigma_{i} |^{-\frac{1}{2}} \text{exp}(-\frac{1}{2}(x_k - \mu_{i})^T \Sigma_{i}^{-1} (x_k - \mu_{i}))\))
  • matrix derivative :
    \(\frac{d}{dx}(Ax) = A\)
    \(\frac{d}{dx}(y^TAx) = A^Ty\)
    \(\frac{d}{dx}(x^TAx) = (A+A^T)x\)
    \(\frac{d}{dA}(x^TAx) = xx^T\)
    \(\frac{\partial |A|}{\partial A} = (\text{adj}(A))^T = |A|(A^{-1})^T\)
    \(\frac{\partial \text{ln}|A|}{\partial A} = (A^{-1})^T = (A^T)^{-1}\) where \(|A| = \frac{1}{|A^{-1}|}\)
  • MLE on \(\theta\) :
    \(L = \text{ln} p(D | \theta) = \text{ln} \prod_{k=1}^{n} p(x_{k} | \theta) = \sum_{k=1}^{n} \text{ln} p(x_{k} | \theta)\)
    \(\rightarrow\)
    data point index \(k\), class index \(i\) 에 대해
    \(\nabla_{\theta_{i}} L = \cdots = \sum_{k=1}^{n} \gamma_{ki} \nabla_{\theta_{i}} \text{ln} p(x_{k} | w_{i}, \theta_{i}) = 0\)
    where \(\gamma_{ki} = \frac{p(x_{k} | w_{i}, \theta_{i}) P(w_{i})}{\sum_{j=1}^{c} p(x_{k} | w_{j}, \theta_{j}) P(w_{j})} = \frac{p(x_{k} | w_{i}, \theta_{i}) P(w_{i})}{p(x_{k} | \theta)} = P(w_{i} | x_{k}, \theta_{i})\) : posterior probability (responsibility of mixture component \(i\) for data \(x_{k}\))
    (data \(x_{k}\) 가 cluster \(i\) 에 속할 확률)
    • Case 1) unknown \(\theta_{i} = \mu_{i}\) :
      \(\sum_{k=1}^{n} \gamma_{ki} \nabla_{\mu_{i}} \text{ln} p(x_{k} | w_{i}, \theta_{i}) = 0\)
      \(\rightarrow\)
      \(\hat \mu_{i} = \frac{1}{\sum_{k=1}^{n} \gamma_{ki}} \sum_{k=1}^{n} \gamma_{ki} x_{k} = \frac{1}{n_{i}} \sum_{k=1}^{n} \gamma_{ki} x_{k}\) : weighted mean of data points where posterior is weight
      where \(n_{i} = \sum_{k=1}^{n} \gamma_{ki}\) : effective(expected) number of points assigned to cluster \(i\)
    • Case 2) unknown \(\mu_{i}\) and \(\Sigma_{i}\) :
      \(\sum_{k=1}^{n} \gamma_{ki} \nabla_{\Sigma_{i}^{-1}} \text{ln} p(x_{k} | w_{i}, \theta_{i}) = 0\)
      \(\rightarrow\)
      \(\hat \Sigma_{i} = \frac{1}{\sum_{k=1}^{n} \gamma_{ki}} \sum_{k=1}^{n} \gamma_{ki} (x_{k} - \hat \mu_{i})(x_{k} - \hat \mu_{i})^{T} = \frac{1}{n_{i}} \sum_{k=1}^{n} \gamma_{ki} (x_{k} - \hat \mu_{i})(x_{k} - \hat \mu_{i})^{T}\)
    • Case 3) unknown \(\mu_{i}\) and \(\Sigma_{i}\) and \(P(w_{i})\) :
      \(\hat P(w_{i}) = \frac{n_{i}}{n}\)
      (proof는 아래에)
      (\(P(w_{i})\) 와 \(\gamma_{ki}\) 는 서로 dependent,
      so, \(\hat \mu_{i}, \hat \Sigma_{i}, \hat P(w_{i})\) 는 no closed-form solution
      so, need repetitive steps)

• EM (Expectation-Maximization) :
  repeat E-step and M-step until log-likelihood \(L\) converges
  • E-step :
    for each data point \(x_{k}\), estimate posterior \(\gamma_{ki}\) and assign \(x_{k}\) to the class \(\text{max}_{i} \gamma_{ki}\)
  • M-step :
    update parameter \(\hat \theta\)
    e.g. \(\hat \mu_{i}, \hat \Sigma_{i}, \hat P(w_{i})\)

Cheet Sheet for Final Exam