PhysGaussian

Physics-Integrated 3D Gaussians for Generative Dynamics (CVPR 2024)

PhysGaussian - Physics-Integrated 3D Gaussians for Generative Dynamics

Tianyi Xie, Zeshun Zong, Yuxing Qiu, Xuan Li, Yutao Feng, Yin Yang, Chenfanfu Jiang

paper :
https://arxiv.org/abs/2311.12198
project website :
https://xpandora.github.io/PhysGaussian/
code :
https://github.com/XPandora/PhysGaussian
reference :
https://xoft.tistory.com/101

Contribution

• Physics Simulation을 3DGS에 결합 :
  • 3DGS에 부피, 질량, 속도 (Physics) property를 부여하여
    3DGS의 covariance 및 rotation matrix가 시간에 따라 물리 법칙에 따라 변화
  • MPM simulation 장점과 3DGS rendering 장점을 결합하여
    unified simulation-rendering pipeline 제시

결과 영상이 재밌음!

Overview

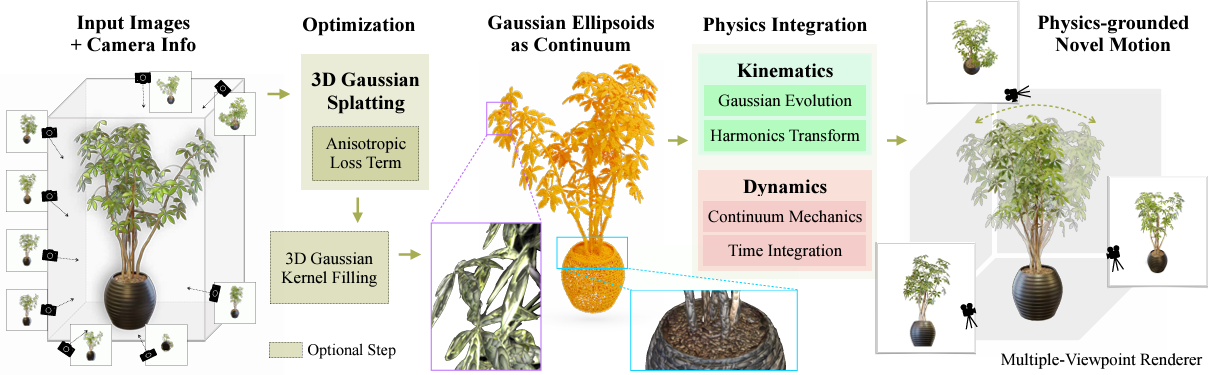
• Step 1) 3DGS optimization
  Anisotropic Loss를 추가하여 3DGS를 둥글둥글하게 만듦
• Step 2) 3DGS Internel Filling
  Object 내부 공간을 3DGS로 채워서 continuum(연속체)로 만듦
• Step 3) Physics Integration
  • Dynamics :
    3DGS에 부피, 질량 부여하여
    시간에 따라 Continuum Mechanics(연속체 역학)이라는 물리 법칙 따르도록 함
  • Kinematics :
    Gaussian Evolution, SH Transform을 통해
    시간에 따른 물리적인 변화를 3DGS로 모델링

Backgrounds on Continuum Mechanics

• Conservation of Mass (질량 보존 법칙) :
  시간 \(t\) 가 바뀌어도 infinitesimal region 내 질량은 항상 일정하게 유지된다!!
  \(\int_{B_{\epsilon}^{t}} \rho (x, t) = \int_{B_{\epsilon}^{0}} \rho (\phi^{-1}(x, t), 0)\)
  • \(B_{\epsilon}^{t}\) : infinitesimal region at \(t\)
  • \(\rho(x, t)\) : density field at \(x, t\)
  • \(x = \phi(x_{0}, t)\) : deformation map from \(x_{0}, 0\) to \(x, t\)
• Conservation of Momentum (운동량 보존 법칙) :
  시간 \(t\) 가 바뀌어도 물질의 운동량은 변하지 않는다!!
  운동량 변화량 : \(\rho(x, t) \overset{\cdot}{v}(x, t) = \nabla \cdot \sigma(x, t) + f^{ext}\)
  • \(\overset{\cdot}{v}(x, t)\) : 가속도 field at \(x, t\)
  • \(\sigma = \frac{1}{det(F)}\frac{\partial \psi}{\partial F}F^{E}(F^{E})^{T}\) : Cauchy stress tensor (물체 내부에서 발생하는 응력)
    where \(\psi(F)\) : hyperelastic energy density
    where deformation field gradient \(F = F^{E} F^{P}\)
    • \(F^{E}\) : elastic part (탄성)
      물체에 stress를 가해서 조직에 구조적인 변형이 발생한 후,
      stress를 제거했을 때 원래 상태로 되돌아가는 성질
    • \(F^{P}\) : plastic part (소성)
      물체에 stress를 가해서 조직에 구조적인 변형이 발생한 후,
      stress가 탄성 범위를 넘어가서
      stress를 제거하더라도 원래 상태로 되돌아오지 않는 성질
  • \(f^{ext}\) : external force per unit volume

MPM (Material Point Method)

• 핵심 :
  particle과 grid 간에 운동량이 상호작용하여
  이 과정에서 질량과 운동량이 보존되어
  simulation 했을 때 현실과 비슷
  • Lagrangian Particle Domain :
    particle의 위치, 질량, 운동량, 응력, 부피, 외력 등을 모델링하고
    particle 별로 추적하여 update
  • Eulerian Grid Domain :
    공간을 3D grid로 나누어서 grid를 통해 particle 이동
    cell의 크기가 작아질수록 정확도는 올라가지만 연산속도는 느려짐

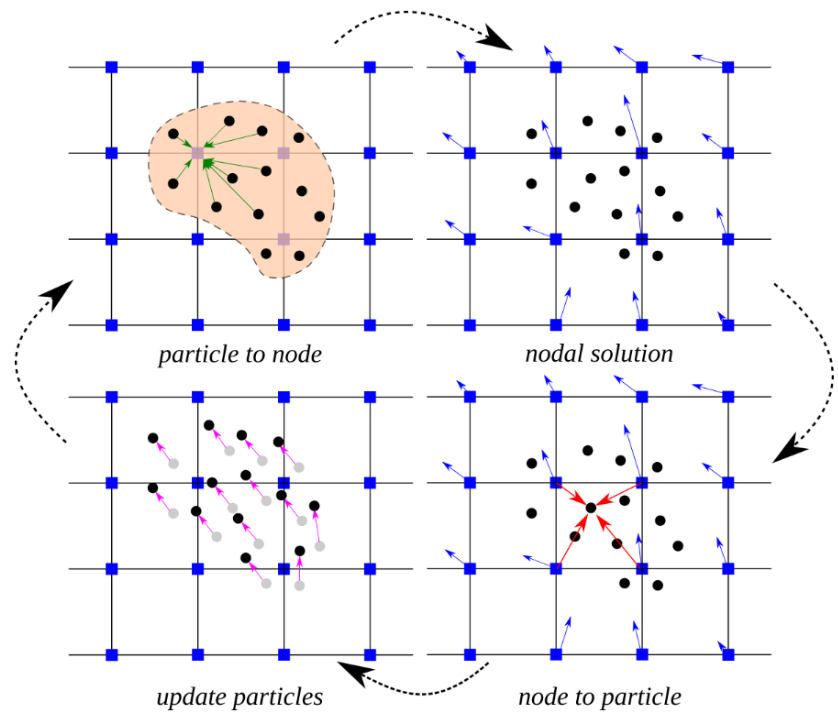
• Procedure :
  • Particle to Node :
    each particle의 물리량을 grid 상의 adjacent 8 nodes로 분배
  • Nodal Solution :
    집계된 힘을 이용해서 each node의 \(a = \frac{F}{m}\), \(v\) 를 update
  • Node to Particle :
    each node의 \(a, v\) 를 particle로 전파 by weighted sum
  • Update Particles :
    each particle의 \(a, v\) 이용해서 새로운 particle 위치 갱신

실험 예시 : SIGGRAPH2018

Physics-Integrated 3DGS

그렇다면 어떻게 물리 법칙을 3DGS에 적용할까??

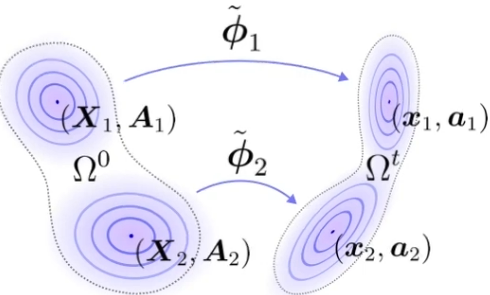
• 방법 1) deformation gradient \(F_{p}\) 로 approx.
  • local affine transformation of deformation map \(\phi\) :
    \(\tilde \phi (X, t) = x_{p} + F_{p} (X - X_{p})\)
    • \(X\) : arbitrary point
    • \(X_{p}\) : particle \(p\) 의 initial point
    • \(x_{p}\) : particle \(p\) 의 current point
    • \(F_{p}\) : 점이 어떻게 이동하는지에 대한 deformation gradient matrix
      (물리 법칙 적용)
  • 3DGS position, covariance matrix 변화 :
    By approx. deformation map,
    \(x_{p}(t) = \tilde \phi (X_{p}, t)\)
    \(\Sigma_{p}(t) = F_{p}(t) \Sigma_{p} F_{p}(t)^{T}\)
  • Gaussian 수식 변화 :
    \(G_{p}(x, t) = e^{-\frac{1}{2}(x-x_{p})^{T}(F_{p}(t) \Sigma_{p} F_{p}(t)^{T})^{-1}(x-x_{p})}\)
  • grid 부피를 particle 수로 나누어서 각 particle 부피 \(V_{p}^{0}\) 를 초기화하고
    이로써 각 particle(Gaussian)은 질량 \(m_{p} = \phi_{p} V_{p}\) 를 가지게 되고
    MPM Simulation을 바탕으로 Gaussian이 물리 법칙을 따름
  • 아래의 이유로 Physics와 3DGS의 결합은 자연스러움
    • Gaussian itself가
      Continuum의 discretized form으로 간주되므로
      직접 simulation 가능
    • 물리 법칙에 의해 변형된 Deformed Gaussian은
      3DGS rasterization에 의해
      직접 rendering 가능
    • 따라서 WS2(What you see is What you simulate) 달성
• 방법 2) incremental update
  • deformation gradient \(F_{p}\) 에 의존하지 않고
    Langrangian framework(MPM simulation)에 더 잘 맞는
    Gaussian Kinematic(운동학) 방법 제시
  • computational fluid dynamics (전산 유체 역학)에 따라
    • covariance matrix :
      covariance matrix는 discretize되어
      \(\Sigma_{p}(t) = F_{p}(t) \Sigma_{p} F_{p}(t)^{T}\)
      대신
      \(\Sigma_{p}^{n+1} = \Sigma_{i}^{n} + \Delta t \overset{\cdot}{\Sigma_{p}^{n}} = \Sigma_{i}^{n} + \Delta t (\nabla v_{p} \Sigma_{p}^{n} + \Sigma_{p}^{n} \nabla v_{p}^{T})\)
    • rotation matrix :
      마찬가지로 \(R_{p}^{0} = I\) 에서 출발해서 비슷하게 update 가능
    • 즉, covariance matrix와 rotation matrix가 물리 법칙을 따르면서 incrementally update되도록 설계!!
  • 위의 수식을 통해 deformation gradient \(F_{p}\) 를 직접 구하지 않더라도
    Gaussian covariance를 \(t^{n}\) 에서 \(t^{n+1}\) 으로 incremental update 가능

Orientation of SH

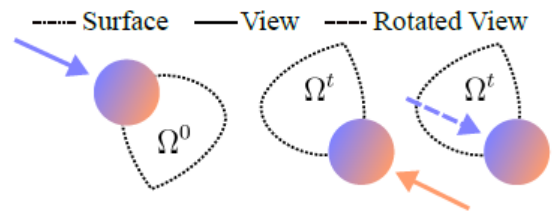
• SH는 view direction에 따른 color를 모델링하는, hard-coding되어 있는 함수이다
  따라서 시간 \(t\) 에 따라 particle(Gaussian)이 rotate하면 색깔이 전혀 달라지므로
  view direction에 particle(Gaussian)의 역회전을 적용
  • particle(Gaussian)의 회전 정보 :
    surface orientation을 사용한 Point-NeRF 와 달리
    방법 1)의 경우 polar decomposition을 통해 deformation gradient \(F_{p} = R_{p}S_{p}\) 에서 \(R_{p}\) 추출해서 사용
    방법 2)의 경우 polar decomposition을 통해 \((I + \Delta t v_{p}) R_{p}^{n}\) 에서 \(R_{p}^{n+1}\) 추출해서 사용

Internal Filling

• recon. Gaussians는 surface 근처에 분포하는 경향이 있으므로
  object의 내부 구조는 비어 있는 채로 surface에 가려져 있음
  \(\rightarrow\)
  object의 deformation이 클 경우 내부가 노출될 수도 있고
  질량을 가지는 물리 법칙에 따르는 volumetric object으로 만들기 위해
  비어 있는 내부 영역도 particles(Gaussians)로 채워야 함

• Internal Filling :
  • Step 1)
    discretize
    from continuous 3D opacity field \(d(x) = \sum_{p} \sigma_{p} e^{-\frac{1}{2}(x-x_{p})^{T}\Sigma_{p}^{-1}(x-x_{p})}\)
    into discrete 3D grid
  • Step 2)
    low opacity(\(\sigma_{i} \lt \sigma_{th}\))를 가지는 grid에서
    high opacity(\(\sigma_{j} \gt \sigma_{th}\))를 가지는 grid로
    ray가 통과할 때
    이를 intersection이라고 하자
  • Step 3)
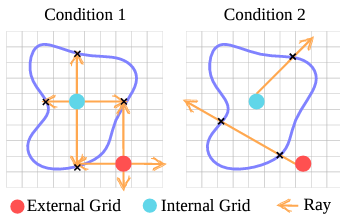
    아래 두 가지 조건을 만족할 때 object 내부에 있다고 간주하고 3DGS 생성
    • Condition 1) :
      3D grid 상에서 6 axes 방향으로 ray casting한 뒤
      object 내부에 있는 grid의 경우 항상 surface와 intersect할 것이므로
      intersection 개수가 6개인지 체크하여 candidate grids 선택
    • Condition 2) :
      candidate grids를 refine하기 위해
      additional ray를 casting하여 intersection 개수 체크
  • Step 4)
    object 내부에 채워 넣은 gaussian들도 3D 상에서 visualize할 필요가 있을 수 있음
    internal-filled particle(Gaussian)의 경우
    opacity \(\sigma_{p}\) 와 color \(C_{p}\) 는 closest Gaussian의 것을 물려받고
    covariance matrix는 \(\text{diag}(r_{p}^{2}, r_{p}^{2}, r_{p}^{2})\) 으로 initialize
    where \(r_{p}\) : particle radius from its volume \(V_{p}^{0} = \frac{4 \pi r_{p}^{3}}{3}\)
    (본 논문의 저자는 시도하지 않았지만 internal filling을 위해 generative model을 사용하면 more realistic results 가능할 듯)

Anisotropy Regularizer

• 3DGS가 너무 얇을 경우
  large deformation일 때 Gaussian이 object surface의 바깥쪽으로 튀어나와
  plush artifacts 발생 가능

chair에 Twist deformation 가했을 때 생기는 plush artifacts

• \(L_{aniso} = \frac{1}{| P |} \sum_{p \in P} \text{max}(\frac{\text{max}(S_{p})}{\text{min}(S_{p})}, r) - r\)
  where \(S_{p}\) : scale matrix of 3DGS
  • \(\frac{\text{max}(S_{p})}{\text{min}(S_{p})} \leq r\)
    즉, 장축과 단축의 길이 비가 threshold \(r\) 을 넘지 않도록
    3DGS를 둥글둥글하게 만듦

Experiments

• Dataset :
  InstantNGP, NerfStudio, DroneDeployNeRF, \(\cdots\)

• Resource :
  24-core 3.50GHz Intel i9-10920X machine with Nvidia RTX 3090 GPU

• MPM Simulation :
  • MPM :
    SIGGRAPH2023
  • simulation region :
    simulation region을 manually 선택하여 \(2 \times 2 \times 2\) cube로 normalize한 뒤 3D dense crid로 discretize
  • particle :
    controlled movement(흔들리는 여우 얼굴 등)를 보일 specific particles만 선택적으로 velocities 수정하고
    나머지 particles는 물리 법칙을 따르는 natural motion
• Qualitative Results :
  Video 를 보면
  Simulation 할 때
  • Fox의 경우
    물체의 원래 형태로 되돌아가는 Elasticity (탄성) 성질을 적용
  • Plane의 경우
    물체의 원래 형태로 되돌아가지 않는 Metal (금속) 성질을 적용
  • Ruins의 경우
    Sand 효과 (granular-level frictional effect based on Druker-Prager plastic model)를 적용
  • Toast의 경우
    MPM Simulation에 따라 큰 deformation이 발생하면 입자가 여러 그룹으로 분리되는 Fracture
  • Jam의 경우
    Paste 효과 (non-Newtonian fluid based on Herschel Bulkley plastic model)를 적용

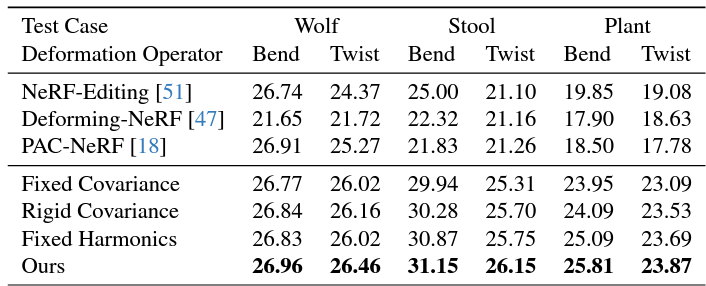
• Quantitative Results :
  • deformation에 대한 GT를 만들기 위해
    BlenderNeRF로 scene 합성한 뒤 lattice deformation tool로 Bend 및 Twist
  • 3가지 model과 비교
    • NeRF-Editing :
      • NeuS 로 추출한 surface mesh를 이용해서 NeRF 를 변형하는데,
        surface recon.에 초점이 맞춰진 연구여서 volumetric simulation과 결합했을 때
        rendering 퀄리티가 낮았음
      • deformation이 extracted surface mesh와 dilated cage mesh의 정밀도에 의존하는데
        mesh가 지나치게 크면 경계가 공백이 될 수 있음
    • Deforming-NeRF :
      • 고해상도 deformation cage mesh를 사용해서 변형하여 향상된 결과 보이지만
        interpolation 과정에서 local detail을 filtering하면서 성능 낮아짐
    • PAC-NeRF :
      • 단순한 object, texture를 표현하도록 디자인되어
        particle representation을 통해 flexible하지만 rendering 퀄리티는 여전히 높지 않음
  • Ours :
    zero-order info.(deformation map)와 first-order info.(deformation gradient)를 모두 활용하였으므로
    deformation 후에도 높은 성능 보임
  • Ablation Study :
    • Fixed Covariance :
      3DGS에 translation만 적용하여
      covariance는 그대로 사용
    • Rigid Covariance :
      3DGS에 rigid transformation 적용하여
      covariance를 수정하여 물리 법칙을 따르도록
    • Fixed Harmonics :
      SH에서 view direction을 rotate하지 않음

논문에서 언급한 기법들을 적용하지 않을 경우 Gaussian이 surface를 제대로 덮지 않아 artifacts 발생

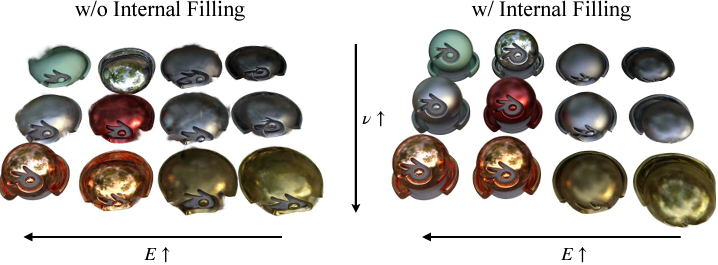
E는 elasticity(탄성도), v는 poission ratio(volume 보존 정도)

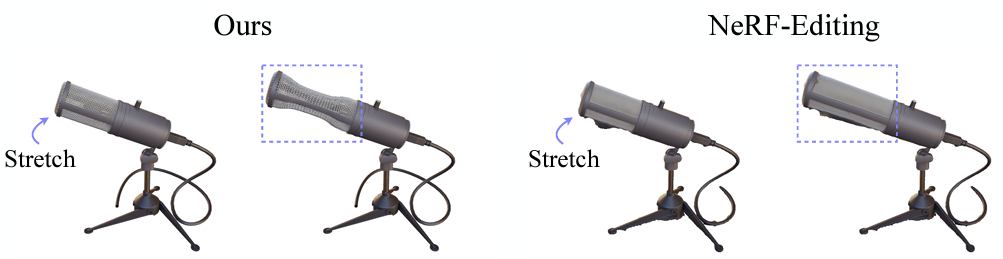
당겼을 때 Physics-based Ours는 물리 법칙에 따라 volume을 잘 보존하지만, Geometry-based NeRF-Editing은 volume 보존하지 않음

Conclusion

• Limitation :
  • 그림자 고려 안 함
  • material param.를 manually 정해주어야 함
    (GS segmentation과 differentiable MPM simulator를 결합하여 video로부터 param. 자동 assign 가능하긴 함)
• Future Work :
  • more versatile materials like liquid 다루기
  • more intuitive user control 포함하기
  • LLM 기술 적용하기
  • geometry-aware 3DGS recon. 결합하여 generative dynamics (생성 동역학) 향상시키기
• 마무리하며..
  3DGS와 전혀 다른 분야를 통합하는 논문들이 종종 나오는데
  이 논문도 결과가 재미있게 나온 논문이었다!!