3D Rotation-Quaternion

Quaternion for Rotation Matrix

Lecture 06: 3D Rotations and Complex Representations (CMU 15-462/662)

referenced video :
3D Rotations and Quaternion
referenced blog :
Quaternion

3D Rotation

• 2D rotation에서는 order of rotations 노상관, but
  3D rotation에서는 order of rotations 중요

Gimbal Lock

• Gimbal Lock :
  Euler angles \(\theta_{x}, \theta_{y}, \theta_{z}\) 로 회전시킬 때 두 축이 맞물려서 한 축이 소실되는 상황

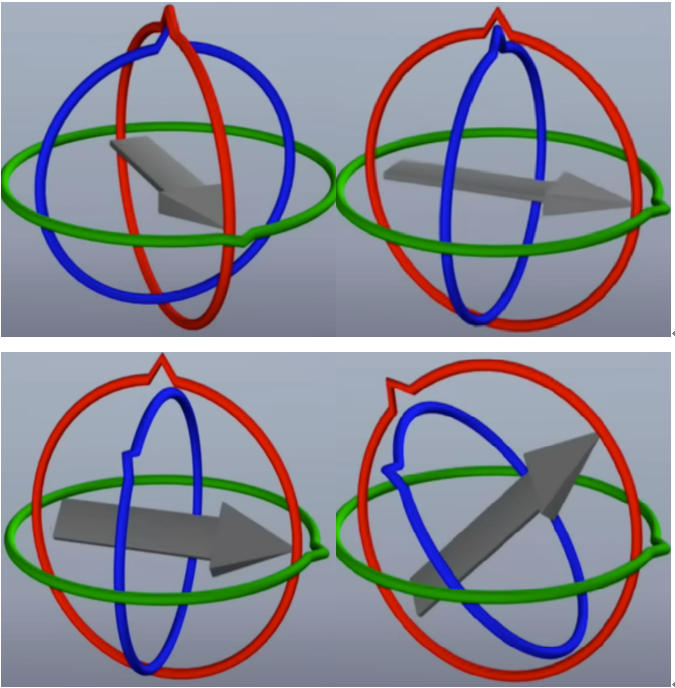
1 -> 2번째 그림 : x축(초록) 회전 / 2 -> 3번째 그림 : z축(파랑) 회전 / 3 -> 4번째 그림 : y축(빨강) 회전

• 위의 그림에 따르면 Euler angles는 \(x\)(초록), \(y\)(빨강), \(z\)(파랑) 순으로 상속관계여서
  \(x\)축(초록)을 회전시키면 그의 자식들인 \(y, z\)축(빨강, 파랑)도 같이 회전한다.

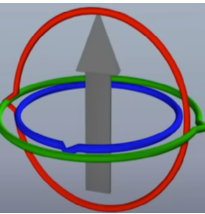
• 이 때, Gimbal Lock은 위의 그림과 같이
  상속관계에서의 2번째 축(빨강)이 -90도 혹은 90도 회전했을 때
  상속관계에서의 1번째 축(초록)과 3번째 축(파랑)이 겹쳐서 같은 방향으로 회전하기 때문에 발생한다.

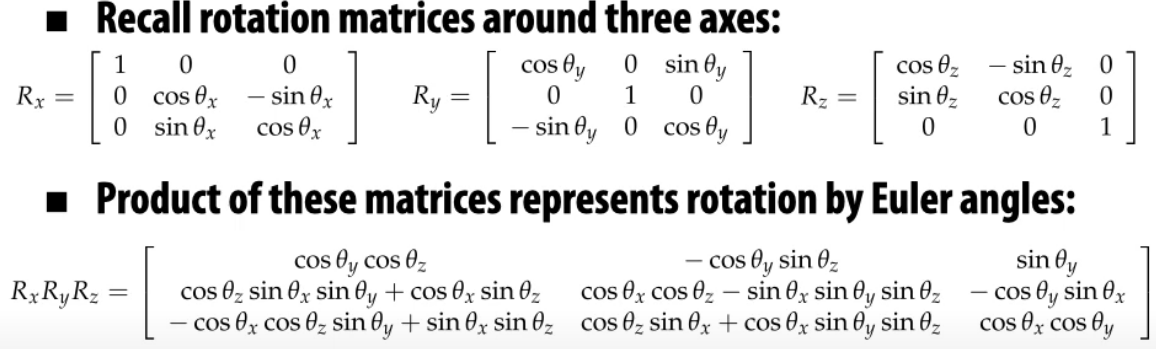
• 예를 들어, 만약 \(\theta_{y} = \frac{\pi}{2}\) 로 고정한다면
  \(R_x R_y R_z = \begin{bmatrix} 0 & 0 & 1 \\ sin(\theta_{x}+\theta_{z}) & cos(\theta_{x}+\theta_{z}) & 0 \\ - cos(\theta_{x}+\theta_{z}) & sin(\theta_{x}+\theta_{z}) & 0 \end{bmatrix}\)
  이므로 \(\theta_{x}, \theta_{z}\) 값(자유도=2)과 관계없이 특정 하나의 axis에 대한 회전(자유도=1)으로 제약 생겨버림!

Quaternion

• Euler angles vs Quaternion :
  Euler angles는 상속관계이므로 한 번에 계산이 불가능하여 순서대로 회전시켜야 하고, 짐벌락 현상이 발생할 수 있지만
  Quaternion은 한 번에 계산 가능하여 동시에 회전시킬 수 있으며, 짐벌락 현상이 없다!

• 2D rotation :
  • real, rectangular form : 2D rotation matrix 복잡
  • complex, polar form : 단순히 크기 곱하고, 각도 더하고!
• 3D rotation :
  • real, xyz form : 3D rotation matrix 복잡
  • quaternion : only need FOUR coordinates!(one real, three imaginary)
    \(H\) = span(\(\{1, i, j, k\}\))
    \(q = a + bi + cj + dk \in H\)
    \(i^2 = j^2 = k^2 = ijk = -1\) \(\leftarrow\) new property!
    \(ij = k\), \(ji = -k\)
    \(jk = i\), \(kj = -i\)
    \(ki = j\), , \(ik = -j\)
• Quaternion :
  • distributive and associative
  • not commutative : \(qp \neq pq\) for \(q, p \in H\)
  • quaternion is a pair of scalar and vector
    \(q = a + bi + cj + dk\)
    \(= (a, \boldsymbol u) = (a, (b, c, d)) \in H\)
    where \(a \in Re(H) = R\) and \(\boldsymbol u \in Im(H) = R^3\)
  • quaternion product :
    • \((a, \boldsymbol u)(b, \boldsymbol v) = (ab - \boldsymbol u \cdot \boldsymbol v, a \boldsymbol v + b \boldsymbol u + \boldsymbol u \times \boldsymbol v)\)
      Equivalently,
      \((a, (x_1, y_1, z_1))(b, (x_2, y_2, z_2)) = (w_1 w_2 - x_1 x_2 - y_1 y_2 - z_1 z_2, (w_1 x_2 + x_1 w_2 + y_1 z_2 - z_1 y_2, w_1 y_2 - x_1 z_2 + y_1 w_2 + z_1 x_2, w_1 z_2 + x_1 y_2 - y_1 x_2 + z_1 w_2))\)
    • \[\boldsymbol u \boldsymbol v = \boldsymbol u \times \boldsymbol v - \boldsymbol u \cdot \boldsymbol v\]
  • quaternion conjugate :
    \(q = (w, x, y, z)\)
    \(q^{\ast} = (w, -x, -y, -z)\)
    \(\| q \| = \sqrt{w^2 + x^2 + y^2 + z^2}\)
    \(q \cdot q^{\ast} = (w, x, y, z) \cdot (w, -x, -y, -z) = w^2 + x^2 + y^2 + z^2 = \| q \|^2\)
    \(q^{-1} = \frac{q^{\ast}}{\| q \|^2} = \frac{q^{\ast}}{q \cdot q^{\ast}} = \frac{1}{q}\)
    \((q_1 q_2)^{\ast} = q_2^{\ast} q_1^{\ast}\)
• 3D Transformations via Quaternions :
  • 3D Rotation : \(x\)를 \(u\)에 대해 \(\theta\)만큼 회전하고 싶다면
    \(q x \bar q\)
    for \(q = cos(\frac{\theta}{2}) + sin(\frac{\theta}{2})u\)
    where pure imaginary 3D vector \(x, u \in Im(H) = R^3\)
    where unit quaternion \(q \in H = (R, R^3)\) where \(\| q \|^2 = 1\)
    where \(\bar q\) 는 \(q\)의 conjugate
  • Interpolating Rotation :
    interpolating Euler angles는 strange-looking paths 및 non-uniform rotation speed를 야기할 수 있음
    대신 Quaternion으로 나타내면,
    spherical linear interpolation (SLERP) :
    Slerp(\(q_0, q_1, t\)) = \(q_0(q_0^{-1} q_1)^t\)
    where \(t \in [0, 1]\)
  • Generating Coordinates for Texture Maps :
    (hyper)complex numbers는 angle-preserving(conformal) maps에 쓰임!
    texture에서 angle-preserving 특성은 사람 눈으로 보기에 매우 그럴 듯하게 보이게 함

• Beyond Quaternion … :
  Lie algebras and Lie Groups 으로도 3D rotations를 나타낼 수 있으며,
  특히 statistics(averages) of rotations 를 구할 때 매우 유용!
  exponential map : axis/angle \(\rightarrow\) rotation matrix
  logarithmic map : rotation matrix \(\rightarrow\) axis/angle

• 4 \(\times\) 1 quaternion \(q\) 으로 3 \(\times\) 3 rotation matrix 만드는 방법 : build_rotation(r)

  def build_rotation(r):
    norm = torch.sqrt(r[:,0]*r[:,0] + r[:,1]*r[:,1] + r[:,2]*r[:,2] + r[:,3]*r[:,3])
    q = r / norm[:, None] # use normalized quaternion
  
    R = torch.zeros((q.size(0), 3, 3), device='cuda')
  
    r = q[:, 0]
    x = q[:, 1]
    y = q[:, 2]
    z = q[:, 3]
  
    R[:, 0, 0] = 1 - 2 * (y*y + z*z)
    R[:, 0, 1] = 2 * (x*y - r*z)
    R[:, 0, 2] = 2 * (x*z + r*y)
    R[:, 1, 0] = 2 * (x*y + r*z)
    R[:, 1, 1] = 1 - 2 * (x*x + z*z)
    R[:, 1, 2] = 2 * (y*z - r*x)
    R[:, 2, 0] = 2 * (x*z - r*y)
    R[:, 2, 1] = 2 * (y*z + r*x)
    R[:, 2, 2] = 1 - 2 * (x*x + y*y)
    return R