SuGaR

Surface-Aligned Gaussian Splatting for Efficient 3D Mesh Reconstruction and High-Quality Mesh Rendering (CVPR 2024)

SuGaR: Surface-Aligned Gaussian Splatting for Efficient 3D Mesh Reconstruction and High-Quality Mesh Rendering

Antoine Guédon, Vincent Lepetit

paper :
https://arxiv.org/abs/2311.12775
project website :
https://anttwo.github.io/sugar/
code :
https://github.com/Anttwo/SuGaR
reference :
NeRF and 3DGS Study

Abstract

• surface 점 sampling :
  surface 근처의 점 \(p\) 를
  Gaussians의 곱 분포로 sampling

• regularization term :
  3DGS가 surface 잘 나타내도록 (well-distributed) 하기 위해
  density function 또는 SDF로 regularization loss term

• obtain mesh using level set points :
  점 \(p\) 주위(\(3 \sigma (v)\))의 points를 sampling하고
  density 계산하여 oriented level set points 구한 뒤
  Poisson equation으로 mesh 구함

• mesh refinement :
  triangle mesh에 new Gaussians binding하여
  mesh optimize할 때 new Gaussians도 함께 optimize

Surface-Aligned 3DGS

Regularization

• 문제 :
  3DGS는 unstructured
  \(\rightarrow\) surface 나타내지 않음

• 해결 :
  regularization loss term
  \(\rightarrow\) 3DGS가 well-distributed and aligned with surface (flat)

  • well-distributed :
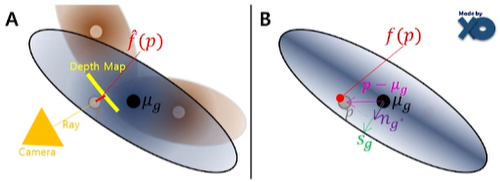
    • Gaussians끼리 overlap 적음
    • (surface에 가까운) point \(p\) 와 가장 가까운 Gaussian \(g^{\ast}\) 가 다른 Gaussians보다 \(p\) 의 density에 훨씬 많이 기여
      \(g^{\ast} = \text{argmin}_{g}(p - \mu_{g})^T \Sigma_{g}^{-1}(p - \mu_{g})\)

• surface 근처의 점 sampling :
  • assumption :
    거의 surface 위에 있다고 볼 수 있을 정도로 아주 가까운
    surface 근처의 \(p\) 를 Gaussian들의 곱 분포로 sampling
    \(p \sim \prod_{g} N(\cdot; \mu_{g}, \Sigma{g})\)
    • ‘3DGS가 잘 학습됐다면’ small Gaussians는 surface에 아주 가까운 점들의 확률처럼 생각할 수 있고,
      Gaussian이 작을수록 sampling이 중심에 집중되므로
      그 small Gaussians의 곱이 나타내는 분포는 surface 근처의 좁은 영역에 집중된 분포를 나타낼 것이고,
      이로부터 sampling한 점 \(p\) 는 실제 object surface에 가까울 확률이 높다는 가정
    • 이렇게 sampling한 points는 regularization term에 대해 high gradient를 가지는 부분임
• density function :
  • \(d(p) = \sum_{g} \alpha_{g} \text{exp}(-\frac{1}{2}(p - \mu_{g})^T \Sigma_{g}^{-1}(p - \mu_{g}))\)
    where \(\text{exp}(-\frac{1}{2}(p - \mu_{g})^T \Sigma_{g}^{-1}(p - \mu_{g}))\) : posterior
    (점 \(p\) 에 더 가까운 Gaussian의 \(\alpha_{g}\) 가 \(p\) 의 density에 더 많이 기여)
    where \((p - \mu_{g})^T \Sigma_{g}^{-1}(p - \mu_{g})\) : Mahalanobis distance
    (\(p\) 가 Gaussian distribution 평균 \(\mu_{g}\) 에서 “상대적으로” 얼마나 떨어져 있는지)
    (\(p\) 가 평균으로부터 같은 거리만큼 떨어져있더라도 convariance가 작은 방향에 있을수록 Mahalanobis distance가 커짐)
  • approx. ideal density function \(\bar d(p) \in [0, 1]\) :
    • 가정 1) well-distributed Gaussians by regularization term 이므로
      overlap 없다는 전제 하에 하나의 Gaussian \(g^{\ast}\) 가 point \(p\) 의 density 결정
    • 가정 2) Gaussians가 진짜 surface를 묘사하려면 semi-transparent하지 않아야 좋음
      \(\rightarrow\) \(a_{g} = 1\) for any Gaussians
    • 위의 가정과 아래 수식 유도(Approximation of Density function) 에 따르면
      \((p - \mu_{g})^T \Sigma_{g}^{-1}(p - \mu_{g}) \approx \frac{1}{s_{g}^2} \langle p-\mu_{g}, n_g \rangle^{2}\) 이고
      근사해서 구한 ideal density function은
      \(\bar d(p) = \text{exp}(-\frac{1}{2s_{g^{\ast}}^2} \langle p-\mu_{g^{\ast}}, n_{g^{\ast}} \rangle^{2})\)
      where \(g^{\ast} = \text{argmin}_{g}(p - \mu_{g})^T \Sigma_{g}^{-1}(p - \mu_{g})\)

• Regularization on density :
  • \[R = | d(p) - \bar d(p) |\]
    • \(d\) : density function
    • \(\bar d\) : approx. ideal density function
      where 하나의 불투명한 Gaussian이 point density 결정
  • 근데 density function \(d\) 로 regularize하면 아래의 문제가 있다
    • \(d\) 는 exponential term으로 이루어져 있으므로 scale이 너무 커서 optimization에 별로다
    • approx. ideal density function을 구할 때 flat Gaussian으로 surface를 나타내는 게 목적이라고 가정하였는데,
      Gaussian이 완전히 flat 하면 \(s_{g} = 0\) 이 되어 \(\bar d(p) \rightarrow 0\) 이므로
      모든 level set (표면)이 \(\mu_{g}\) 를 지나고 normal \(n_{g}\) 를 가지는 2D 상의 plane이 되어
      level sets 고려하는 게 무의미해진다
      따라서 surface를 나타내기 위해 flat하게 Gaussian을 만드는 게 목적이지만
      그렇다고 완전히 flat하면 안 됨
• Regularization on SDF :
  • density function 말고 SDF로 loss 만들면 optimization 더 잘 됨
    (Gaussians가 surface에 더 잘 align됨)
    \(R = \frac{1}{| P |} \sum_{p \in P} | \hat f(p) - f(p) |\)
    • \(f(p) = \langle p-\mu_{g^{\ast}}, n_{g^{\ast}} \rangle = \pm s_{g^{\ast}} \sqrt{-2log(\bar d(p))}\) :
      ideal distance (SDF) b.w. point \(p\) and true surface
      (\(\bar d(p) = 1\) 이면, 즉 SDF \(f(p) = 0\) (zero level-set)이면, true surface를 나타냄)
    • \(\hat f(p)\) :
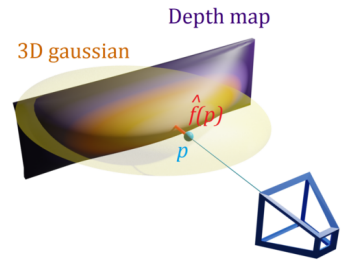
      estimated distance b.w. point \(p\) and depth at projection of \(p\)
      (\(f(p)\) 를 직접 계산하는 건 빡세므로 training view-points에 대해 Radix Sort로 Gaussian rasterize할 때 사용한 Gaussian depth 값들을 rendering하여 depth map을 만들어서 estimated \(\hat f(p)\) 구함)
• Regularization on normal vector :
  • normal vector의 방향 \(n_{g}\) 을 SDF gradient 방향으로 맞춰주기 위해
    (normal vector 방향을 잘 잡아줘야 surface에 잘 align됨)
    \(R_{Norm} = \frac{1}{| P |} \sum_{p \in P} \| \frac{\nabla f(p)}{\| \nabla f(p) \|} - n_{g^{\ast}} \|^2\)

Approximation of Density function

• density function이 실제 surface를 잘 나타낸다면
  \(p\) 에 가장 기여가 큰 Gaussian이 surface에 align되어 flat해야 한다
  이 때, flat Gaussian의 경우 Mahalanobis distance의 주 요인은 covariance의 가장 짧은 축 \(s_{g}\) 이므로
  아래와 같이 approx. ideal density function 식을 유도할 수 있다

• \(\bar d(p) = \text{exp}(-\frac{1}{2s_{g^{\ast}}^2} \langle p-\mu_{g^{\ast}}, n_{g^{\ast}} \rangle^{2})\) 유도 TBD ????
  Eigendecomposition을 하면 \(\Sigma_{g} = Q \Lambda Q^T\)
  where \(s_g\) : convariance가 가장 작은 방향의 vector
  where \(n_g = \frac{s_g}{\| s_g \|}\)

Mesh reconstruction

Obtain Mesh

• 문제 :
  Densification을 거치면 3DGS 수가 너무 많아지고 너무 작아져서
  texture나 detail을 나타내기 힘듦
  \(\rightarrow\) 거의 모든 곳에서 density function \(d = 0\) 이고,
  위에서 언급했듯이 level sets 고려하는 게 의미가 없어져서
  Marching Cubes 기법으로 이러한 sparse density function의 level sets를 추출하기 어렵

• 해결 :

  • 과정 1)
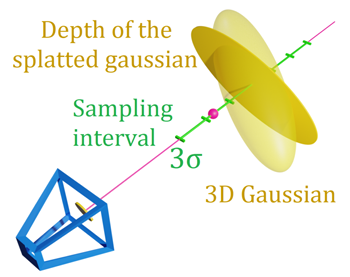
    Gaussians로 계산한 density function level set 상의 visible part에 대해 3D point sampling
    \(n\) 개의 3D points \(\{ p + t_i v_i \}_{i=1}^n\) sampling
    where \(p\) : depth map에 따른 3D point
    where \(t_i \in [-3 \sigma_{g}(v), 3\sigma_{g}(v)]\) (visible part)
    where \(v_i\) : ray direction
  • 과정 2)
    \(d_i = d(p + t_i v_i) = \sum_{g} \alpha_{g} \text{exp}(-\frac{1}{2}((p + t_i v_i) - \mu_{g})^T \Sigma_{g}^{-1}((p + t_i v_i) - \mu_{g}))\) 로
    density 계산한 뒤 level parameter \(\lambda\) 에 대해
    \(d_i \lt \lambda \lt d_j\) 이면,
    range \([d_i, d_j]\) 안에 level set point 있다고 판단
    (아! 그 범위 안에 표면 위의 점이 있구나!)
  • 과정 3)
    해당 level set points와 normals (oriented 3d point clouds \(\vec V\))를 이용하여
    Poisson reconstruction으로 surface mesh 얻음
    (아래에서 설명)

Mesh by Poisson Reconstruction

• Poisson surface reconstruction :
  3D Point Clouds를 3D Mesh로 변환하는 고전적인 방법 (출처 : Link)

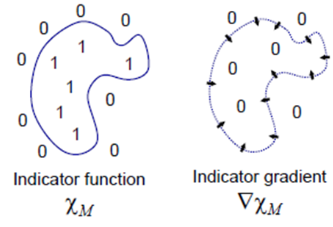
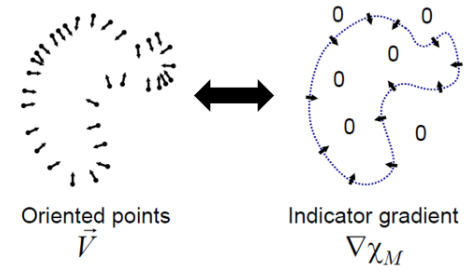
• Let indicator function \(\chi_{M}(p) = \begin{cases} 1 & \text{if} & p \in M \\ 0 & \text{if} & p \notin M \end{cases}\)
  where \(M\) : object mesh 내부

• 주어진 oriented 3d point clouds \(\vec V\) 를 approx.하는 indicator gradient \(\nabla \chi\) 를 찾아야 한다
  이를 풀기 위해 Possion Equation을 사용하자
  • Possion Equation :
    \(\nabla^{2} \phi = f\)
    where \(\nabla = (\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z})\)
    \(\rightarrow\)
    \((\frac{\partial^{2}}{\partial x^2}+\frac{\partial^{2}}{\partial y^2}+\frac{\partial^{2}}{\partial z^2}) \phi (x, y, z) = f(x, y, z)\)
    여기서 scalar field \(f\) 가 주어지면,
    scalar field \(\phi\) 를 찾을 수 있다
  • \(\nabla \chi \approx \vec V\) 원하는 상황인데
    양변에 divergence를 취하면
    \(\nabla \cdot \nabla \chi = \nabla \cdot \vec V\) 은 Poisson Equation 꼴이므로
    \(\nabla \cdot \vec V\) 를 알면 \(\chi\) 를 알 수 있다

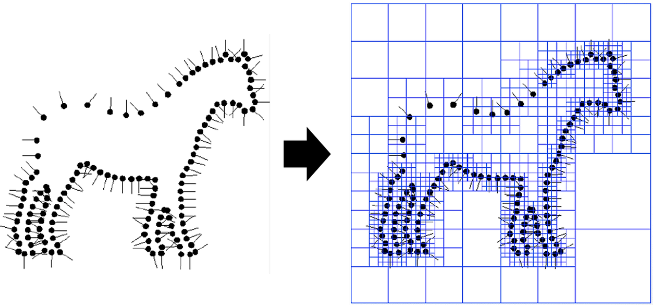
• Implementation :
  • oriented 3d point clouds가 주어지면
    모든 points를 포함하는 큰 육면체를 만들고
    이를 Octree (육면체를 8등분하는 tree)를 사용하여 분할 (Fig 1.)
  • input point clouds \(\vec V\) 는 주변 octree들의 합으로 설계하고,
    octree node의 depth는 Gaussian의 variance로 설계하여
    input point clouds 근처의 octreee들을 Gaussian으로 표현하면
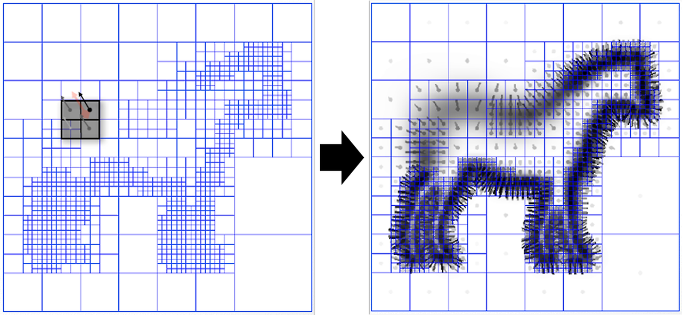
    vector field \(\vec V\) (Fig 2.) 를 얻을 수 있다
  • 각 차원을 편미분 (Divergence)하면 scalar field \(\nabla \cdot \vec V\) (Fig 3.)를 얻을 수 있고,
    Poisson equation \(\nabla \cdot \nabla \chi = \nabla \cdot \vec V\) 에 의해
    indicator function \(\chi\) 도 알 수 있다
    octree의 깊이 별로 각 node의 \(\nabla \vec V\) 값 (Fig 3.)과 \(\nabla \nabla \chi\) 값 (Fig 4.)의 차이를 최소화함으로써 indicator function \(\chi\) 를 구한다
  • mesh화 : input point clouds를 indicator function \(\chi\) 의 입력으로 넣어서 나온 결과값들을 평균 내고, 이 값과 같은 값을 출력하는 좌표들을 surface로 간주 (Fig 5.)하여 Marching Cube 알고리즘으로 mesh 생성
    (Octree Node마다 Marching Cube Polygon 생성)
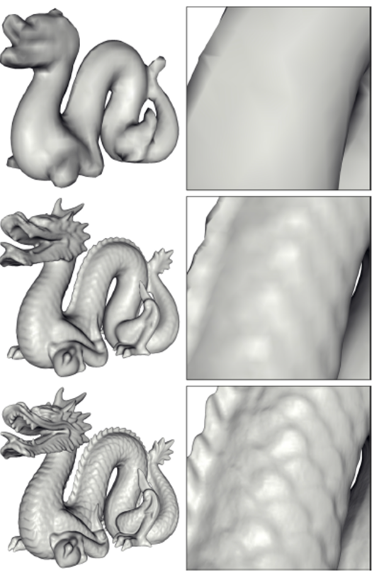
    (여러 fine Octree Node가 하나의 coarse Octree Node를 공유할 때 생기는 문제를 해결하기 위해 fine Octree Node 면의 부분을 coarse한 면으로 projection하는 방법 사용)
  • octree 깊이가 깊어질수록 시간과 memory를 많이 잡아먹긴 하지만, recon.하는 mesh 수가 더 많아서 mesh fine detail을 살릴 수 있음 (Fig 6.)

Fig 1.

Fig 2. vector field (oriented point clouds)

Fig 3. scalar field (divergence of oriented point clouds)

Fig 4. scalar field (laplacian of indicator function)

Fig 5. surface mesh

Fig 6. octree 깊이에 따른 mesh recon. 비교

Refine Mesh

Refine Mesh by Gaussians

• 문제 :
  Poisson reconstruction으로 구한 mesh만 사용하면 rendering quality가 좋지 않음

• 해결 :
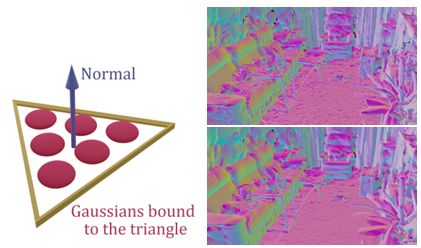
  새로 sampling한 new Gaussians를 (triangle) mesh에 binding하고,
  해당 Gaussians과 mesh를 GS rasterizer로 함께 optimize

  • 과정 1)
    mesh surface 상에서 triangle 당 \(n\) 개의 new thin 3D Gaussians를 sampling하여
    Gaussians를 triangle에 bind
  • 과정 2)
    mesh vertices in barycentric coordinate (무게중심 좌표계) 이용해서
    각 Gaussian의 mean을 explicitly 계산할 수 있음
    (barycentric coordinate : 삼각형 내부의 점을 세 꼭짓점의 가중치로 표현)
  • 과정 3)
    Gaussians를 mesh triangle에 aligned되도록 flat하게 유지하기 위해
    each Gaussian은 2개의 learnable scaling factor \(s_x, s_y\) 와 1개의 learnable 2D quaternion \(q=a+bi\) 을 가지고 있음
    (Gaussians optimize하여 mesh optimze될 때 new thin Gaussians도 함께 optimize)

Code Flow

출처 : NeRF and 3DGS Study

Question

• Q1 : well-distributed 가정을 따르는 approx. ideal density function을 직접 구해서 이를 density function과 비교하는데, GT 역할을 하는 approx. ideal density function이, 변하는 learnable Gaussian으로 구한 것이어도 학습이 안정적임?
• A1 : TBD