pixelSplat

3D Gaussian Splats from Image Pairs for Scalable Generalizable 3D Reconstruction (CVPR 2024)

pixelSplat - 3D Gaussian Splats from Image Pairs for Scalable Generalizable 3D Reconstruction (CVPR 2024)

David Charatan, Sizhe Li, Andrea Tagliasacchi, Vincent Sitzmann

paper :
https://arxiv.org/abs/2312.12337
project website :
https://davidcharatan.com/pixelsplat/
code :
https://github.com/dcharatan/pixelsplat
reference :
NeRF and 3DGS Study

Abstract

• pixelSplat :
  reconstruct a 3DGS primitive-based parameterization of 3D radiance field from only two images

Introduction

• Problem :
  • scale ambiguity :
    camera pose has arbitrary scale factor
  • local minima :
    primitive param.을 random initialization으로부터 직접 optimize하면 local minima 문제 발생
• Contribution :
  • two-view image encoder :
    two-view Epipolar Sampling, Epipolar Attention 덕분에
    scale ambiguity 문제 극복
  • pixel-aligned Gaussian param. prediction module :
    depth를 sampling하기 때문에
    local minima 문제 극복
• Solution :
  • feed-forward model 이, a pair of images로부터,
    3DGS primitives로 parameterized되는 3D radiance field recon.을 학습
• model :
  • per-scene model :
    각각의 scene을 학습하기 위해 정해진 하나의 points set을 iteratively update
    \(\rightarrow\)
    local minima 등 문제 있어서
    3DGS에서는 non-differentiable Adaptive Density Control 기법으로 해결하려 하지만
    이는 일반화 불가능
  • feed-forward model :
    scene마다 얻은 points set을 한 번에 feed-forward로 넣어서 학습
    differentiable하게 일반화 가능
    • attention
    • MASt3R(-SfM), Spann3R, Splatt3R, DUSt3R (잘 모름. 더 서치해봐야 함.)

Background

• local minima :
  • 언제 발생? :
    random location에 initialize된 Gaussian primitives가
    최종 목적지까지 a few std보다 더 많이 움직여야 될 때
    gradient가 vanish 되어버려서
    또는
    최종 목적지까지 loss가 monotonically decrease하지 않을 때
    local minima 발생
  • 해결법? :
    3DGS에서는
    non-differentiable pruning and splitting 기법인
    Adaptive Density Control을 사용하지만
    본 논문에서는
    differentiable parameterization of Gaussian primitives 소개

Scale Ambiguity

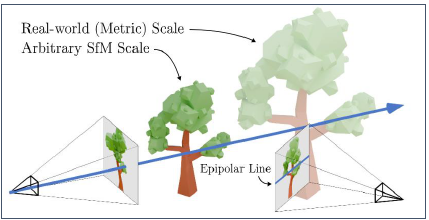
• Scale Ambiguity 문제 :
  • SfM 단계에서 camera pose를 계산할 때
    real-world-scale pose \(T_{j}^{m}\) 을
    metric pose \(s_{i} T_{j}^{m}\) 으로 scale하여 사용
    • \(s_{i}\) :
      arbitrary scale factor
    • metric pose \(s_{i} T_{j}^{m}\) :
      real-world-scale pose의 translation component를 \(s_{i}\) 만큼 scale
  • single image의 camera pose \(s_{i} T_{j}^{m}\) 로부터
    arbitrary scale factor \(s_{i}\) 를 복원하는 건 불가능
• Scale Ambiguity 해결 :
  • two-view encoder에서 a pair of images 로부터
    arbitrary scale factor \(s_{i}\) 복원

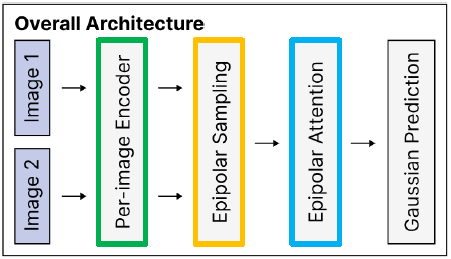
• Two-view encoder Overview :
  • Step 1) Per-Image Encoder
  • Step 2) Epipolar Sampling
  • Step 3) Epipolar Attention

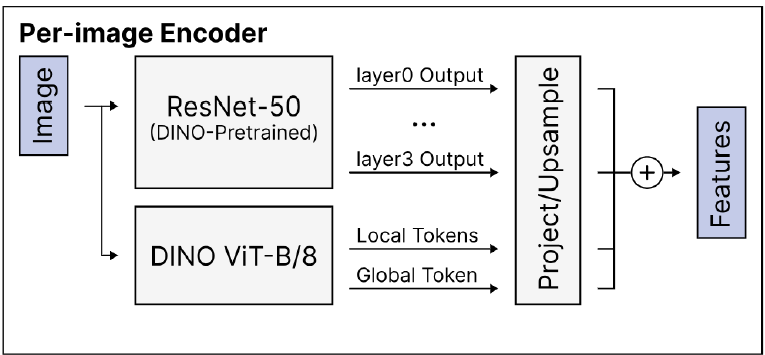
Step 1) Per-Image Encoder

• Step 1) Per-Image Encoder :
  each view (two images)를 각각 feature \(F\), \(\tilde F\) 로 encode

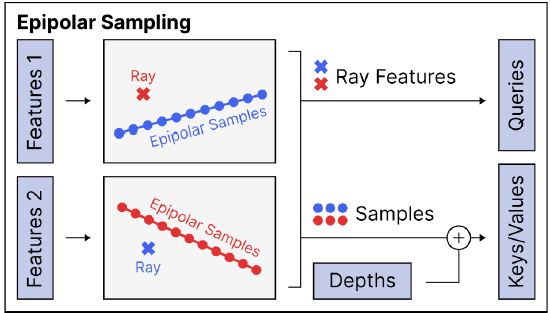
Step 2) Epipolar Sampling

• Step 2) Epipolar Sampling :
  Features 1 from Image 1의 ray로 query 만들고,
  Features 2 from Image 2의 epipolar samples 및 depth 로 key, value 만들어서,
  attention으로 depth scale을 잘 학습하는 게 목적
  (attention : depth 정보와 함께, Image 1의 ray가 Image 2의 epipolar line 위 어떤 sample에 더 많이 attention하는지)
  (epipolar line은 학습하는 게 아니라 수학 식으로 계산)
  • Query :
    \(q = Q \cdot F [u]\)
    where \(F\) : Features 1 from Image 1
    where \(F [u]\) : ray feature at each pixel (in pixel coordinate)
  • Key, Value :
    \(s = \tilde F [\tilde u_{l}] \oplus \gamma (\tilde d_{\tilde u_{l}})\)
    where \(\tilde F\) : Features 2 from Image 2
    where \(\tilde F [\tilde u_{l}]\) : samples on epipolar line
    where \(\tilde d_{\tilde u_{l}}\) : Image 2의 camera 원점까지의 거리
    • \[k_{l} = K \cdot s\]
    • \[v_{l} = V \cdot s\]

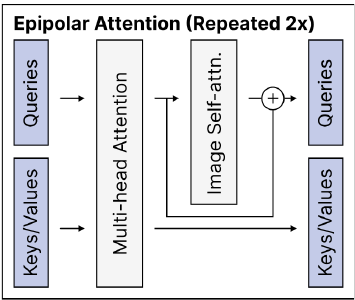
Step 3) Epipolar Attention 중 Epipolar Cross-Attention

• Step 3) Epipolar Attention :
  • Epipolar Cross-Attention :
    앞서 만든 \(q, k_{l}, v_{l}\) 로 cross-attention 수행하여
    per-pixel correpondence b.w. ray and epipolar sample 찾음으로써
    per-pixel feature \(F [u]\) 가 이제
    arbitrary scale factor \(s\) 에 consistent한
    scaled depth를 encode하도록 update
    • \(F [u] += Att(q, k_{l}, v_{l})\)
      where \(+=\) : skip-connection
      where \(Att\) : softmax attention
  • Per-Image Self-Attention :
    Cross-Attention 끝난 뒤 마지막에 Per-Image Self-Attention 수행하여
    propagate scaled depth estimates
    to parts of the image feature maps
    that may not have any epipolar correspondences
    • \[F += SelfAttention(F)\]

Gaussian Parameter Prediction

• 앞선 과정들 덕분에
  scale-aware feature map \(F, \tilde F\) 를 이용하여
  Gaussian param. \(g_{k} = (\mu_{k}, \Sigma_{k}, \alpha_{k}, S_{k})\) 를 예측
  • 2D image 상의 모든 각 pixel은 3D 상의 point에 대응되어
    최종적인 Gaussian primitives set은
    just union of each image
• 3D position Prediction :
  • 방법 1) Baseline :
    predict point estimate of 3D position \(\mu\)
    • \(\boldsymbol \mu = \boldsymbol o + d_{u} \boldsymbol d\)
      where \(u\) : 2D pixel coordiante
      where \(\boldsymbol d = R K^{-1} [u, 1]^{T}\) : ray direction
      where \(d_{u} = g_{\theta}(F [u])\) : depth obtained by neural network
    • 문제 :
      depth 자체를 neural network로 추정하는 건 local minima 문제 발생하기 쉬움
  • 방법 2) 본 논문 방식 :
    predict probability density of 3D position \(\mu\)
    • 핵심 :
      neural network로
      depth 자체를 예측하는 게 아니라
      differentiable probability distribution of likelihood of depth along ray를 예측
    • Step 1)
      depth를 \(Z\)-bins로 discretize
      \(b_{z} = ((1 - \frac{z}{Z})(\frac{1}{d_{near}} - \frac{1}{d_{far}}) + \frac{1}{d_{far}})^{-1} \in [d_{near}, d_{far}]\)
      for \(z \in [0, Z]\) : depth index
    • Step 2)
      discrete probability \(\phi\) 로부터 index \(z\) 를 sampling
      \(z \sim p_{\phi}(z)\)
    • Step 3)
      ray를 쏴서(unproject) Gaussian mean \(\mu\) 계산
      \(\boldsymbol \mu = \boldsymbol o + (b_{z} + \delta_{z}) \boldsymbol d\)
      where \(\phi\) : depth(\(z\)) probability obtained by neural network
      where \(\delta_{z}\) : depth offset obtained by neural network

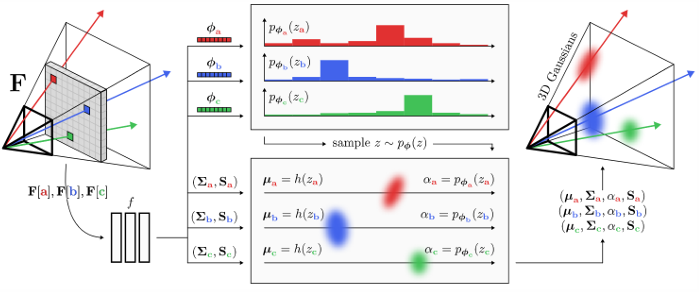
• Gaussian Parameter Prediction :
  • scale-aware feature map \(F, \tilde F\) 과 neural network \(f\) 를 이용하여
    \(\phi, \delta, \Sigma, S = f(F [u])\)
    where \(\phi, \delta, \Sigma, S\) : depth probability, depth offset, covariance, spherical harmonics coeff.
    • 3D position(mean) :
      \(\phi, \delta\) 이용해서
      \(\boldsymbol \mu = \boldsymbol o + (b_{z} + \delta_{z}) \boldsymbol d\)
    • Covariance :
      \(\Sigma\)
    • Spherical Harmonics Coeff. :
      \(S\)
    • Opacity :
      \(\phi\) 이용해서
      \(\alpha = \phi_{z}\)
      \(=\) probability of sampled depth \(z\)
      (so that we make sampling differentiable)
  • 각 pixel마다 3DGS point에 대응되므로
    pixel-aligned Gaussians라고 부름

Experiments

• Setup :
  • Dataset :
    camera pose is computed by SfM
    • RealEstate 10k
    • ACID
  • Baseline :
    • pixelNeRF
    • GPNR
    • Method of Du et al.
  • Metric :
    • PSNR
    • SSIM
    • LPIPS

• Result :
  • performance much better
  • inference time faster
  • less memory per ray

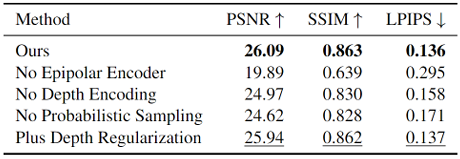
Ablation Study

• Ablation Study :
  • Epipolar Encoder : Epipolar Sampling and Epipolar Attention
  • Depth Encoding : freq.-based positional encoding \(\gamma(\tilde d_{\tilde u_{l}})\)
  • Probabilistic Sampling : depth index \(z \sim p_{\phi}(z)\)
  • Depth Regularization : ???