7DGS (6DGS)

Unified Spatial-Temporal-Angular Gaussian Splatting

7DGS - Unified Spatial-Temporal-Angular Gaussian Splatting

Zhongpai Gao, Benjamin Planche, Meng Zheng, Anwesa Choudhuri, Terrence Chen, Ziyan Wu

paper :
https://arxiv.org/abs/2503.07946
project website :
https://gaozhongpai.github.io/7dgs/

핵심 요약 :

1. 7D = 3D spatial + 3D directional + 1D temporal
2. 고정된 covariance를 가진 납작한 anisotropic 3DGS는 view-dependent effect에 취약함.
   근데 7DGS는 각기 다른 \(t, d\) 에 맞춰서 학습되었기 때문에 (customized 느낌) view-dependent and dynamic 잘 표현 가능
3. Adaptive Gaussian Refinement : \(t, d\) 에 따라 7DGS의 param.(spatial, temporal, directional mean and covariance)를 MLP로 변형시킴.
4. Slice : 3DGS의 기존 framework를 그대로 사용하기 위해 rendering \(t, d\) 에 대해 7DGS를 3DGS로 slice하는데,
   covariance는 미리 계산해둘 수 있고 spatial mean과 opacity는 rendering할 때마다 \(t, d\) 에 따라 달라짐.
   7DGS를 3DGS로 slice할 때 \(t, d\) 가 mean \(\mu_{t}, \mu_{d}\) 에서 멀수록 spatial mean \(\mu_{p}\) 을 많이 변형시킴.

Direction-Aware 6DGS

• Abstract :
  • 3DGS와 N-dimensional Gaussian (N-DG) 을 결합하여
    direction 정보도 param.에 반영함으로써
    non-planar geometry, parallax effects, view-dependent effects를 효과적으로 모델링
  • learnable param.만 달라졌을 뿐
    특정 direction에 대해 6DGS를 3DGS로 slice하면 기존 3DGS framework와 동일하게 작동

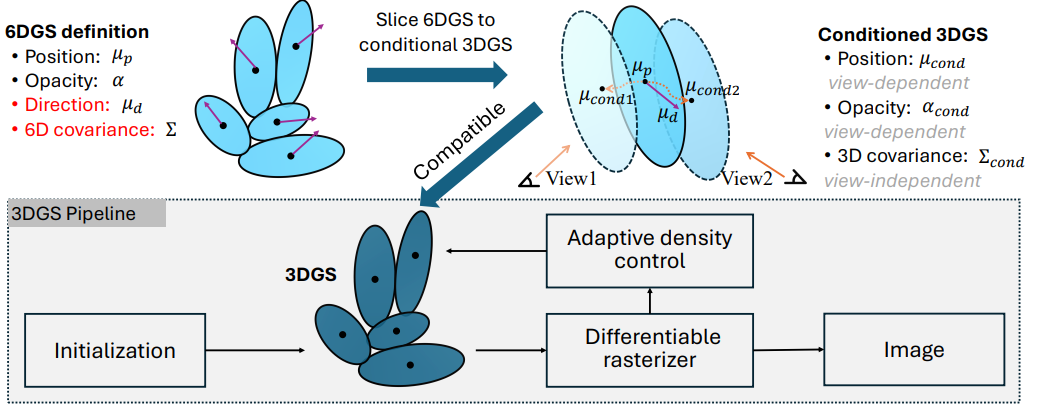
• Parameter :
  • 기존 3DGS param. :
    • mean
    • covariance (quaternion, scale)
    • opacity
    • SH coeff.
  • 6DGS param. :
    3D position (공간) 정보 뿐만 아니라 3D direction (방향) 정보도 param.에 담음!
    그래서 이제 color 뿐만 아니라 position, covariance, opacity도 모두 view-dependent!
    • position mean \(\in R^{3}\)
    • direction mean \(\in R^{3}\)
    • covariance matrix \(\Sigma = L L^{T} \in R^{6 \times 6}\)
      for lower triangular matrix \(L\)
      • diagonal elements : positive by exponential activation
      • off-diagonal elements : \(\in [-1, 1]\) by sigmoid activation
    • opacity \(\in R^{1}\)
    • color \(\in R^{3}\)
  • Slice 6DGS into conditional 3DGS :
    공간, 방향 정보를 갖고 있는 6DGS에 대해
    특정 방향이 정해지면
    조건부 분포를 통해 해당 방향에서의 3DGS로 slice할 수 있음

Slice 6DGS into conditional 3DGS

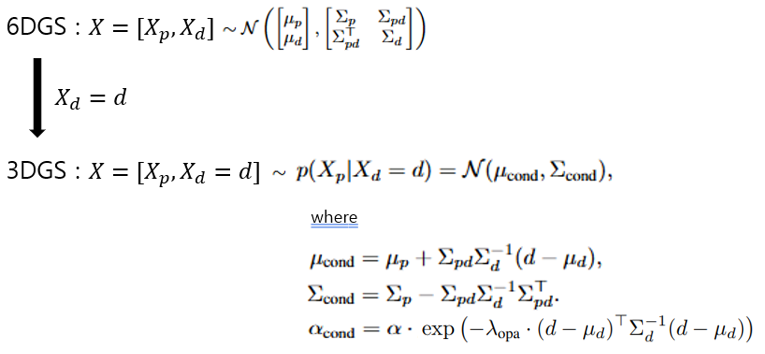
• Conditional Gaussian :
  • Conditional Mean \(\mu_{cond}\) :
    Best Linear Unbiased Estimator for
    position mean, adjusting dynamically based on the viewing direction
    • rendering할 때마다 view direction \(d\) 로 계산해야 함
  • Conditional Covariance \(\Sigma_{cond}\) :
    joint covariance \(\Sigma\) 에서 \(X_{d}\) 와의 correlation에 해당하는 부분을 제거하고 남은 residual uncertainty in \(X_{p}\)
    • rendering 이전에 미리 계산해놓을 수 있음
  • Conditional Opacity \(\alpha_{cond}\) :
    opacity \(\alpha\) 를 direction의 PDF로 attenuate하여
    view-dependent opacity 반영
    (각도에 따라 opacity도 달라짐!)
    • rendering할 때마다 view direction \(d\) 로 계산해야 함
    • \(0 \lt \lambda_{opa} \lt 1\) : view-direction이 opacity에 얼마나 영향을 미칠 건지 (hyper-param. 또는 per-Gaussian learnable param.)
• Adaptive Control :
  • 기존 3DGS에서처럼 Adaptive Density Control (cloning, splitting) 할 때만 \(R, S\) 필요한데,
    6DGS의 covariance \(\Sigma = LL^{T}\) 에서는 바로 얻을 수 없으므로
    \(\Sigma_{cond} = UDU^{T}\) 로 분해 (SVD)해서 \(R, S\) 얻음
    • \(R = U\) and \(S = \sqrt{\text{diag}(D)}\) 이 때, \(R\) 이 right-handed coord.를 따르도록 하기 위해
      last column (z축)의 부호 조정
      \(R_{:, 3} = R_{:, 3} \cdot \text{sign}(\text{det}(R))\)
  • opacity \(\alpha\) 값이 threshold보다 작거나, 크기가 매우 크면 prune

Spatial-Temporal-Angular 7DGS

• 7DGS param. :
  • position mean \(\mu_{p} \in R^{3}\)
  • temporal mean \(\mu_{t} \in R^{1}\)
  • directional mean \(\mu_{d} \in R^{3}\)
  • covariance matrix \(\Sigma = L L^{T} \in R^{7 \times 7}\)
    for lower triangular matrix \(L\)
  • opacity \(\in R^{1}\)
  • color \(\in R^{3}\)

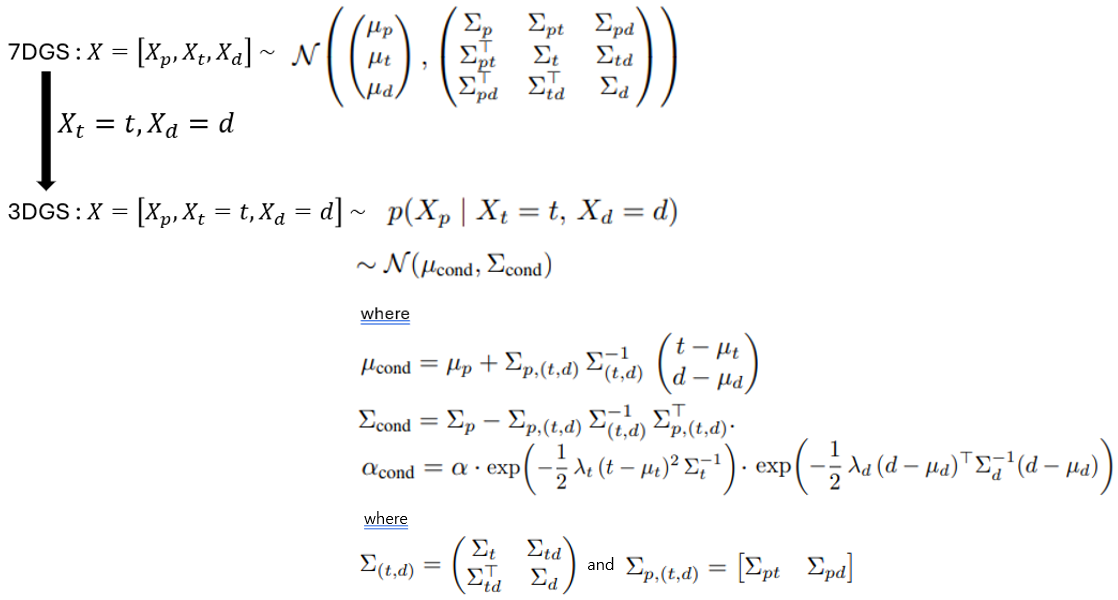
• Slice 7DGS into conditional 3DGS :
  공간, 방향, 시간 정보를 갖고 있는 7DGS에 대해
  특정 방향, 시간이 정해지면
  조건부 분포를 통해 해당 방향, 시간에서의 3DGS로 slice할 수 있음
  • Conditional Mean \(\mu_{cond}\) :
    • rendering할 때마다의 time \(t\), view-direction \(d\) 로 계산해야 함
  • Conditional Covariance \(\Sigma_{cond}\) :
    temporal, directional variance를 제거하고 남은 residual uncertainty in \(X_{p}\)
    • rendering 이전에 미리 계산해놓을 수 있음
  • Conditional Opacity \(\alpha_{cond}\) :
    opacity \(\alpha\) 를 direction의 PDF와 temporal PDF로 attenuate
    (각도와 시간에 따라 opacity도 달라짐!)
    • rendering할 때마다의 time \(t\), view-direction \(d\) 로 계산해야 함
    • positive \(\lambda_{t}, \lambda_{d}\) : time, view-direction이 얼마나 영향 미칠 건지
    • 만약 rendering하려는 current time \(t\) 와 view-direction \(d\) 가 평균값에서 멀다면
      해당 Gaussian은 rendering에 덜 기여
  • 그렇게 구한 conditional \(\mu_{cond}, \Sigma_{cond}, \alpha_{cond}\) 를 기존 3DGS framework에 그대로 적용
• Adaptive Gaussian Refinement :
  • 시간 \(t\) 가 지남에 따라
    sliced 3DGS의 spatial mean \(\mu_{cond}\) 과 opacity \(\alpha_{cond}\) 는 dynamically 변하지만
    sliced 3DGS의 shape (covariance) \(\Sigma_{cond}\) 는 static 이므로 complex dynamic behavior 표현에 방해될 수 있음
  • Adaptive Gaussian Refinement :
    가벼운 MLP로 7DGS param.를 dynamically update
    • feature \(f = \text{concat}[\mu_{p}, \mu_{t}, \mu_{d}, \gamma(t)]\)
    • Refine Gaussian param. by two-layer MLP \(\phi\) :
      그럼 이제 (slice하기 전) 7DGS의 spatial, temporal, directional mean과 covariance가 dynamically 시간에 따라 변하는 값!
      • mean :
        \(\hat \mu_{p} = \mu_{p} + \phi_{p} (f)\) and
        \(\hat \mu_{t} = \mu_{t} + \phi_{t} (f)\) and
        \(\hat \mu_{d} = \mu_{d} + \phi_{d} (f)\) and
      • covariance :
        \(\hat l = l + \phi_{l} (f)\)
        where \(l\) is vectorized lower-triangular elements of \(L\)

• Optimization and Rendering Pipeline :
  • Adaptive Control :
    • 기존 3DGS에서처럼 Adaptive Density Control (cloning, splitting) 할 때만 \(R, S\) 필요한데,
      7DGS의 covariance \(\Sigma = LL^{T}\) 에서는 바로 얻을 수 없으므로
      sliced 3DGS의 covariance를 \(\Sigma_{cond} = UDU^{T}\) 로 분해 (SVD)해서 \(R, S\) 얻음
      • \(R = U\) and \(S = \sqrt{\text{diag}(D)}\) 이 때, \(R\) 이 right-handed coord.를 따르도록 하기 위해
        last column (z축)의 부호 조정
        \(R_{:, 3} = R_{:, 3} \cdot \text{sign}(\text{det}(R))\) s.t. \(\text{det}(R) \gt 0\)
    • Cloning
    • Splitting :
      \(\Sigma_{pt}\) 의 크기 (spatial-temporal correlation)가 threshold보다 크거나
      \(\Sigma_{t}\) 로부터 유도한 normalized temporal scale이 threshold보다 크면
      Split!
      • 이는 motion dynamic이 큰 (많이 움직이는) 영역에 7DGS가 많이 분포하도록 함
    • Pruning :
      opacity \(\alpha\) 값이 threshold보다 작거나, 크기가 매우 크면 prune
  • Rendering :
    7DGS를 3DGS로 slice하면 기존 3DGS의 framework와 동일하게 작동
    (동일한 loss, optimizer, hyperparam. setting 사용
    except increased \(\alpha\) threshold \(\tau_{min} = 0.01\))
• Results :
  D-NeRF, Technicolor, 7DGS-PBR Dataset에 대해
  훨씬 적은 Gaussian points로도
  PSNR 7.36dB 이상 올리고 400 FPS 이상의 render speed 유지하여 SOTA 달성

Question

• Q1 :
  7DGS를 3DGS로 slice할 때 3D spatial mean \(\mu_{cond}\) 이 \(t, d\) 에 따라 달라지는 것도 합리적인가요?

• A1 :
  고정된 covariance를 가진 납작한 anisotropic 3DGS는 view-dependent effect에 취약함.
  \(t, d\) 가 바뀜에 따라 7DGS의 param.(spatial, temporal, directional mean and covariance)를 Adaptive Gaussian Refinement로 변형시키는 것도 합리적이고,
  7DGS를 3DGS로 slice할 때 \(t, d\) 가 mean \(\mu_{t}, \mu_{d}\) 에 가까울수록 spatial mean \(\mu_{p}\) 을 덜 변형시키는 것도 합리적임.
  (7DGS를 3DGS로 slice할 때 \(t, d\) 가 mean \(\mu_{t}, \mu_{d}\) 에서 멀수록 spatial mean \(\mu_{p}\) 을 많이 변형시키는 것도 합리적임.)
  결국 \(t, d\) 에 따라 mean, covariance가 전부 달라지므로 아예 새로운 Gaussian을 만드는 것과 같은데 학습만 잘 되면 성능 높아질 수 있음.