Dynamic Gaussian Marbles

Dynamic Gaussian Marbles for Novel View Synthesis of Casual Monocular Videos (SIGGRAPH 2024)

Dynamic Gaussian Marbles for Novel View Synthesis of Casual Monocular Videos

Colton Stearns, Adam Harley, Mikaela Uy, Florian Dubost, Federico Tombari, Gordon Wetzstein, Leonidas Guibas

paper :
https://arxiv.org/abs/2406.18717
project website :
https://geometry.stanford.edu/projects/dynamic-gaussian-marbles.github.io/

Contribution

• Dynamic 4D Gaussian Splatting :
  • 이전까지는 multiple simultaneous viewpoints of a scene 세팅 (dense multi-camera setup)에서의 recon. 논문들이 많았음
    \(\rightarrow\)
    평소의 casual monocular video (challenging)로 4D recon.을 수행해보자!
  • input에 multi-view info.가 없는 underconstrained monocular video더라도
    prior (careful optimization strategy 및 off-the-shelf depth and motion estimation 및 geometry-based regularization) 이용해서
    적절한 constraint를 복원할 수 있다!
• Dynamic Gaussian Marbles :
  monocular setting의 어려움을 해결하기 위해 GS에서 세 가지 사항을 변경
  이를 통해 Gaussian trajectories를 학습할 수 있음
  • isotropic Gaussian Marbles :
    isotropic Gaussian을 사용함으로써
    Gaussian의 degrees of freedom을 줄이고
local shape보다는 motion과 apperance 표현하는 데 더 집중하도록 제한
  • hierarchical divide-and-conquer learning strategy :
    time 길이가 어느 정도 짧아야 잘 포착할 수 있으므로
    long video를 short subsequences로 나누고 optimize by iteratively merging the subsequences
    (long-sequence tracking 대신 인접한 subsequences를 붙이는 task로!)
    • procedure :
      아래의 과정을 반복하며 locality와 global coherence를 모두 챙김!
      • motion estimation :
        \(G^{b}\) 의 frame을 \(G^{a}\) 의 trajectory에 하나씩 더해 가며 motion estimation을 수행하므로 [1] 처럼 locality와 smoothness로부터 benefit
      • merge
      • global adjustment : [2] 처럼 global coherence라는 benefit
  • prior :
    monocular video로도 recon. 잘 수행하기 위해 prior 이용
    • image(2D)-space prior : SAM (Rendering loss-segmentation), CoTracker (Tracking loss), DepthAnything (Rendering loss-depthmap)
    • geometry(3D)-space prior : regularization of Gaussian trajectories with rigidity (Isometry loss) and Chamfer priors (3D Alignment loss)

Related Work

• Gaussian Splatting :
  TBD

• Dynamic Gaussian Splatting :
  TBD

• Other Dynamic Nerual Scene Representations :
  TBD

Method

Overview

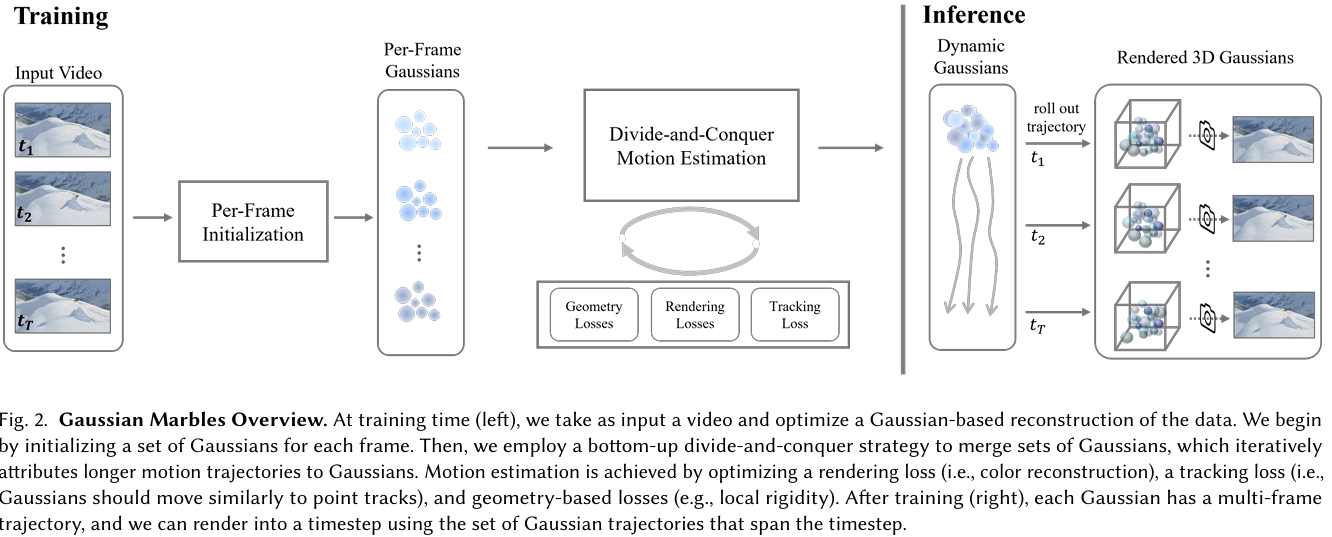
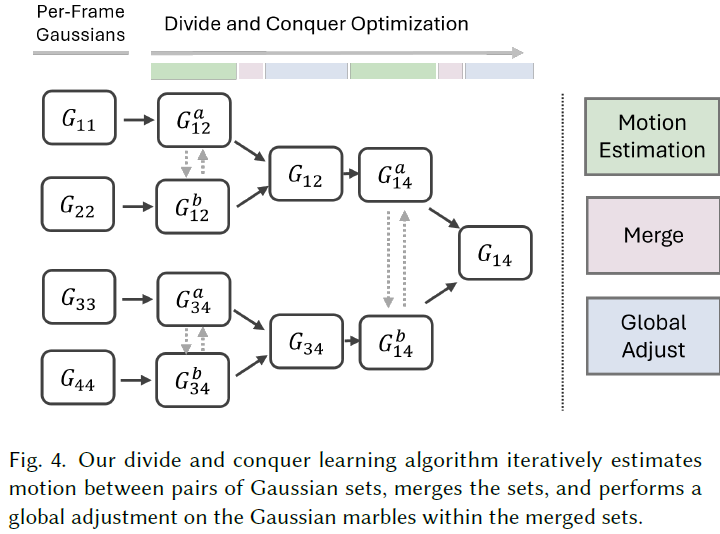
Dynamic Gaussian Marbles

simpler Gaussian Marble의 경우에만 generalize well to novel view

• Gaussian marble :
  • isotropic :
    \(R = I\) and \(S = s \in R^{1}\)
    • anisotropic Gaussian은 expensive할 뿐만 아니라
      underconstrained monocular cam. setting에서는 오히려 degrees of freedom 많으면 poor하다는 걸 실험적으로 발견
  • semantic instance :
    assign each Gaussian marble to semantic instance \(y \in N\) by SAM-driven TrackAnything
  • dynamic trajectory :
    trajectory \(\Delta X \in R^{T \times 3}\) : a sequence of translations which maps marble’s position change at each timestep

Divide-and-Conquer Motion Estimation

• Training Procedure :
  • Step 1) initialization for each frame
    initialize Gaussian marbles \([G_{11}, G_{22}, \ldots, G_{TT}]\) for each frame
    (initial marbles \(G_{ii}\) have trajectory length 1)
    • Step 1-1) obtain prior (depthmap and segmentation)
      obtain monocular (LiDAR) depthmap and segmentation from SAM-driven TrackAnything [3]
    • Step 1-2) unproject from 2D to 3D
      unproject the depthmap into point cloud
      perform outlier removal and downsampling
    • Step 1-3) initialize Gaussian marbles and trajectory
      • Gaussian marbles :
        • mean \(\mu \in R^{3}\) : Step 1-2)에서 얻은 pcd
        • color \(c \in R^{3}\) : pixel color (pixel-aligned Gaussians)
        • instance class \(y \in R^{1}\) : Step 1-1)에서 얻은 segmentation
        • scale \(s \in R^{1}\) and opacity \(\alpha \in R^{1}\) : 3DGS 논문에서 했던대로 초기화
      • trajectory :
        • trajectory : \(\Delta X = [\boldsymbol 0] \in R^{T \times 3}\)
  • Step 2) bottom-up divide-and-conquer merge
    merge short-trajectories into longer trajectories
    e.g. \(G = [G_{12}, G_{34}, G_{56}, G_{78}] \rightarrow G = [G_{14}, G{58}]\)
    • Step 2-1) motion estimation
      • Step 2-1-1) make a pair b.w. adjacent marbles
        • adjacent Gaussian marble set끼리 a pair로 묶음
          e.g. \([(G_{12}^{a}, G_{34}^{b}), (G_{56}^{a}, G_{78}^{b})]\)
        • \(G^{a}\) 는 merge할 prev. frames’ Gaussians이고,
          \(G^{b}\) 는 merge할 next frames’ Gaussians
      • Step 2-1-2) \(G^{a}\) 의 trajectory 확장
        • goal :
          \(G_{12}^{a}\) 의 trajectory인 \(\Delta X = [\Delta X_{1}, \Delta X_{2}]\) 는 이미 학습되어 merge된 motion이고,
          \(G_{12}^{a}\) 의 trajectory와 \(G_{34}^{b}\) 의 frame \(3\) 을 잇는 motion \(\Delta X_{3}\) 을 학습해야 함!
        • constant-velocity assumption에 따라 trajectory를 \(\Delta X = [\Delta X_{1}, \Delta X_{2}, \Delta X_{3}^{init}]\) 로 확장
      • Step 2-1-3) trajectory optimization
        • \(G_{12}^{a}\) 를 frame \(3\) 에 render한 뒤
          \(\Delta X_{3}\) 이 frame \(3\) 으로의 motion을 잘 반영하도록 \(\Delta X_{3}\) 을 업데이트
          (\(\eta\) 번 반복 by 아래에서 설명할 Loss)
      • Step 2-1-4) repeat
        • Step 2-1-2), Step 2-1-3)을 반복
          until \(G^{a}\) 의 trajectory가 \(G_{34}^{b}\) 내 모든 frames를 커버할 때까지
        • e.g. \(G^{a}\) 의 trajectory를 \(\Delta X = [\Delta X_{1}, \Delta X_{2}, \Delta X_{3}, \Delta X_{4}^{init}]\) 로 확장한 뒤
          \(G^{a}\) 를 frame \(4\) 에 render한 뒤
          \(\Delta X_{4}\) 가 frame \(4\) 으로의 motion을 잘 반영하도록 \(\Delta X_{4}\) 을 업데이트
    • Step 2-2) merge
      • motion estimation을 거치고 나면 \(G_{ij}^{a}\) 와 \(G_{ij}^{b}\) 가 같은 frame subsequence \([i, j]\) 를 recon.할 것이므로
        merge by just union \(G_{ij} = G_{ij}^{a} \cup G_{ij}^{b}\)
        (set size 2배 됨)
      • computational load 줄이기 위해
        opacity 또는 scale이 너무 작은 Gaussians는 drop하고,
        random downsampling 수행하여
        set size를 constant하게 유지
    • Step 2-3) global adjustment
      • merge로 합치고 나서도 still optimized라는 보장이 없기 때문에
        newly merged Gaussians를 모두 jointly optimize
      • merged set가 \(G_{ij}\) 라고 했을 때
        \([i, j]\) 내 a frame을 randomly sampling하고
        \(G_{ij}\) 의 모든 Gaussians를 해당 frame에 render한 뒤
        Gaussian \(c, s, \alpha, \Delta X\) 을 업데이트
        (\(\beta\) 번 반복)
      • 그럼 merged Gaussians \(G_{ij}\) 가 global Gaussians로 인정받을 수 있음!
• Inference Procedure :
  • learned Gaussian trajectories 이용해서
    render (roll out) into specific timestep \(t\)

Loss

Motion Estimation 단계에서 아래의 Loss들 사용!

• Tracking Loss :
  \(L_{track} = \sum_{p \in P} \sum_{g \in N(p_{i})} \alpha_{i}^{'} \| D_{i} \| \mu_{i}^{'} - p_{i} \| - D_{j} \| \mu_{j}^{'} - p_{j} \| \|\)
  where \(\mu_{i}^{'}\) and \(D_{i}\) : mean and depth of projected 2D Gaussian
  where \(P\) : tracked points by CoTracker [4]
  where \(N(p_{i})\) : tracked point \(p_{i}\) 와의 the nearest 3D Gaussians
  where \(\alpha_{i}^{'}\) : Gaussian’s opacity
  • goal :
    2D point track인 CoTracker [4] (2D prior)를 사용하여
    Gassian marble trajectories를 regularize
  • Step 1)
    \(G^{b}\) 의 frame \(j\) 로의 \(\Delta X_{j}\) 를 optimize하고자 할 때,
    CoTracker [4] 를 이용하여 frames \([j - w , j + w]\) (\(w = 12\))에서의 point tracks \(P\) 를 estimate
    (from 2D frame to 2D frame)
    (일종의 GT로 사용)
  • Step 2)
    a source frame \(i \in [j - w , j + w]\) 을 randomly sampling
  • Step 3)
    Gaussian marble trajectory \(\Delta X\) 로부터 frame \(i\) 와 frame \(j\) 에서의 3DGS position을 sampling하고
    3DGS를 2D Gaussian in image plane으로 project시켜 2D mean, depth, covariance 구함
  • Step 4)
    Step 1)의 tracked point \(p_{i \rightarrow j}\) 와 가장 가까운 \(K = 32\) 개의 Step 3)의 2D Gaussians를 구한 뒤
    2D tracked point와 2D Gaussian 사이의 거리가 frame \(i\), \(j\) 에서 거의 일정하게 유지되도록 loss term 걸어줌
    (for temporal consistency)
• Rendering Loss :
  • image rendering하여
    GT image와의 L1 loss 및 LPIPS loss 구함
  • disparity map rendering하여
    initial disparity estimation과의 L1 loss 구함
  • segmentation map rendering하여
    SAM(off-the-shelf instance segmentation)과의 L1 loss 구함
• Geometry Loss :
  • Local Isometry Loss :
    \(L_{iso-local} = \sum_{g^{a} \in G} \sum_{g^{b} \in N(g^{a})} | \| \mu_{i}^{a} - \mu_{i}^{b} \| - \| \mu_{j}^{a} - \mu_{j}^{b} \| |\)
    • goal :
      prev. works [2], [5] 에서처럼
      Gaussian marbles가 locally rigid motion을 따르도록 regularize
    • Step 1)
      \(G^{b}\) 의 frame \(j\) 로의 \(\Delta X_{j}\) 를 optimize하고자 할 때,
      우선 a source timestep \(i \in [j - 1 , j + 1]\) 을 randomly sampling
    • Step 2)
      3DGS \(g^{a} \in G\) 및 이와 가까운 3DGS들 \(g^{b} \in N(g^{a})\) 에 대해
      nearest 3D Gaussians끼리의 거리가 frame \(i\), \(j\) 에서 거의 일정하게 유지되도록 loss term 걸어줌
  • Instance Isometry Loss :
    \(L_{iso-instance} = \sum_{g^{a} \in G} \sum_{g^{b} \in Y(g^{a})} | \| \mu_{i}^{a} - \mu_{i}^{b} \| - \| \mu_{j}^{a} - \mu_{j}^{b} \| |\)
    • goal :
      각 semantic instance가 일관적으로 움직이도록 regularize
    • Step 1)
      \(G^{b}\) 의 frame \(j\) 로의 \(\Delta X_{j}\) 를 optimize하고자 할 때,
      우선 a source timestep \(i \in [j - 1 , j + 1]\) 을 randomly sampling
    • Step 2)
      3DGS \(g^{a} \in G\) 및 이와 semantic label이 같은 3DGS들 \(g^{b} \in Y(g^{a})\) 에 대해
      semantic label이 같은 3D Gaussians끼리의 거리가 frame \(i\), \(j\) 에서 거의 일정하게 유지되도록 loss term 걸어줌
  • 3D Alignment Loss :
    \(L_{chamfer} = \sum_{g^{1} \in G^{1}} \text{min}_{g^{2} \in G^{2}} \| \mu^{1} - \mu^{2} \| + \sum_{g^{2} \in G^{2}} \text{min}_{g^{1} \in G^{1}} \| \mu^{1} - \mu^{2} \|\)
    • goal :
      merge하고나서 Global Adjustment할 때 a frame에 전부 rendering해서 optimize하므로 projected 2D image plane 상에서는 align 되어 있음
      그런데 merge하고나서 3D space 상에서도 align할 필요 있음
      (3DGS를 align한다는 게 무슨 의미지? 모든 3DGS가 함께 scene recon.에 기여하도록 서로 가깝게 만든다는 건가 ???)
      (만약에 3D alignment 하지 않으면 3D and novel-view 상에서 cloudy artifacts 생김)
      (off-the-shelf depth estimation이 time에 따라 inconsistent할 경우 이와 같은 상황 발생)
    • Step 1)
      두 pcd 집합을 서로 가깝게 만드는 Chamfer loss를 적용할 건데,
      merge할 Gaussian set \(G^{a}\) 와 \(G^{b}\) 는 scene의 명확히 서로 다른 부분을 관측하고 있으므로
      둘 사이에 Chamfer loss를 바로 적용하면 안 됨
    • Step 2)
      set \(G_{12}^{a}\) 와 \(G_{34}^{b}\) 를 single frame의 subsets \([G_{1}^{a}, G_{2}^{a}, G_{3}^{b}, G_{4}^{b}]\) 로 나눔
      where \(G_{1}^{a}\) contains Gaussians initialized from frame \(1\)
    • Step 3)
      해당 subsets list를 random shuffle한 뒤
      맨 앞의 25%는 set \(G^{1}\) 으로 묶고, 다음 25%는 set \(G^{2}\) 로 묶음
      (\(G^{1}\) 과 \(G^{2}\) 가 scene의 어떤 부분을 보고 있는지 명확히 정해지지 않도록 randomness 부여)
      (만약 이렇게 randomness 부여하지 않는다면 observed scene content difference에 overfitting될 수 있음 ???)
    • Step 4)
      \(G^{1}\) 과 \(G^{2}\) 에 대해 2-way Chamfer distance 계산

Experiment

Dataset

• training :
  아래의 두 가지 datasets는 multi-view info.를 포함하고 있으므로
  monocular setting을 모방하기 위해
  training and evaluation protocol을 수정
  • NVIDIA Dynamic Scenes Dataset :
    • 구성 :
      7 videos
      12 calibrated cameras
    • setting :
      prev. benchmarked evaluations는 각 timestep마다 different training camera를 사용하는데,
      (monocular teleporting camera 방식 [6])
      이는 realistic monocular video setting이 아니므로
      본 논문에서는 single camera 4를 training에 사용하고 single camera 3, 5, 6을 evaluation에 사용
  • DyCheck iPhone Dataset :
    • 구성 :
      7 videos
    • setting :
      single camera로 구성되어 있는 monocular video setting이긴 하지만
      multi-view info.를 포함하도록 3D trajectory가 scene 전체를 돌기 때문에
      camera의 calculated motion은 일상 video와 다르다
      • 방법 1) official benchmark 그대로 사용
      • 방법 2) camera pose 제거
        We remove camera poses, offloading the camera motion into the learned 4D scene representation’s dynamics. We find this setting interesting because it simulates additional dynamic content, where previously “static” regions of the scene now have rigid dynamics equal to the inverse camera motion, which must be solved by the scene representation itself. ???
• test :
  • Total-Recon Dataset :
    2 time-synchronized and calibrated videos with LiDAR
  • Davis Dataset
  • YouTube-VOS Dataset
  • real-world videos

Implementation

• Implementation :
  • NVIDIA Dynamic Scenes Dataset :
    • 120,000 Gaussians per frame and upsample to 240,000 Gaussians during the last stage of global adjustment
    • \(\eta = 128\) on motion estimation and \(\beta = 48\) on global adjustment
    • stop divide-and-conquer after learning subsequences of length 32 on both fg and bg
  • DyCheck iPhone Dataset :
    • 220,000 Gaussians per frame if camear pose exists else 180,000 Gaussians
    • \(\eta = 80\) on motion estimation and \(\beta = 32\) on global adjustment
    • stop divide-and-conquer after learning subsequences of length 8 on fg and length 32(512) on bg
      (when there exists camera pose, need to learn more a dynamic bg)
  • Total-Recon Dataset :
    • 120,000 Gaussians per frame
    • $\eta = 80\(on motion estimation and\)\beta = 32$$ on global adjustment
    • stop divide-and-conquer after learning subsequences of length 8 on fg and length 32 on bg

Results

• Dynamic Novel View Synthesis :
  • TBD

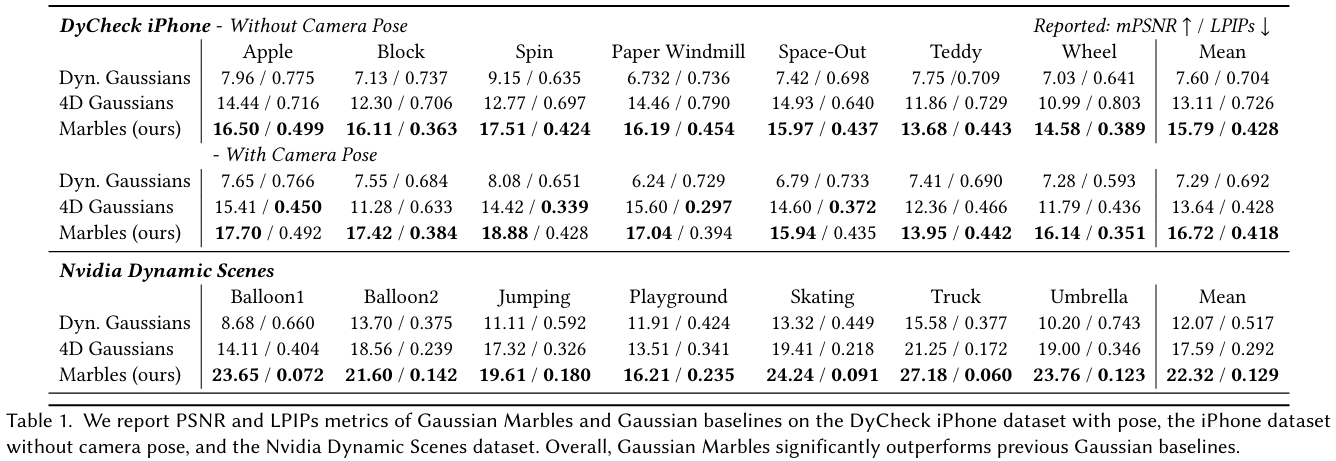
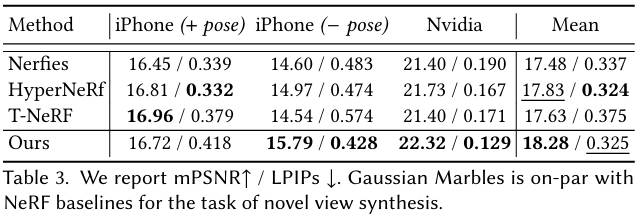
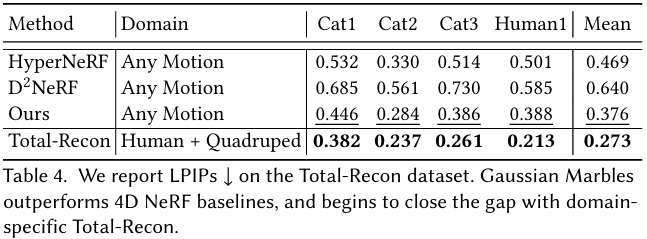
• Tracking and Editing :
  • TBD

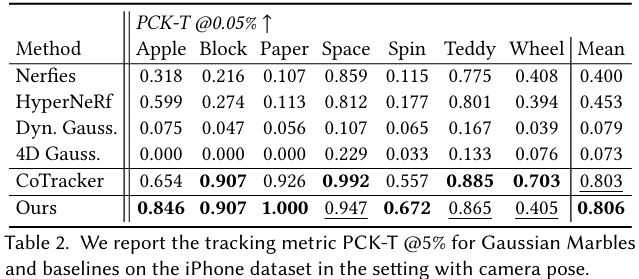
Ablation Study

• motion estimation :
  • frame 간의 motion 정보를 학습
  • locality and smoothness 보장
• global adjustment :
  • merge하고나서 global Gaussian이 specific frame을 잘 render하도록
  • global coherence 보장

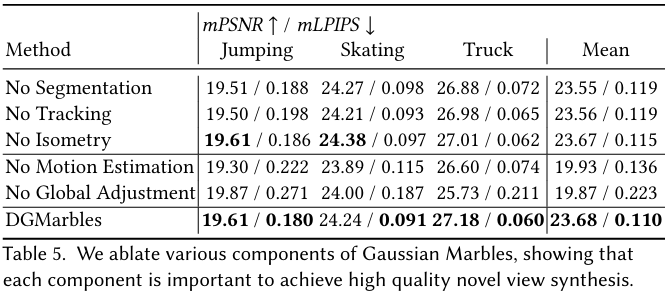
Conclusion

• Limitation :
  extremely challenging open-world dynamic and monocular novel-view-synthesis는 잘 못 함
  • 2D image prior에 의존하기 때문에
    SAM (segmentation), CoTracker (tracking), DepthAnything (depth estimation) 가 부정확할 경우
    결과 안 좋음
  • 3D geometric prior에도 의존하는데,
    rapid and non-rigid motion을 포함한 scene의 경우
    잘 대응 못 함

Question

• Q1 :
  Gaussian의 motion을 학습하는 것이라면 없던 object가 등장하거나 원래 있던 object가 frame 밖으로 벗어나는 경우에도 잘 대응할 수 있는지?
  CoTracker 등 여러 prior들도 위의 상황에 잘 대응하는지?

• A1 :
  TBD