SplineGS

Robust Motion-Adaptive Spline for Real-Time Dynamic 3D Gaussians from Monocular Video (CVPR 2025)

SplineGS - Robust Motion-Adaptive Spline for Real-Time Dynamic 3D Gaussians from Monocular Video (CVPR 2025)

Jongmin Park, Minh-Quan Viet Bui, Juan Luis Gonzalez Bello, Jaeho Moon, Jihyong Oh, Munchurl Kim

paper :
https://arxiv.org/abs/2412.09982
project website :
https://kaist-viclab.github.io/splinegs-site/

핵심 :

1. COLMAP-free :
   two-stage training strategy 사용
   즉, camera param.을 먼저 roughly estimate한 뒤 jointly optimize camera param. and 3DGS param.
2. dynamic scenes from in-the-wild monocular videos :
   static 3DGS와 dynamic 3DGS의 union
3. dynamic 3DGS’s mean :
   apply spline-based model (MAS) to each dynamic 3DGS mean (trajectories)
   이 때, depthmap과 camera param.를 이용해 2D track을 unproject하여 3D mean trajectories 초기화
4. thousands time faster than SOTA :
   more efficient than MLP-based or grid-based
5. loss :
   RGB image recon. loss
   depth recon. loss
   2D projection alignment loss
   3D alignment loss
   motion mask loss

Contribution

• novelty :
  • Motion-Adaptive Spline (MAS) :
    continuous dynamic 3DGS trajectories (deformation) 을 효율적으로 모델링하기 위해
    cubic Hermite splines with a small number of control points 사용
    • control point :
      • learnable param.
      • determines each piecewise cubic func.’s curvature and direction
    • initialization :
      2D track을 depthmap 이용하여 3D로 unproject
  • Motion-Adaptive Control points Pruning (MACP) :
    quality, efficiency 모두 챙기기 위해 계속 control points를 prune하여 수 조절
  • joint optimization strategy :
    photometric and geometric consistency loss 이용해서
    (external estimators 필요 X)
    camera param. 와 3DGS param.를 jointly optimize
    (COLMAP-free!)

Related Works

• dynamic novel-view-synthesis :
  • implicit representation (MLP) 이용하여 deformation 모델링 in canonical space [1], [2], [3], [4], [5]
    • 단점 : 아무리 tiny MLP더라도 computational overhead and low speed
  • 4D space-time domain을 multiple 2D planes로 decompose하는 grid-based model [6], 4DGS, [7], [8]
    • 단점 : grid representation으로는 scene의 dynamic 특징의 fine detail을 fully capture할 수 없음
  • polynomial trajectories 적용 [9]
    • 장점 : efficient (low cost)
    • 단점 : polynomial trajectory의 fixed degree는 complex motion을 표현하는 flexibility 측면에서 제한적임
• spline :
  • minimal number of control points로 complex shape를 smooth and continuous representation으로 표현할 수 있음
• SplineGS (본 논문) :
  • 논문 [10], [11]에서처럼
    각각 static bg와 moving object를 표현하기 위해
    3DGS를 static 3DGS와 dynamic 3DGS의 union으로 확장
    • static region :
      diffuse and specular features는 보존한 채
      time-encoded feature는 제거
    • dynamic region :
      mean \(\mu_{i}\) 는 deformation modeling에 의해 결정되는 time-dependent var.
      rotation \(q_{i}\) 와 scale \(s_{i}\) 도 time-dependent var.
  • 논문 STGS에서처럼
    final pixel color를 예측할 때 splatted feature rendering 사용 (SH coeff. 대신 feature!)

Method

Architecture

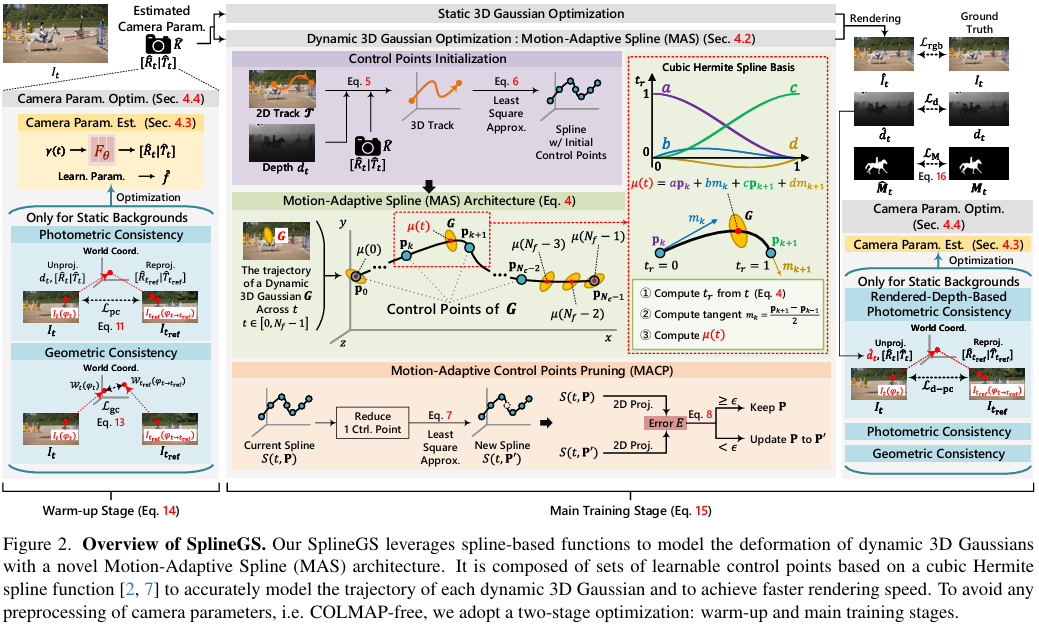
• goal :
  jointly optimize 3DGS param. and camera param.
  • camera param. :
    extrinsic \([\hat R_{t} | \hat T_{t}] \in R^{3 \times 4}\) for each time \(t\)
    and shared intrinsic \(\hat K \in R^{3 \times 3}\) across all \(t\)
  • how :
    two-stage optimization
    (warm-up stage and main traning stage)
    • warm-up stage :
      optimize coarse camera param.
      using photometric and geometric consistency
      (SfM 사용하지 않기 위해!)
    • main training stage :
      initialize 3DGS based on the estimated camera poses
      and
      jointly optimize 3DGS param. and camera param. with MAS and MACP

Motion-Adaptive Spline for 3DGS

time \(t\) 에서 each dynamic 3DGS의 mean \(\mu(t)\) (continuous trajectory)를 모델링하기 위해
cubic Hermite spline function with a set of learnable control points 사용 (MAS)
즉, each dynamic Gaussian마다 a set of control points가 있고 얘네들의 spline curve로 Gaussian mean \(\mu(t)\) 을 결정!

• Motion-Adaptive Spline (MAS) :
  \(\mu(t) = S(t, \boldsymbol P)\)
  • input :
    • time \(t\)
    • a set of \(N_{c}\) learnable control points
      \(\boldsymbol P = \{ \boldsymbol p_{k} | \boldsymbol p_{k} \in R^{3} \}\) where \(k \in [0, N_{c}-1]\)
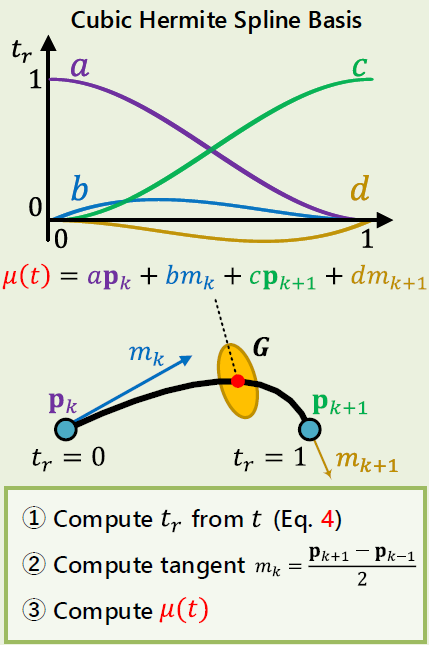
  • piece-wise cubic Hermite spline function \(S(\cdot)\) :
    \(S(t, \boldsymbol P) = (2t_{r}^{3} - 3t_{r}^{2} + 1) \boldsymbol p_{\lfloor t_{s} \rfloor} + (t_{r}^{3} - 2t_{r}^{2} + t_{r}) \boldsymbol m_{\lfloor t_{s} \rfloor} + (-2t_{r}^{3} + 3t_{r}^{2}) \boldsymbol p_{\lfloor t_{s} \rfloor + 1} + (t_{r}^{3} - t_{r}^{2}) \boldsymbol m_{\lfloor t_{s} \rfloor + 1}\)
    • \(N_{f}\) : frame (timestamp) 개수
    • \(N_{c}\) : control point 개수 (estimated by MACP)
    • \[t \in [0, N_{f} - 1]\]
    • \(t_{s} = t \frac{N_{c} - 1}{N_{f} - 1} \in [0, N_{c} - 1]\)
      e.g. 3.7
    • \(t_{r} = t_{s} - \lfloor t_{s} \rfloor\)
      e.g. 0.7
    • \(\boldsymbol m_{k} = (\boldsymbol p_{k+1} - \boldsymbol p_{k-1})/2\) : approx. tangent(기울기) of control point \(\boldsymbol p_{k}\)
    • piece-wise cubic Hermite spline function :
      \(\lfloor t_{s} \rfloor = 3\) 에서의 control point 및 tangent와
      \(\lfloor t_{s} \rfloor + 1 = 4\) 에서의 control point 및 tangent와
      그 사이 어디쯤 있는지 \(t_{r} = 0.7\) 를 이용하여
      \(\lfloor t_{s} \rfloor = 3\) 과 \(\lfloor t_{s} \rfloor + 1 = 4\) 사이의 piece-wise cubic Hermite spline function을 그림

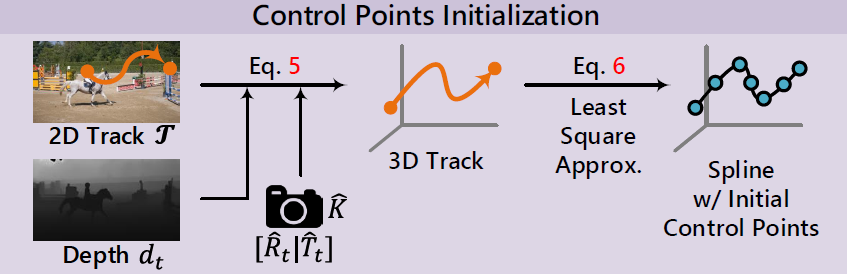
• Initialization of 3D Control Points :
  intialization은 quality에 매우 중요!
  long-range 2D track [12]과 depth [13] prior 사용
  • notation :
    • 2D track by [12] : \(\mathcal{T} = \left\{ \varphi_{t}^{tr} | \varphi_{t}^{tr} \in R^{2} \right\}_{t \in [0, N_{f} - 1]}\)
      where \(\varphi_{t}^{tr}\) : 2D track on pixel-coordinate at time \(t\)
    • projection func. from 3D camera-space to 2D image-space by intrinsic \(K\) : \(\pi_{K}(\cdot)\)
  • Step 1)
    unproject 2D track \(\mathcal{T}\) on image-space into 3D track curve on world-space
    using depth \(d_{t}\) and coarsely-estimated camera param. \(\hat K, [\hat R_{t} | \hat T_{t}]\)
    \(W_{t}(\varphi_{t}^{tr}) = \hat R_{t}^{T} \pi_{\hat K}^{-1}(\varphi_{t}^{tr}, d_{t}(\varphi_{t}^{tr})) - \hat R_{t}^{T} \hat T_{t}\)
    • we estimate camera param. \(\hat K, \hat R, \hat T\) from only frames (without any GT)
  • Step 2)
    initialize per-Gaussian control points set \(\boldsymbol P\)
    by least-square approx. s.t. spline curve \(S(t, \boldsymbol P)\) fits the initial tracker curve \(W_{t}(\varphi_{t}^{tr})\)
    \(\text{min}_{\boldsymbol P} \sum_{t=0}^{N_{f} - 1} \| W_{t}(\varphi_{t}^{tr}) - S(t, \boldsymbol P) \|^{2}\)

• Motion-Adaptive Control Points Pruning (MACP) :
  • issue :
    • control points 수가 너무 많으면
      spline curve가 over-fitting되고 speed가 느려짐
    • scene마다 motion의 종류와 정도가 각기 다르므로
      control points 수 for each dynamic 3DGS 는 scene에 맞춰서 need to be adaptively adjusted
  • solution :
    sparser control points로 prune하기 위해
    every 3DGS densification이 끝날 때마다 new spline function \(\mu(t) = S(t, \boldsymbol P')\) 계산
    where \(\boldsymbol P' = \left\{ \boldsymbol p_{l}' | \boldsymbol p_{l}' \in R^{3} \right\}_{l \in [0, N_{c} - 2]}\) : a set of \(N_{c} - 1\) control points
    (current set \(\boldsymbol P\) 보다 control point 1개 더 적음)
  • Step 1)
    1개 적은 control point set으로도 최대한 비슷한 spline curve를 만들도록 least-square approx.
    \(\text{min}_{\boldsymbol P'} \sum_{t=0}^{N_{f}-1} \| S(t, \boldsymbol P) - S(t, \boldsymbol P') \|^{2}\)
  • Step 2)
    \(S(t, \boldsymbol P)\) 와 \(S(t, \boldsymbol P')\) 간의 error \(E\) 가 작을 때만 a set of control points 업데이트
    \(\boldsymbol P = \begin{cases} \boldsymbol P' & \text{if} & E \lt \epsilon \\ \boldsymbol P & O.W. \end{cases}\)
    where error \(E = \frac{1}{N_{f}} \sum_{t=0}^{N_{f} - 1} \| \pi_{\hat K}(\hat R_{t} S(t, \boldsymbol P) + \hat T_{t}) - \pi_{\hat K} (\hat R_{t} S(t, \boldsymbol P') + \hat T_{t} \|^{2}\)
    (각 timestamp \(t\) 에서 3D mean on spline curve를 2D로 project시킨 뒤 차이 비교)
  • 의의 :
    each dynamic 3DGS마다 a set of control points를 따로 가지고 있는데,
    MACP 덕분에 각 dynamic 3DGS가 각기 다른 수의 control points를 가질 수 있고,
    motion이 복잡한 part는 control points 수가 많고
motion이 단순한 part는 control poitns 수가 적은 방식으로
    scene에 adaptively adjust 가능

Camera Pose Estimation

• Camera Pose :
  • extrinsic :
    \([\hat R_{t} | \hat T_{t}] = F_{\theta}(\gamma(t))\)
    • extrinsic 은 time에 대한 function
    • notation :
      • \(\gamma(\cdot)\) : positional encoding
      • \(F_{\theta}\) : shallow MLP
  • intrinsic (focal length) :
    • focal length \(\hat f\) 는 learnable param. shared across all frames in monocular video

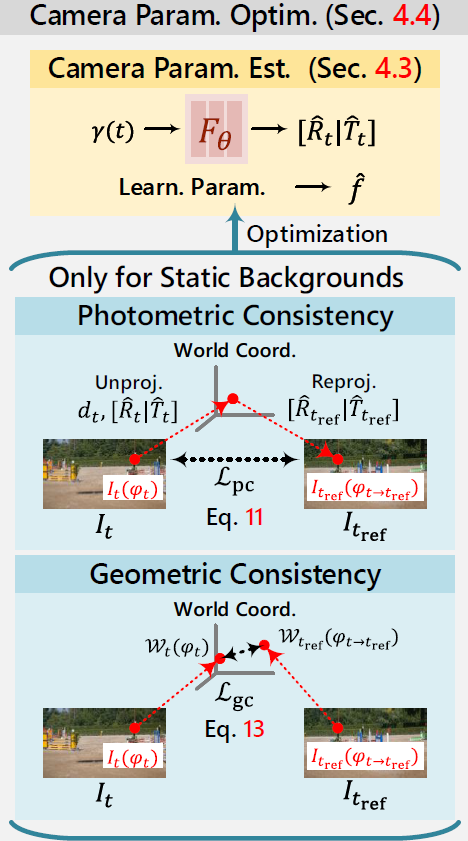
• Loss for optimizing Camera Pose :
  • Loss 1) photometric consistency : projection alignment
    • 목적 :
      target frame \(t\) 의 pixel \(i\) 가 reference frame \(t_{ref}\) 의 pixel \(j\) 로 projection 되었을 때
      reference frame’s pixel \(j\) 의 color \(I_{t_{ref}}(\varphi_{t \rightarrow t_{ref}})\) 가
      target frame’s pixel \(i\) 의 color \(I_{t}(\varphi_{t})\) 와 일치하도록
    • notation :
      • \(\varphi_{t}\) : target frame’s pixel-coordinate
      • \(\varphi_{t \rightarrow t_{ref}} = \pi_{\hat K} (\hat R_{t_{ref}} (\hat R_{t}^{T} \pi_{\hat K}^{-1} (\varphi_{t}, d_{t}(\varphi_{t})) - \hat R_{t}^{T} \hat T_{t}) + \hat T_{t_{ref}})\) : reference frame’s pixel-coordinate corresponding to \(\varphi_{t}\)
        (2D target frame \(t\)’s pixel-coordinate \(\rightarrow\) 3D location world-coordinate \(\rightarrow\) 2D reference frame \(t_{ref}\)’s pixel-coordinate)
    • loss :
      \(L_{pc} = \sum_{\varphi_{t}} \| M_{t, t_{ref}}(\varphi_{t}) \circledast (I_{t}(\varphi_{t}) - I_{t_{ref}}(\varphi_{t \rightarrow t_{ref}})) \|^{2}\)
      • \(M_{t, t_{ref}} = M_{t}(\varphi_{t}) M_{t_{ref}}(\varphi_{t \rightarrow t_{ref}})\) : union motion mask
        (dynamic objects는 color 변하는 게 당연하니까 제거하고, static region에 대해서만 loss 걸어줌)
        (\(M_{t}\) 와 \(M_{t_{ref}}\) 는 각각 \(I_{t}\) 와 \(I_{t_{ref}}\) 로부터 미리 계산한 motion mask [14])
  • Loss 2) geometric consistency : 3D alignment
    • 목적 :
      target frame \(t\) 의 pixel \(i\) 가 reference frame \(t_{ref}\) 의 pixel \(j\) 로 projection 되었을 때
      reference frame’s pixel \(j\) 를 3D location on world-coordinate으로 unproject시킨 \(W_{t_{ref}}(\varphi_{t \rightarrow t_{ref}})\) 가
      target frame’s pixel \(i\) 를 3D location on world-coordinate으로 unproject시킨 \(W_{t}(\varphi_{t})\) 와 일치하도록
    • notation :
      • \(W_{t}(\varphi_{t}) = \hat R_{t}^{T} \pi_{\hat K}^{-1}(\varphi_{t}, d_{t}(\varphi_{t})) - \hat R_{t}^{T} \hat T_{t}\) : unproject from pixel-coordinate to 3D world-coordinate
    • loss :
      \(L_{gc} = \sum_{\varphi_{t}} \| M_{t, t_{ref}}(\varphi_{t}) \circledast (W_{t}(\varphi_{t}) - W_{t_{ref}}(\varphi_{t \rightarrow t_{ref}})) \|^{2}\)

Loss

• Two-stage Optimization :
  • Stage 1) warm-up stage
    • optimize only camera param.
    • loss :
      \(L_{total}^{warm} = \lambda_{pc} L_{pc} + \lambda_{gc} L_{gc}\)
      • \(L_{pc}\) : photometric consistency (projection alignment)
      • \(L_{gc}\) : geometric consistency (3D alignment)
  • Stage 2) main training stage
    • Step 2-1)
      Stage 1)에서 coarsely 예측한 camera param. \(\hat K, \hat R, \hat T\) 를 이용하여
      각 dynamic 3DGS의 a set of control points 초기화
      (how? : 위의 Motion-Adaptive Spline for 3DGS 섹션에서 설명함)
    • Step 2-2)
      jointly optimize 3DGS param. and camera param.
    • loss :
      \(L_{total}^{main} = \lambda_{rgb} L_{rgb} + \lambda_{d} L_{d} + \lambda_{M} L_{M} + \lambda_{pc} L_{pc} + \lambda_{d-pc} L_{d-pc} + \lambda_{gc} L_{gc}\)
      • recon. loss :
        • \(L_{rgb}\) : L1 recon. loss b.w. rendered frame and GT frame
        • \(L_{d}\) : L1 recon. loss b.w. rendered depth and GT depth
      • alignment loss :
        • \(L_{pc}\) : photometric consistency (projection alignment)
        • \(L_{gc}\) : geometric consistency (3D alignment)
        • \(L_{d-pc}\) : additional photometric consistency (projection alignment)
          • prior depth [13] 대신 3DGS를 이용한 rendered depth 사용하여
            photometric consistency 계산
          • prior depth 대신 rendered depth를 사용하면
            estimated 3DGS geometry 의 도움을 받아
            joint optimization of camera param. and 3DGS param. 가능!
      • motion mask loss :
        • \(L_{M} = 1 - \text{f1-score} = 1 - \frac{2(\sum_{\varphi_{t}} M_{t}(\varphi_{t}) \hat M_{t}(\varphi_{t})) + \epsilon}{(\sum_{\varphi_{t}} M_{t}(\varphi_{t}) + \hat M_{t}(\varphi_{t})) + \epsilon}\) : binary dice loss
          b.w. pre-computed GT motion mask \(M_{t}\) from prior [14]
          and rendered motion mask \(\hat M_{t}\) from dynamic 3D Gaussians
          • rendered motion mask :
            \(\hat M_{t}(\varphi_{t}) = \sum_{i \in N} m_{i} \alpha_{i} \prod_{j=1}^{i-1} (1 - \alpha_{j})\)
            where \(m_{i} = 0\) if \(i\)-th 3DGS is static 3DGS, and \(m_{i} = 1\) if \(i\)-th 3DGS is dynamic 3DGS
            (즉, \(i\)-th 3DGS가 static인지, dynamic인지에 따른 \(m_{i}\) 를 accumulate 하여 motion mask로 rendering!)
        • binary dice loss는 highly imbalanced segmentation을 위해 제안되었듯이
          dynamic 3DGS와 static 3DGS를 더 잘 분리할 수 있게 해줌

Experiment

• Dataset :
  • NVIDIA dataset
    • evaluation configuration : [RoDynRF] 를 따름
    • dataset sampling : [NSFF] 를 따름
      • sample 24 timestamps
      • larger motion을 simulate하기 위해
        홀수 frames 제외
      • generalization을 위해
        test 시에 사용할 timestamps를 training할 때 제외
  • DAVIS dataset (avg. 70 frames per video)

Result

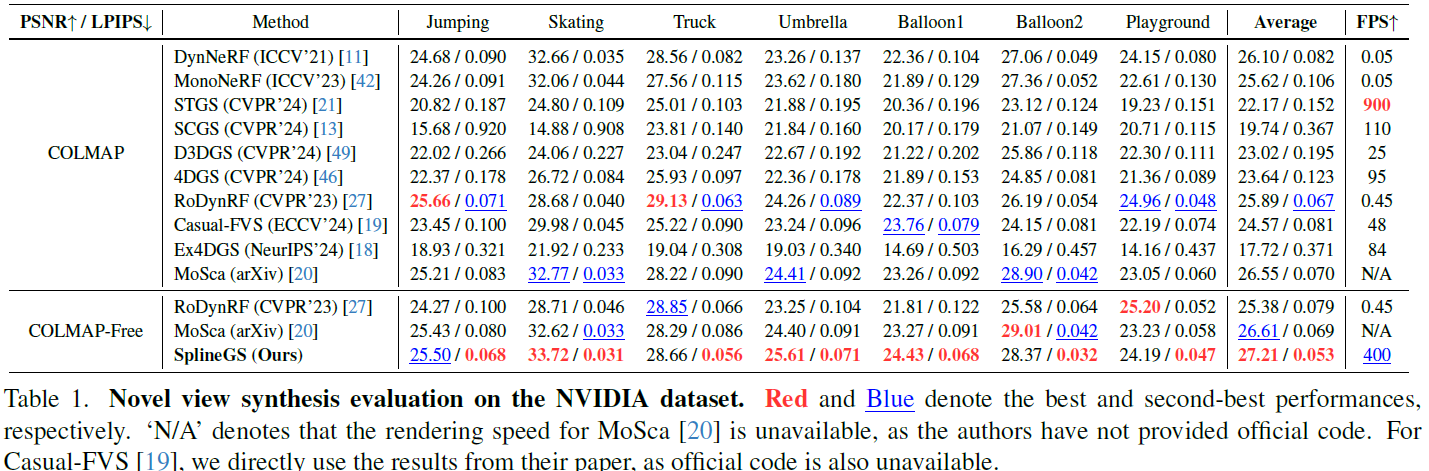
• Novel-View-Synthesis :
  • SOTA baseline :
    • COLMAP-based : [DynNeRF], [MonoNeRF], [STGS], [SCGS], [D3DGS], [4DGS], [RoDynRF], [CasualFVS], [Ex4DGS], [Mosca]
      • RoDynRF, DynNeRF : 느림
      • Ex4DGS, STGS : multi-view setting으로 설계되어 monocular video로 학습하면 시간에 따라 점점 inconsistent geometry alignment
      • D3DGS, STGS : SfM(COLMAP)이 DAVIS dataset에서 camera param. 및 initial pcd 잘 추정 못함
    • COLMAP-free : [RoDynRF], [Mosca]

• Novel View and Time Synthesis :
  • SOTA baseline :
    • NeRF-based : [DynNeRF], [RoDynRF]
      • RoDynRF, DynNeRF : unseen timestamp에 대해 artifacts 및 blurriness 생김
    • 3DGS-based : [STGS], [D3DGS], [4DGS]
      • STGS, D3DGS, 4DGS : unseen timestamp에 대해 더 심각한 degradation 생김
  • 본 논문 (SplineGS) :
    MAS(Motion-Adaptive Spline) 덕분에
    dynamic 3D Gaussian들을 효과적으로 deform시켜서
    시간에 따라 움직이는 물체의 continuous trajectories를 정확히 캡처할 수 있음
    • unseen timestamp에 대해서도 continuous trajectory로 잘 캡처 가능
    • temporal consistency는 아래의 tOF score로 확인 가능
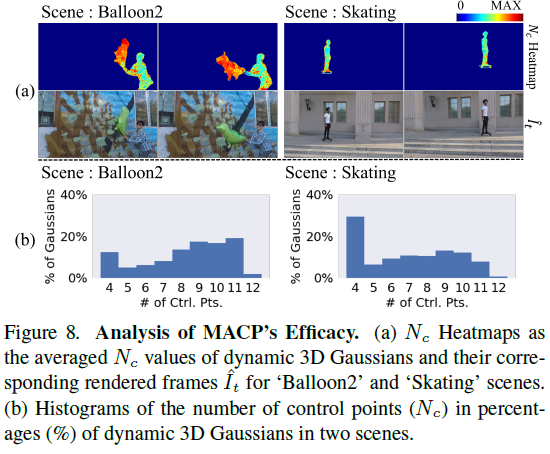
    • continuous trajectories 모델링 능력을 확인하기 위해
      아래 그림에 dynamic objects의 projected 2D motion tracking 결과도 있음

Ablation Study

• Motion-Adaptive Spline (MAS) :
  • baseline : various deformation models
    • MLP
      e.g. D3DGS
    • grid-based model
      e.g. 4DGS
    • polynomial func. of degree 3 or 10
      e.g. STGS
      (degree 10을 쓰면 numerical instability 때문에 noisier optimization으로 quality도 더 안 좋고, latency도 증가함)
    • Bezier curve
      (성능 비슷하게 좋지만, recursive 계산 때문에 MAS보다 latency 큼)

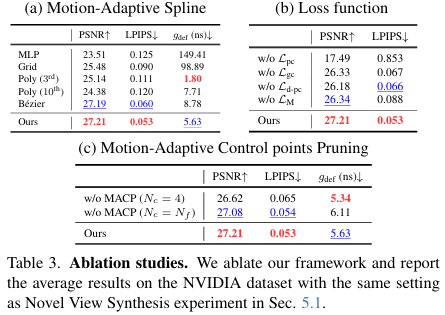
• Motion-Adaptive Control Points Pruning (MACP) :
  • baseline : fixed number of control points \(N_{c} = 4\) or \(N_{c} = N_{f}\)
  • MAS with MACP :
    good trade-off (latency 조금 증가하지만 rendering quality 많이 증가)

Skating scene처럼 simple motion인 경우에는 MACP 덕분에 최소한의 N_c로도 대부분의 dynamic 3DGS 표현 가능

Conclusion

• Limitation :
  • Prior 필요
    • depthmap (for all)
    • 2D track (for all)
    • motion mask (for \(L_{M}\))
  • in-the-wild video에서 camera 또는 object가 매우 빠르게 움직이는 경우 input frames 자체가 blurry한데,
    이러한 input frames의 흐림 자체가 rendering quality를 낮춤
    • 현재 가능한 solution :
      SOTA 2D deblurring methods를 pre-processing으로 먼저 input frames에 적용한 뒤 training에 사용
    • future work :
      따로 pre-processing하지 않고,
      deblurring method와 recon. pipeline을 통합하여
      joint deblurring and rendering optimization framework 구축
  • per-Scene model이라 feed-forward model로 확장 가능 ???

Question

• Q1 :
  photometric consistency loss에서 motion mask 값이 static region에 대해서만 0이라는데,
  dynamic object를 exclude한다는 문구로 미루어보아 (static region에만 loss를 걸어주기 위해)
  static region에 대해서 1이어야 하는 거 아닌가요?

• A1 :
  code implementation 한 번 보자

• Q2 :
  colmap을 안 쓰면 Gaussian mean initialization은 어떻게 하나요?

• A2 :
  per-Gaussian parameter로 Gaussian마다 a set of control points \(\boldsymbol P = \{ \boldsymbol p_{k} | \boldsymbol p_{k} \in R^{3} \}\) where \(k \in [0, N_{c}-1]\) 를 가지고 있고,
  depth prior와 coarsely-estimated camera param.로 2D track prior를 unproject한 뒤 LS approx.로 a set of control points \(\boldsymbol P\) 를 initialize (그러면 arbitrary timestep \(t\) 에서의 Gaussian mean은 해당 spline function 위에 있게 됨)

• Q3 :
  MACP로 control point를 하나 뺄 대 어떤 control point를 빼나요?

• A3 :
  하나 적은 control points’ set으로 new spline function \(S(t, \boldsymbol P)\) 를 다시 만들고, control point들은 time에 대해 균등하게 배치

• Q4 :
  colmap-free라서 camera parameter를 추정한다고 할 때 요즘 논문들은 보편적으로 depth prior를 활용하여 학습을 통해 추정하나요?

• A4 :
  아니요, NoPoSplat 같은 논문을 보면 depth prior 없어도 transformer가 photometric loss만으로 camera parameter 추정하기도 합니다

• Q5 :
  two-stage로 나눠서 학습을 통해 먼저 camera parameter를 추정하려면 training time이 더 오래 걸릴텐데, COLMAP pre-processing 쓰지 않고 직접 camera parameter를 추정하는 이유가 뭔가요?

• A5 :
  COLMAP으로 camera pose를 pre-compute 해놓는 건 in-the-wild video에서 별로 성능 안 좋음 (특히 원형 호수 같은 images에서는 COLMAP 성능 꽝). 그래서 차라리 직접 학습을 통해 camera parameter를 추정하는 게 더 성능 좋음

• Q6 :
  dynamic NVS modeling 기법 중에 Spline-based representation이 갖는 장점은?

• A6 :
  • grid-based modeling - 단점 : struggle to fully capture the fine details
    e.g. HexPlane, 4DGS
  • polynomial modeling - 단점 : fixed degree restricts flexibility for complex motions
  • spline-based modeling - 장점 : explicit spline function이 continuous trajectory를 보장해서 unseen novel timestamp에 대해서도 생각보다 퀄리티 괜찮음

• Q7 :
  camera parameter를 추정할 때 unproject함으로써 photometric consistency와 geometric consistency를 이용하는데,
  만약에 카메라(extrinsic)가 고정된 채 scene content만 dynamic하게 움직이는 경우에는 해당 두 가지 loss가 잘 작동하지 않을 것 같습니다

• A7 :
  맞는 말입니다. 하지만 dataset 중에 dynamic scene을 찍는 카메라가 움직이지 않는 경우는 거의 없고, camera movement가 작은 DAVIS data가 있긴 한데 거기서도 해당 모델이 잘 작동하긴 했습니다.