FMANet

• FMA-Net : Flow-Guided Dynamic Filtering and Iterative Feature Refinement with Multi-Attention for Joint Video Super-Resolution and Deblurring
  • Geunhyuk Youk, Jihyong Oh, Munchurl Kim
• Abstract
• Related Work
• Method
• Results
• Conclusion
• Limitation

FMA-Net : Flow-Guided Dynamic Filtering and Iterative Feature Refinement with Multi-Attention for Joint Video Super-Resolution and Deblurring

Geunhyuk Youk, Jihyong Oh, Munchurl Kim

paper :
https://arxiv.org/abs/2401.03707
project website :
https://kaist-viclab.github.io/fmanet-site/
pytorch code :
https://github.com/KAIST-VICLab/FMA-Net

---

Abstract

Task : Joint learning of VSRDB (video super-resolution and deblurring)

• restore HR video from blurry LR video
  challenging because should handle two types of degradation (SR and deblurring) simultaneously
• super-resolution : LR vs HR
• deblurring : blurry vs sharp

FGDF (flow-guided dynamic filtering)

• precise estimation of both spatio-temporally-variant degradation and restoration kernels that are aware of motion trajectories (not stick to fixed positions)
• effectively handle large motions with small-sized kernels (naive dynamic filtering의 한계 극복)

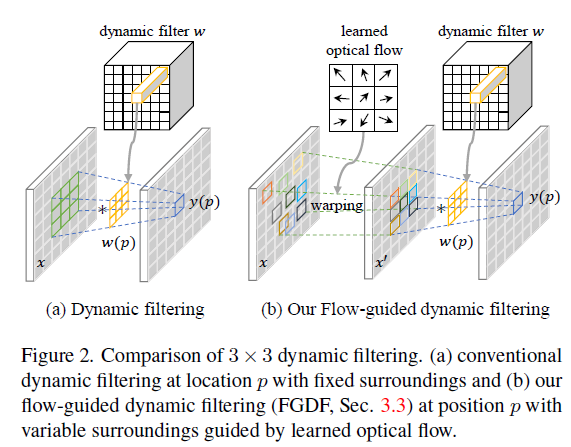
DCN (Deformable Conv.) : learn position-invariant \(n \times n\) filter coeff.
vs
DF (Dynamic filtering) : learn position-wise \(n \times n\) dynamic filter coeff.

DF (Dynamic Filtering) : fixed surroundings
vs
FGDF (Flow Guided DF) : variable surroundings by learned optical flow

FRMA (iterative feature refinement with multi-attention)

refine features by iterative updates
loss : TA (temporal anchor)
multi-attention :

• center-oriented attention (focus on target frame)
• degradation-aware attention (use degradation kernels in globally adaptive manner)

---

Related Work

VSR (Video Super-Resolution)

Based on the number of input frames,

1. sliding window-based method : recover HR frames by using neighboring frames within a sliding window
   use CNN, optical flow estimation, deformable conv., or transformer focusing on temporal alignment
   vs
2. recurrent-based method : sequentially propagate the latent features of one frame to the next frame
   Chan et al. [1] BasicVSR++ : combine bidirectional propagation of past and future frames into current frame features
   limit : gradient vanishing

DB (Video Deblurring)

Zhang et al. [2] 3D CNN
Li et al. [3] grouped spatial-temporal shifts
transformer-based : Restormer [4], Stripformer [5], RVRT [6]

Joint learning of VSRDB (not sequential cascade of VSR and DB)

Previous works are mostly designed for ISRDB

Fang et al. [7] HOFFR : the first deep-learning-based VSRDB
limit : struggle to deblur spatially-variant motion blur because 2D CNN has spatially-equivariant and input-independent filters

Dynamic Filter Network

predict spatially-variant degradation or restoration kernels

Zhou et al. [8] :
spatially adaptive deblurring filter for recurrent video deblurring
Kim et al. [9] KOALAnet :
blind SR predicts spatially-variant degradation and upsampling filters

• limit : apply dynamic filtering only to the reference frame (target position and its fixed surrounding neighbors), so cannot accurately exploit spatio-temporally-variant-motion info. from adjacent frames
• limit : if apply dynamic filtering to adjacent frames \(\rightarrow\) large-sized filters are required to capture large motions \(\rightarrow\) high computational complexity
• limit : [10] suggested two separable large 1D kernels to approximate a large 2D kernel \(\rightarrow\) does not capture fine detail, so inappropriate for video

---

Method

Overview

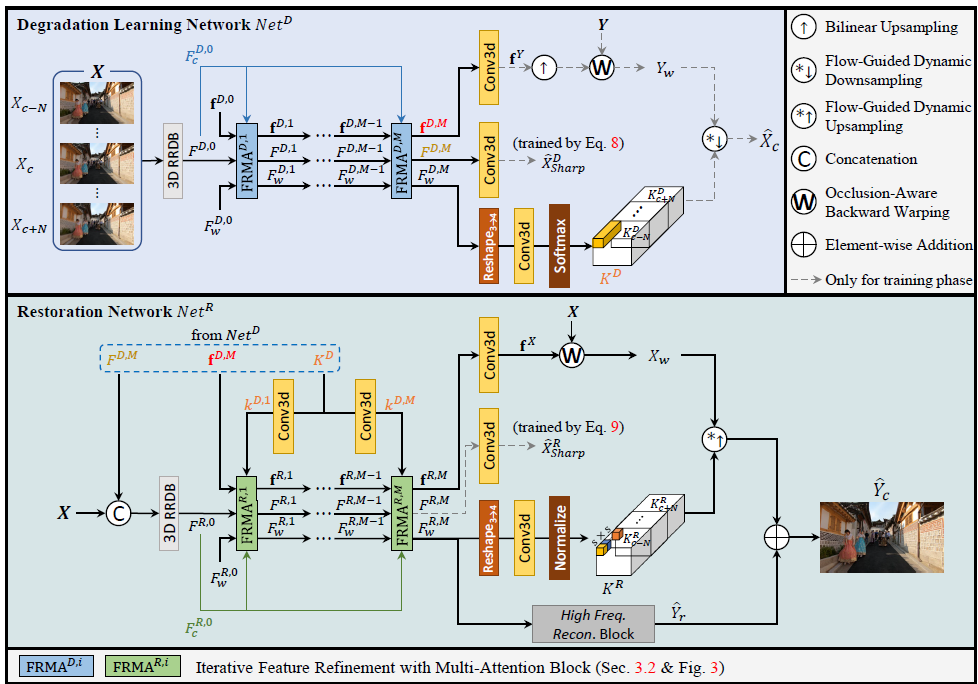
FMA-Net : VSRDB framework based on FGDF and FRMA
allow for small-to-large motion representation learning

• input : blurry LR sequence \(X = \left\lbrace X_{c-N}:X_{c+N} \right\rbrace \in R^{T \times H \times W \times 3}\) where \(T=2N+1\) and \(c\) is a center frame index
• goal : predict sharp HR center frame \(\hat Y_{c} \in R^{sH \times sW \times 3}\) where \(s\) is SR scale factor

1. degradation learning network \(Net^{D}\) : learn motion-aware spatio-temporally-variant degradation kernels
2. restoration network \(Net^{R}\) : utilize these degradation kernels in a globally adaptive manner to restore center frame \(X_c\)
3. \(Net^{D}\) and \(Net^{R}\) consist of FRMA blocks and FGDF module

FRMA block

pre-trained optical flow network : unstable for blurry frames and computationally expensive

vs

FRMA block :
learn self-induced optical flow in a residual learning manner
learn multiple optical flows with corresponding occlusion masks
\(\rightarrow\) flow diversity enables to learn one-to-many relations b.w. pixels in a target frame and its neighbor frames
\(\rightarrow\) beneficial since blurry frame's pixel info. is spread due to light accumulation

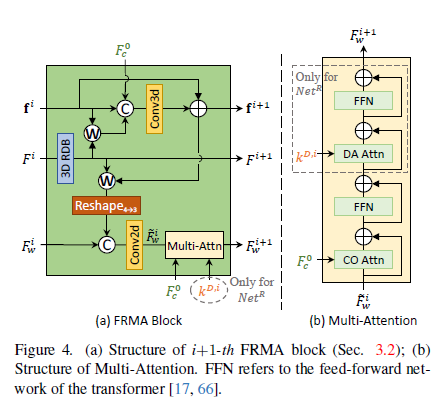
Three features

1. \(F \in R^{T \times H \times W \times C}\) :
   temporally-anchored (unwarped) feature at each frame index \(0 \sim T-1\)
   dim. T에 걸친 전체 feature
2. \(F_w \in R^{H \times W \times C}\) :
   warped feature
   target frame feature 관련
3. \(\boldsymbol f = \left \lbrace f_{c \rightarrow c+t}^{j}, o_{c \rightarrow c+t}^{j} \right \rbrace _{j=1:n}^{t=-N:N} \in R^{T \times H \times W \times (2+1)n}\) :
   multi-flow-mask pairs
   \(f_{c \rightarrow c+t}^{j}\) : learnable optical flow
   \(o_{c \rightarrow c+t}^{j}\) : learnable occlusion mask (sigmoid for stability)
   \(n\) is the number of multi-flow-mask pairs from the center frame index \(c\) to each frame index
   왜 dim. (2+1)??? \(\rightarrow\) optical flow \(R^2\) and occlusion mask \(R^1\)

(i+1)-th Feature Refinement : 위첨자로 표기
feature refine 식 기원?? \(\rightarrow\) BasicVSR++에서 아이디어 따와서 iterative하게 변형

1. \(F^{i+1}\)=RDB(\(F^{i}\)) :
   RDB [11]
2. \(\boldsymbol f^{i+1}\) = \(\boldsymbol f^{i}\) + Conv3d(concat(\(\boldsymbol f^{i}\), \(W\)(\(F^{i+1}\), \(\boldsymbol f^{i}\)), \(F_{c}^{0}\)))
   \(W\)(\(F^{i+1}\), \(\boldsymbol f^{i}\)) : warp \(F^{i+1}\) to center frame index \(c\) based on \(f^{i}\)
   \(W\) : occlusion-aware backward warping
   concat : along channel dim.
   \(F_{c}^{0} \in R^{H \times W \times C}\) : feature map at center frame index \(c\) of the initial feature \(F^{0} \in R^{T \times H \times W \times C}\)
3. \(\tilde F_{w}^{i}\) = Conv2d(concat(\(F_{w}^{i}\), \(r_{4 \rightarrow 3}\)(\(W\)(\(F^{i+1}\), \(\boldsymbol f^{i+1}\)))))
   \(r_{4 \rightarrow 3}\) : reshape from \(R^{T \times H \times W \times C}\) to \(R^{H \times W \times TC}\) for feature aggregation
4. \(F_w^{i+1}\) = Multi-Attn(\(\tilde F_{w}^{i}\), \(F_{c}^{0}\)(, \(k^{D, i}\)))

RDB Network [11] :
TBD

RRDB Network [15] :
TBD

Occlusion-Aware Backward Warping [12] [13] [14] :
TBD

Multi-Attention :

• CO(center-oriented) attention :
  better align \(\tilde F_{w}^{i}\) to \(F_{c}^{0}\) (center feature map of initial temporally-anchored feature)
• DA(degradation-aware) attention :
  \(\tilde F_{w}^{i}\) becomes globally adaptive to spatio-temporally variant degradation by using degradation kernels \(K^{D}\)

• CO attention :
  \(Q=W_{q} F_{c}^{0}\)
  \(K=W_{k} \tilde F_{w}^{i}\)
  \(V=W_{v} \tilde F_{w}^{i}\)
  \(COAttn(Q, K, V) = softmax(\frac{QK^{T}}{\sqrt{d}})V\)
  실험 결과, \(\tilde F_{w}^{i}\)가 자기 자신(self-attention)이 아니라 \(F_{c}^{0}\)과의 relation에 집중할 때 better performance

• DA attention :
  CO attention과 비슷하지만,
  Query 만들 때 \(F_{c}^{0}\) 대신 \(k^{D, i}\) 사용
  \(\tilde F_{w}^{i}\) becomes globally adaptive to spatio-temporally-variant degradation
  \(k^{D, i} \in R^{H \times W \times C}\) : degradation features adjusted by conv. with \(K^{D}\) (motion-aware spatio-temporally-variant degradation kernels) 에 대해
  \(Q=W_{q} k^{D, i}\)
  DA attention은 \(Net^{D}\) 말고 \(Net^{R}\) 에서만 사용

FGDF

• spatio-temporal Dynamic Filter :
  \(y(p) = \sum_{t=-N}^{N} \sum_{k=1}^{n^2} F_{c+t}^{p}(p_k) x_{c+t}(p+p_k)\)
  where
  \(c\) : center frame index
  \(p_k \in \{ (- \lfloor \frac{n}{2} \rfloor, - \lfloor \frac{n}{2} \rfloor), \cdots , (\lfloor \frac{n}{2} \rfloor, \lfloor \frac{n}{2} \rfloor) \}\) : sampling offset for conv. with \(n \times n\) kernel
  \(F \in R^{T \times H \times W \times n^{2}}\) : predicted \(n \times n\) dynamic filter
  \(F^p \in R^{T \times n^{2}}\) : predicted \(n \times n\) dynamic filter at position p

• limit :
  fixed position (\(p\)) and fixed surrounding neighbors (\(p_k\))
  \(\rightarrow\) To capture large motion, require large-sized filter

solution : FGDF
kernels - dynamically generated / pixel-wise (position-wise) / variable surroundings guided by optical flow
\(\rightarrow\) can handle large motion with relatively small-sized filter
\(y(p) = \sum_{t=-N}^{N} \sum_{k=1}^{n^2} F_{c+t}^{p}(p_k) x_{c+t}^{\ast}(p+p_k)\)
where
\(x_{c+t}^{\ast} = W(x_{c+t}, \boldsymbol f_{c+t})\) : warped input feature based on \(\boldsymbol f_{c+t}\)
\(\boldsymbol f_{c+t}\) : flow-mask pair from frame index \(c\) to \(c+t\)

Overall Architecture

Degradation Network \(Net^{D}\)
input : blurry LR sequence \(\boldsymbol X\) and sharp HR sequence \(\boldsymbol Y\)
goal : predict flow and degradation kernels in sharp HR sequence \(\boldsymbol Y\)

1. an image flow-mask pair \(\boldsymbol f^{Y}\)
2. motion-aware spatio-temporally-variant degradation kernels \(K^{D}\)
   \(\rightarrow\) obtain blurry LR center frame \(\boldsymbol X_{c}\) from sharp HR counterpart \(\boldsymbol Y\)

• step 1-1. initialize
  RRDB : [15]
  \(\boldsymbol X \rightarrow\) 3D RRDB \(\rightarrow F^{0}\)

• step 1-2. initialize
  \(F_{w}^{0} = 0\), \(\boldsymbol f = \left \lbrace f_{c \rightarrow c+t}^{j} = 0, o_{c \rightarrow c+t}^{j} = 1 \right \rbrace _{j=1:n}^{t=-N:N}\)

• step 2. M FRMA blocks
  \(F^{0}, F_{w}^{0}, \boldsymbol f^{0} \rightarrow\) \(M\) FRMA blocks \(\rightarrow F^{M}, F_{w}^{M}, \boldsymbol f^{M}\)

• step 3-1. an image flow-mask pair \(\boldsymbol f^{Y} \in R^{T \times H \times W \times (2+1) 1}\)
  \(\boldsymbol f^{M} \rightarrow\) Conv3d \(\rightarrow \boldsymbol f^{Y}\)

• step 3-2. \(\hat X_{sharp}^{D}\) only used in Temporal Anchor (TA) loss
  \(F^{M} \rightarrow\) Conv3d \(\rightarrow \hat X_{sharp}^{D} \in R^{T \times H \times W \times 3}\) in image domain

• step 3-3. motion-aware spatio-temporally-variant degradation kernels \(K^{D} \in R^{T \times H \times W \times k_{d}^{2}}\)
  \(K^{D}\) = softmax(Conv3d(\(r_{3 \rightarrow 4}\)(\(F_{w}^{M}\))))
  where
  \(k_{d}\) : degradation kernel size
  sigmoid for normalization : all kernels have positive values, which mimics blur generation process

• step 4. FGDF downsampling to predict blurry center frame \(\hat X_{c}\)
  \(\hat X_{c}\) = \(W(\boldsymbol Y, s (\boldsymbol f^{Y} \uparrow _{s}))\) \(\circledast K^{D} \downarrow _{s}\)
  where
  \(\uparrow\) : \(\times s\) bilinear upsampling
  \(W(\boldsymbol Y, s (\boldsymbol f^{Y} \uparrow _{s}))\) : warped sharp HR sequence based on an upsampled image flow-mask pair
  \(\circledast K^{D} \downarrow _{s}\) : FGDF with filter \(K^{D}\) with stride \(s\)

Restoration Network \(Net^{R}\)
input : blurry LR sequence \(\boldsymbol X\) and \(F^{M}, \boldsymbol f^{M}, K^{D}\) from \(Net^{D}\)
goal : predict flow and restoration kernels in blurry LR sequence \(\boldsymbol X\)

1. an image flow-mask pair \(\boldsymbol f^{X}\)
2. restoration kernels \(K^{R}\)
   \(\rightarrow\) obtain sharp HR center frame \(\hat Y_{c}\) from blurry LR counterpart \(\boldsymbol X\)

• step 1-1. initialize \(F^{0}\)
  RRDB : [15]
  concat(\(\boldsymbol X\), \(F^{M}\) from \(Net^{D}\)) \(\rightarrow\) 3D RRDB \(\rightarrow\) \(F^{0}\)

• step 1-2. initialize \(F_{w}^{0}\), \(\boldsymbol f^{0}\)
  \(F_{w}^{0} = 0\), \(\boldsymbol f^{0} = \boldsymbol f^{M}\) from \(Net^{D}\)

• step 2-1. compute \(k^{D, i} \in R^{H \times W \times C}\) for DA attention

• step 2-2. M FRMA blocks
  \(F^{0}, F_{w}^{0}, \boldsymbol f^{0}, k^{D, i} \rightarrow\) \(M\) FRMA blocks \(\rightarrow F^{M}, F_{w}^{M}, \boldsymbol f^{M}\)

• step 3-1. an image flow-mask pair \(\boldsymbol f^{X} \in R^{T \times H \times W \times (2+1) 1}\)
  \(\boldsymbol f^{M} \rightarrow\) Conv3d \(\rightarrow \boldsymbol f^{X}\)

• step 3-2. \(\hat X_{sharp}^{R}\) only used in Temporal Anchor (TA) loss
  \(F^{M} \rightarrow\) Conv3d \(\rightarrow \hat X_{sharp}^{R} \in R^{T \times H \times W \times 3}\) in image domain

• step 3-3. motion-aware spatio-temporally-variant \(\times s\) upsampling and restoration kernels \(K^{R} \in R^{T \times H \times W \times s^{2} k_{r}^{2}}\)
  \(K^{R}\) = Normalize(Conv3d(\(r_{3 \rightarrow 4}\)(\(F_{w}^{M}\))))
  where
  \(k_{r}\) : restoration kernel size
  Normalize : w.r.t all kernels at temporally co-located positions over \(X\) (\(T\) dim.에 대해 normalize)

• step 3-4. high-frequency detail \(\hat Y_{r}\)
  \(F_{w}^{M} \rightarrow\) stacked conv. and pixel shuffle \(\rightarrow \hat Y_{r}\)

• step 4. FGDF upsampling to predict sharp center frame \(\hat Y_{c}\)
  \(\hat Y_{c}\) = \(\hat Y_{r}\) + \(W(\boldsymbol X, \boldsymbol f^{X})\) \(\circledast K^{D} \uparrow _{s}\)
  where
  \(W(\boldsymbol X, \boldsymbol f^{X})\) : warped blurry LR sequence based on an image flow-mask pair
  \(\circledast K^{D} \uparrow _{s}\) : \(\times s\) dynamic upsampling with kernel \(K^{R}\)

Training

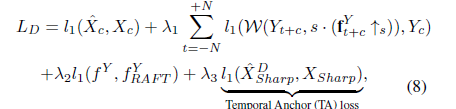
Stage 1. Pre-train \(Net^{D}\)

• loss 1. reconstruction loss for blurry LR \(X_{c}\)
  \(\hat X_{c}\) \(\leftrightarrow\) \(X_{c}\)
• loss 2. optical flow warping loss (warping from c to c+t) in \(\boldsymbol Y\)
  \(W(Y_{t+c}, s (\boldsymbol f_{t+c}^{Y} \uparrow _{s}))\) \(\leftrightarrow\) \(Y_{c}\)
• loss 3. optical flow refining loss in \(\boldsymbol Y\)
  \(f^{Y}\) \(\leftrightarrow\) \(f_{RAFT}^{Y}\)
  where
  \(f^{Y}\) is image optical flow (no occlusion mask) contained in \(\boldsymbol f^{Y}\)
  \(f_{RAFT}^{Y}\) is pseudo-GT optical flow by pre-trained RAFT model [16]
• loss 4. Temporal Anchor (TA) loss for sharp LR \(X_{sharp}\)
  It anchors and sharpens each feature w.r.t corresponding frame index
  \(\hat X_{sharp}^{D}\) \(\leftrightarrow\) \(X_{sharp}\)
  where
  sharp HR sequence \(\boldsymbol Y \rightarrow\) bicubic downsampling \(\rightarrow\) GT sharp LR sequence \(X_{sharp}\)
  \(\rightarrow\) keep each feature temporally anchored for the corresponding frame index
  \(\rightarrow\) constrain the solution space to distinguish warped and unwarped features
  ???
  \(\rightarrow\) iteratively 학습하다보니 frame 0, 1, 2의 features인 \(F \in R^{T \times H \times W \times C}\) 가 점점 target frame 1의 feature인 \(F_w\) 에 가깝게 frame 0.7,, 1, 1.3 느낌으로 업데이트됨
  \(\rightarrow\) \(F \in R^{T \times H \times W \times C}\) 의 특성을 유지하도록 downsampled \(\boldsymbol Y\)와 비교하는 Temporal Anchor (TA) loss 추가!

RAFT: Recurrent all-pairs field transforms for optical flow [16] :
핵심 아이디어 : TBD

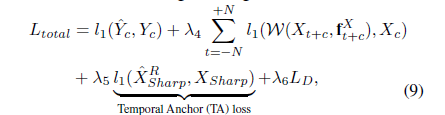
Stage 2. Jointly train \(Net^{D}\) and \(Net^{R}\)

• loss 1. restoration loss for sharp HR \(Y_{c}\)
  \(\hat Y_{c}\) \(\leftrightarrow\) \(Y_{c}\)
• loss 2. optical flow warping loss (warping from c to c+t) in \(\boldsymbol X\)
  Stage 1.의 loss 2.와 동일한 원리
• loss 3. Temporal Anchor (TA) loss for sharp LR \(X_{sharp}\)
  Stage 1.의 loss 4.와 동일한 원리
• loss 4. \(L_{D}\)
  Stage 1.의 loss들
  왜 X optical flow에 대해선 RAFT loss 안 했지??
  \(\rightarrow\) RAFT model에서 구한 optical flow는 sharp HR sequence에 대한 거라서!

---

Results

Settings

LR patch size : 64 \(\times\) 64
the number of FRMA blocks : \(M\) = 4
the number of multi-flow-mask pairs : \(n\) = 9
degradation and restoration kernel size : \(k_{d}\), \(k_{r}\) = 20, 5
the number of frames in sequence : \(T\) = 3 (\(N\) = 1)
ratio b.w. HR and LR : \(s\) = 4
multi-attention block : utilize multi-Dconv head transposed attention (MDTA) and Gated-Dconv feed-forward network (GDFN) from Restormer [4]

multi-Dconv head transposed attention and Gated-Dconv feed-forward network [4] :
TBD

Datasets and Evaluation Metrics

• Datasets :
  REDS dataset : train and test
  GoPro and YouTube dataset : test (generalization)
  \(\rightarrow\) spatially bicubic downsampling to make LR sequence and temporally downsampling to make lower fps sequence

• Evaluation Metrics :
  PSNR and SSIM for image quality
  tOF for temporal consistency

Comparision with SOTA

SOTA methods (SR) :
single-image SR : SwinIR [17] and HAT [18]
video SR : BasicVSR++ [1] and FTVSR [19]

SOTA methods (DB) :
single-image deblurring : Restormer [4] and FFTformer [20]
video deblurring : RVRT [6] and GShiftNet [21]

SOTA methods (VSRDB) :
HOFFR [7]

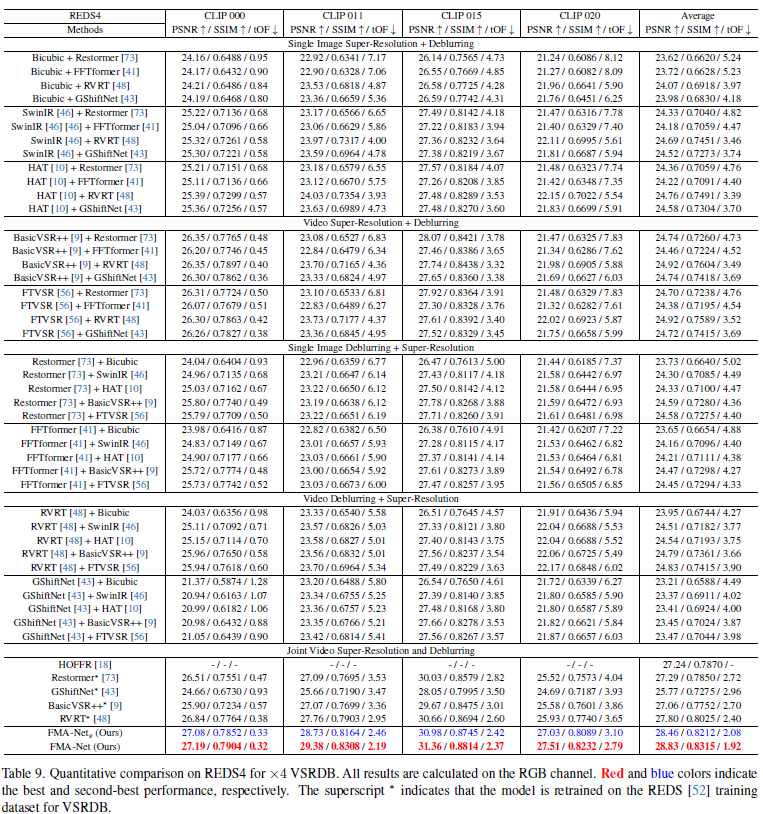
VSRDB methods have superior performance compared to sequential cascade of SR and DB
\(\rightarrow\) SR and DB tasks are highly inter-correlated

Ablation Study

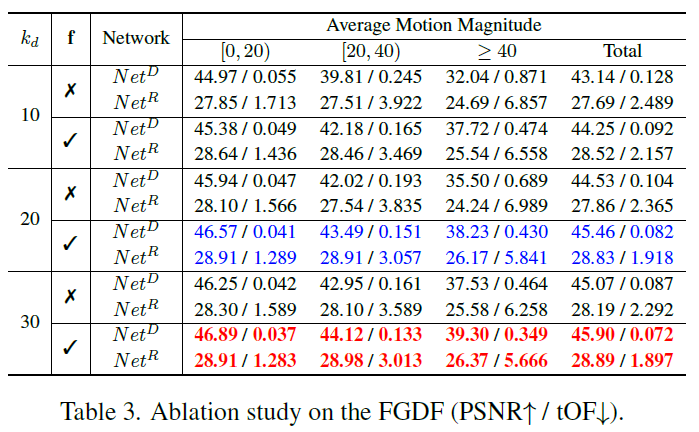
• FGDF
  FGDF is better than conventional dynamic filtering for all ranges of motion magnitudes
  conventional dynamic filtering is especially not good for large motion

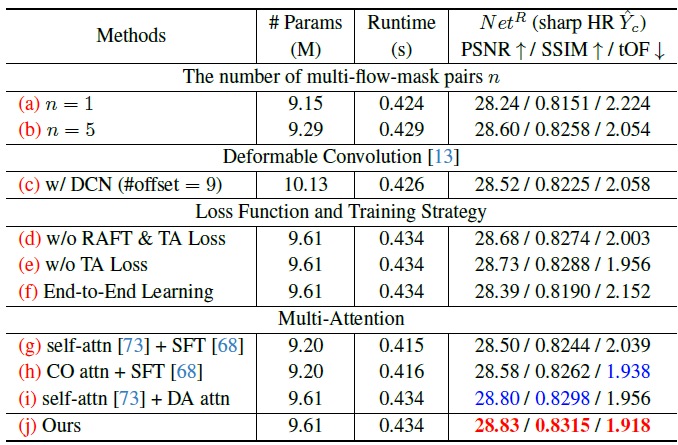
• Design of FMA-Net
  1. the number of multi-flow-mask pairs \(n\) \(\propto\) performance
  2. motion info. from multi-flow-mask pairs \(\boldsymbol f\) is better than motion info. from DCN (Deformable Conv.) due to self-induced sharper optical flows and occlusion masks
  3. RAFT loss and TA loss
  4. two-stage (\(Net^{D} \rightarrow\) both) training is better than end-to-end training
  5. multi-attention (CO + DA) is better than self-attention + SFT(spatial feature transform) [22]

SFT (spatial feature transform) [22]
ddd

---

Conclusion

VSRDB framework based on FGDF and FRMA

• FRMA :
  iteratively update features (e.g. self-induced optical flow)
  multi-attention (CO + DA attention)
• FGDF :
  predict flow-mask pair with flow-guided dynamic filters \(K^{D}\) and \(K^{R}\) that are aware of motion
  can handle large motion
• TA loss :
  temporally anchors and sharpens unwarped features
• 2-stage training :
  because, during multi-attention of \(Net^{R}\), warped feature \(F_{w}\) is adjusted by predicted degradation \(K^{D}\) from \(Net^{D}\) in globally adaptive manner

Limitation

• 2-stage approach has longer training time than end-to-end approach
• In extreme contidions such as object rotation, it is hard to predict accurate optical flow
  \(\rightarrow\) learnable homography parameters or quaternion representations can be one option to handle rotational motions