3D Gaussian Splatting
3D Gaussian Splatting for Real-Time Radiance Field Rendering (SIGGRAPH 2023)
3D Gaussian Splatting for Real-Time Radiance Field Rendering
Bernhard Kerbl, Georgios Kopanas, Thomas Leimkühler, George Drettakis
paper :
https://arxiv.org/abs/2308.04079
project website :
https://repo-sam.inria.fr/fungraph/3d-gaussian-splatting/
code :
https://github.com/graphdeco-inria/gaussian-splatting
code review :
https://semyeong-yu.github.io/blog/2024/3DGScode/
referenced blog :
https://xoft.tistory.com/51
포스팅을 시작하기에 앞서…
본 글은 직접 논문을 읽으며 정리한 내용이고
더 깔끔한 핵심 정리만 보고 싶다면
3DGS 분석1, 3DGS 분석2 글 괜찮아보임
3DGS Code 리뷰한 내 포스팅도 있음 3DGS 코드분석

Abstract
- novel 3D Gaussian scene representation with real-time differentiable renderer
수많은 3D Gaussian이 모여 scene을 구성하고 있다! - Very Fast rendering (\(\geq\) 100 FPS) :
real-time as \(\geq\) 30 FPS
rasterization이 optimization의 main bottleneck인데, 3DGS는 fast rasterization 가짐 - Higher Quality than SOTA Mip-NeRF360(2022)
- Faster Training than SOTA InstantNGP(2022)
Introduction
Why 3D Gaussian?
3D scene representation 방법
-
Mesh or Point- explicit
- good for fast GPU/CUDA-based rasterization(3D \(\rightarrow\) 2D)
-
NeRFmethod- implicit (MLP로 geometry 및 appearance를 표현)
- ray marching
- continuous coordinate-based representation
- interpolate values stored in voxels, hash grids, or points
- But,,, continuous ray로부터 discrete points를 뽑아 내는
stochastic samplingfor rendering 때문에연산량이 많고 noise생김 - MLP는 dot product 및 더하기(kernel regression)의 특성상
orthogonality를 흐리기 때문에 high-freq. output을 잘 표현할 수 없어서 따로 미리 positional encoding을 수행
-
3D Gaussianmethod- explicit (3D Gaussian으로 geometry를, SH coeff.로 appearance를 표현)
- differentiable volumetric representation
- efficient rasterization(projection and \(\alpha\)-blending)
- 3D Gaussian(ellipsoid)이나 SH coeff.라는 explicit 표현 자체가
orthogonality를 잘 살리기 때문에 high-freq. output 잘 표현 가능
Rendering (NeRF vs 3DGS)
- NeRF :
- ray per pixel 쏴서 coarse(stratified) and fine(PDF) sampling하고,
- MLP로 sampled points의 color 및 volume density를 구하고,
- 이 값들을 volume rendering 식으로 summation
- 3DGS :
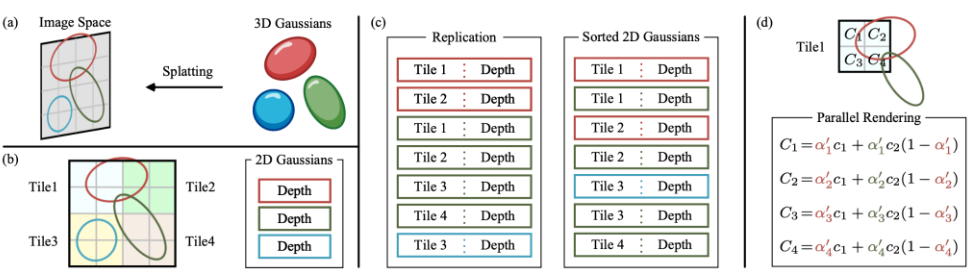
- image를 tile(14 \(\times\) 14 pixel)들로 나누고,
- tile마다 Gaussian을 Depth에 따라 정렬한 뒤
- 앞에서부터 뒤로 \(\alpha\)-blending
Related Work
생략 (추후에 다시 볼 수도)
Overview

For unbounded and complete scenes,
For 1080p high resolution and real-time(\(\geq\) 30 fps) rendering,
-
input:- Most point-based methods require
MVS(Multi-View Stereo) data,
but 3DGS only needsSfM pointsfor initialization - COLMAP 등 SfM(Structure-from-Motion) camera calibration으로 얻은
sparse point cloud에서 시작해서
scene을 3D Gaussians로 나타냄으로써
empty space에서의 불필요한 계산을 하지 않도록continuous volumetric radiance fields 정보를 저장 - NeRF-synthetic dataset의 경우 bg가 없어서 3DGS random initialization으로도 좋은 퀄리티 달성
- Most point-based methods require
-
optimizationinterleaved withadaptive density control:- optimize 4 parameters :
3D position(mean), anisotropic covariance, opacity, and spherical harmonic coeff.(color)
highly anisotropic volumetric splats는fine structures를 compact하게 나타낼 수 있음!!
spherical harmonics를 통해directional appearance(color)를 잘 나타낼 수 있음!![1] ,[2] - adaptive density control :
gradient 기반으로 Gaussian 형태를 변화시키기 위해, add and occasionally remove 3D Gaussians during optimization
- optimize 4 parameters :
- differentiable visibility-aware
real-time rendering:
perform \(\alpha\)-blending ofanisotropic splatsrespecting visibility order
by fastGPU sortingalgorithm andtile-based rasterization(projection and \(\alpha\)-blending)
한편, accumulated \(\alpha\) values를 tracking함으로써Gaussians 수에 제약 없이빠른 backward pass도 가능
Pseudo-Code

빨간 박스 : initialization
파란 박스 : optimization
초록 박스 : 특정 iter.마다 Gaussian을 clone, split, remove
Differentiable 3D Gaussian Splatting
3D Gaussian
-
differentiablevolumetric representation의 특성을 가지고 있으면서도 빠른 rendering을 위해unstructured and explicit한 게 무엇이 있을까?
\(\rightarrow\) 3D Gaussian !! -
a point를 a small planar circle with a normal이라고 가정하는 이전 Point-based rendering 논문들
[3] [4] 과 달리
SfM points는 sparse해서 normals(법선)를 estimate하기 어려울뿐만 아니라, estimate 한다 해도 very noisy normals를 optimize하는 것은 매우 어렵
\(\rightarrow\) normals 필요 없는 3D Gaussians !!
k-dim. Gaussian : \(G(\boldsymbol x) = (2\pi)^{-\frac{k}{2}}det(\Sigma)^{-\frac{1}{2}}e^{-\frac{1}{2}(\boldsymbol x - \boldsymbol \mu)^T\Sigma^{-1}(\boldsymbol x - \boldsymbol \mu)}\)
Parameters to train
-
scale vector\(s\) andquaternion\(q\) forcovariance matrix -
spherical harmonics(SH) coeff. forcolor -
opacity\(\alpha\) -
3D positionformean
Parameter 1. Covariance matrix
scale vector(scale) and quaternion(rotation) for covariance matrix
- covariance matrix는 positive semi-definite \(x^T M x \geq 0\) for all \(x \in R^n\)이어야만 physical meaning을 가지는데,
\(\Sigma\) 를 직접 바로 optimize하면 invalid covariance matrix가 될 수 있음
그렇다면!!
\(\Sigma\) 가 symmetric and positive semi-definite이도록 \(\Sigma = R S S^T R^T\) 로 정의해서
\(\Sigma\) 대신 x,y,z-axis scale을 나타내는 3D vector \(s\) 와 rotation을 나타내는 4D quaternion \(q\) 를 optimize 하자!!
quaternion에 대한 설명은 Quaternion 블로그 참고!!
-
scale3D vector \(s\)초기값:
GaussianModel().create_from_pcd()
SfM sparse point cloud의 각 점에 대해 가장 가까운 점 3개까지의 거리의 평균을 각 axis(\(x, y, z\))별로 구한 것을 3 \(\times\) 1 \(s\)라 할 때
normalize 효과를 위해 log, sqrt 씌운 뒤
3 \(\times\) 1 \(log(\sqrt{s})\) 의 값을 3번 복사하여 3 \(\times\) 3 scale matrix \(S\)를 초기화dist2 = torch.clamp_min(distCUDA2(torch.from_numpy(np.asarray(pcd.points)).float().cuda()), 0.0000001) scales = torch.log(torch.sqrt(dist2))[...,None].repeat(1, 3) -
scale3D vector \(s\)activation function:
smooth gradient 얻기 위해 exponential activation function을 씌움 -
quaternion\(q\)초기값:
각 점에 대해 \(\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}\) 으로 quaternion을 초기화하고
이를 이용하여 rotation matrix \(R = I\) 로 초기화rots = torch.zeros((fused_point_cloud.shape[0], 4), device="cuda") rots[:, 0] = 1 -
anisotropic covariance는 다양한 모양의 geometry를 나타내기 위해 optimize하기에 적합!
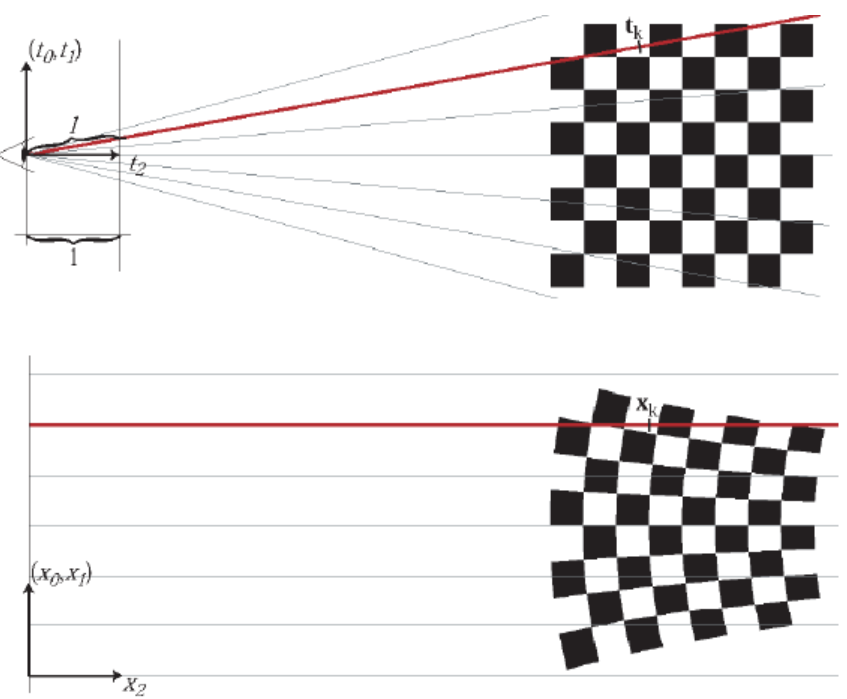
EWA volume splatting (2001)
[14] [15] :
world-to-camera 는 linear transformation 이지만,
camera-to-image (projection)는non-linear transformation이다!!
-
worldcoordinate (3D) :- \[\boldsymbol u = \begin{bmatrix} u_0 \\ u_1 \\ u_2 \end{bmatrix}\]
-
cameracoordinate (3D) :- \(\boldsymbol t = \begin{bmatrix} t_0 \\ t_1 \\ t_2 \end{bmatrix}\)
\(= W \boldsymbol u + d\)
where \(W\) :viewing transformationaffine matrix from world coordinate to camera coordinate
- \(\boldsymbol t = \begin{bmatrix} t_0 \\ t_1 \\ t_2 \end{bmatrix}\)
-
imagecoordinate (2D) :- \(\boldsymbol x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \end{bmatrix}\)
\(= \phi(\boldsymbol t) = \begin{bmatrix} \frac{t_0}{t_2} \\ \frac{t_1}{t_2} \\ \| (t_0, t_1, t_2)^T \| \end{bmatrix}\) - function \(\phi\) 는 non-linear하므로 Affine transformation이 불가능하다.
-
Local Affine (Linear) transform으로 Approx.하기 위해 \(\boldsymbol t = \boldsymbol t_{k}\) 에서의Taylor Approx.를 이용하면,
\(\phi_{k}(\boldsymbol t) = \phi(\boldsymbol t_{k}) + \boldsymbol J_{k} \cdot (\boldsymbol t - \boldsymbol t_{k})\)
where
\(\boldsymbol J_{k} = \frac{d\phi}{d \boldsymbol t}(\boldsymbol t_{k}) = \begin{bmatrix} \frac{d\phi}{d \boldsymbol t_{0}}(\boldsymbol t_{k}) & \frac{d\phi}{d \boldsymbol t_{1}}(\boldsymbol t_{k}) & \frac{d\phi}{d \boldsymbol t_{2}}(\boldsymbol t_{k}) \end{bmatrix} = \begin{bmatrix} \frac{1}{t_{k, 2}} & 0 & -\frac{t_{k, 0}}{t_{k, 2}^2} \\ 0 & \frac{1}{t_{k, 2}} & -\frac{t_{k, 1}}{t_{k, 2}^2} \\ \frac{t_{k, 0}}{l} & \frac{t_{k, 1}}{l} & \frac{t_{k, 2}}{l} \end{bmatrix}\)
and ray distance \(l = \| (t_{k, 0}, t_{k, 1}, t_{k, 2})^T \|\)
Here, \(J\) :Jacobian(각 axis로 편미분한 matrix) of theaffine approx.of theprojective transformationfrom camera coordinate to image coordinate - 즉, camera coordinate에서 임의의 좌표 \(\boldsymbol t_{k}\) 주변에 존재하는 입력 좌표 \(\boldsymbol t\)에 대해서는 image coordinate으로의 affine(linear) transformation이 충족된다.
- Gaussian Splatting 논문의 경우
Gaussian의 중심점을 \(\boldsymbol t_{k}\) 로 두면 그 주변의 \(\boldsymbol t\)에 대해서는 Jacobian을 이용한 affine(linear) transformation 가능!
- \(\boldsymbol x = \begin{bmatrix} x_0 \\ x_1 \\ x_2 \end{bmatrix}\)
Projectionof 3D Gaussiancovarianceto 2D
-
world coordinate:
\(\Sigma\) : 3 \(\times\) 3 covariance matrix of 3D Gaussian -
image coordiante(z=1) :
\(\Sigma^{\ast} = J W \Sigma W^T J^T\) : covariance matrix of 2D splat- Step 1. world-to-camera (
affine) :
\(\boldsymbol u \rightarrow W \boldsymbol u + d\) - Step 2. camera-to-image (
local affine approx.) :
Projection
\(W \boldsymbol u + d \rightarrow \phi_{k}(W \boldsymbol u + d) = x_k + \boldsymbol J_{k} W \boldsymbol u + \boldsymbol J_{k} (d - \boldsymbol t_{k})\)
상수 부분을 제외하면 \(\boldsymbol x = \boldsymbol J_{k} W \boldsymbol u\) - Step 3. covariance 특성 :
\(Cov[Ax] = E[(Ax - E[Ax])(Ax - E[Ax])^T]\)
\(= E[A(x - E[x])(x - E[x])^TA^T] = A Cov[x] A^T\) - Step 4.
world-to-image covariance:
\(\boldsymbol u \rightarrow \boldsymbol J_{k} W \boldsymbol u\) 이므로
\(\Sigma \rightarrow \boldsymbol J \boldsymbol W \Sigma \boldsymbol W^T \boldsymbol J^T\) - Step 5.
covariance dimension reduction:
추가로, \(\boldsymbol J \boldsymbol W \Sigma \boldsymbol W^T \boldsymbol J^T\) 로 계산한 \(\Sigma^{\ast}\) 는 3-by-3 matrix 인데,
3D Gaussian을 한쪽 축으로 적분하면 2D Gaussian과 동일한 값을 가지게 되므로
3-by-3 covariance matrix의 3번째 행과 열의 값을 버린
2-by-2 matrix를 projected 2D covariance matrix 로 사용!
- Step 1. world-to-camera (
param. gradient 직접 유도 (Appendix A.)
training할 때 automatic differentiation으로 인한 overhead를 방지하기 위해 param. gradient를 직접 유도함!
-
By chain rule, \(\frac{d\Sigma^{\ast}}{ds} = \frac{d\Sigma^{\ast}}{d\Sigma}\frac{d\Sigma}{ds}\) and \(\frac{d\Sigma^{\ast}}{dq} = \frac{d\Sigma^{\ast}}{d\Sigma}\frac{d\Sigma}{dq}\)
-
By covariance dimension reduction, \(\Sigma^{\ast}\) 는 \(U \Sigma U^T\) 의 좌상단 2-by-2 matrix
where \(U = JW\)
So, 편미분 값은 \(\frac{d\Sigma^{\ast}}{d\Sigma_{ij}} = \begin{bmatrix} U_{1, i} U_{1, j} & U_{1, i} U_{2, j} \\ U_{1, j} U_{2, i} & U_{2, i} U_{2, j} \end{bmatrix}\) -
For symmetric and positive semi-definite property of covariance matrix, we set \(\Sigma = MM^T\)
where \(M = RS\)
So, \(\frac{d\Sigma}{ds} = \frac{d\Sigma}{dM} \frac{dM}{ds}\) and \(\frac{d\Sigma}{dq} = \frac{d\Sigma}{dM} \frac{dM}{dq}\)
where \(\frac{d\Sigma}{dM} = 2M^T\) -
\(M = RS\)
where \(S = \begin{bmatrix} s_x & s_x & s_x \\ s_y & s_y & s_y \\ s_z & s_z & s_z \end{bmatrix}\)
So, \(\frac{dM_{i, j}}{ds_k} = \begin{cases} R_{i, k} & \text{if j=k} \\ 0 & O.W. \end{cases}\) -
\(M = RS\) and \(R(q) = \begin{bmatrix} 1 - 2 \cdot (q_j^2 + q_k^2) & 2 \cdot (q_iq_j - q_rq_k) & 2 \cdot (q_iq_k + q_rq_j) \\ 2 \cdot (q_iq_j + q_rq_k) & 1 - 2 \cdot (q_i^2 + q_k^2) & 2 \cdot (q_jq_k - q_rq_i) \\ 2 \cdot (q_iq_k - q_rq_j) & 2 \cdot (q_jq_k + q_rq_i) & 1 - 2 \cdot (q_i^2 + q_j^2) \end{bmatrix}\)
where \(q = \begin{bmatrix} q_r \\ q_i \\ q_j \\ q_k \end{bmatrix}\)
So, \(\frac{dM}{dq_r} = 2 \begin{bmatrix} 0 & -s_y q_k & s_z q_j \\ s_x q_k & 0 & -s_z q_i \\ -s_x q_j & s_y q_i & 0 \end{bmatrix}\)
and \(\frac{dM}{dq_i} = 2 \begin{bmatrix} 0 & s_y q_j & s_z q_k \\ s_x q_j & -2 s_y q_i & -s_z q_r \\ s_x q_k & s_y q_r & -2 s_z q_i \end{bmatrix}\)
and \(\frac{dM}{dq_j} = 2 \begin{bmatrix} -2 s_x q_j & s_y q_i & s_z q_r \\ s_x q_i & 0 & s_z q_k \\ -s_x q_r & s_y q_k & -2 s_z q_j \end{bmatrix}\)
and \(\frac{dM}{dq_k} = 2 \begin{bmatrix} -2 s_x q_k & -s_y q_r & s_z q_i \\ s_x q_r & -2 s_y q_k & s_z q_j \\ s_x q_i & s_y q_j & 0 \end{bmatrix}\) -
gradient for quaternion normalization is straightforward
Parameter 2. Spherical Harmonics(SH) coeff.
-
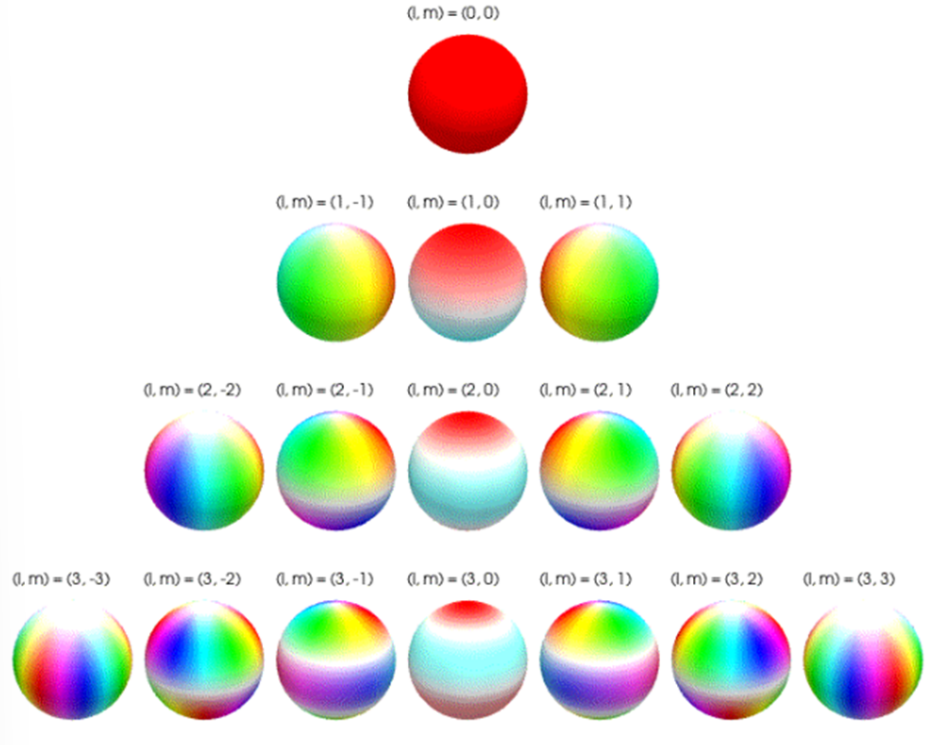
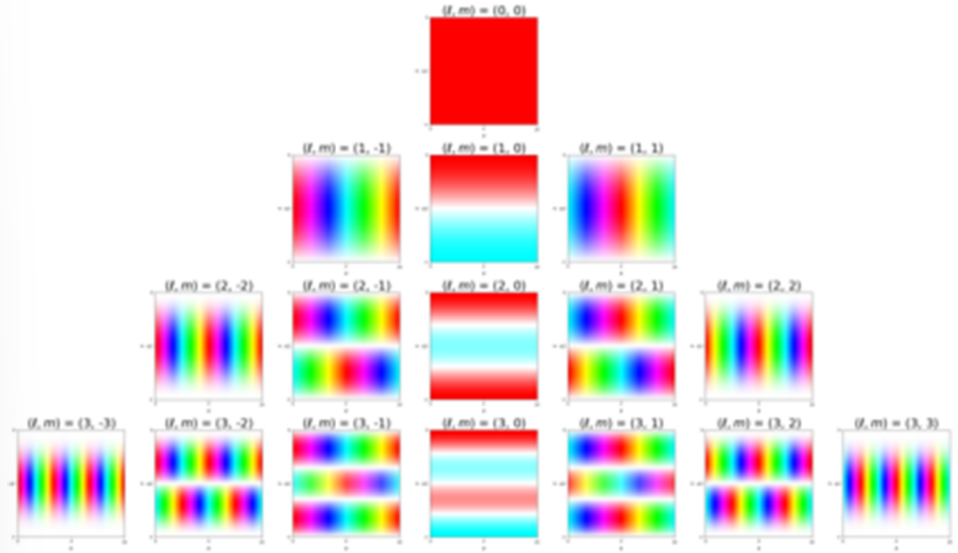
Spherical Harmonics(SH) :
spherical coordinate 에서각도(\(\theta, \phi\))를 입력받아구의 표면 위치에서의 값을 출력하는 함수
spherical coordinate 에서 라플라스 방정식을 풀면 아래 수식과 같음
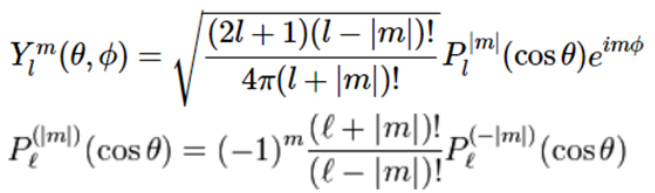
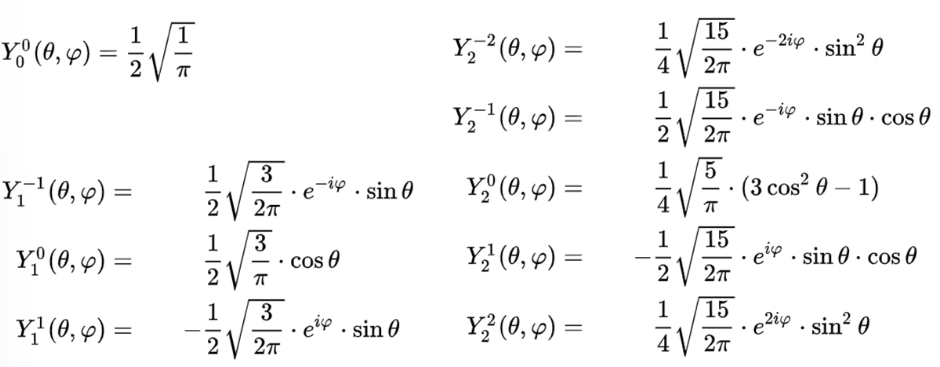
-
SH coeff.
초기값:
GaussianModel().create_from_pcd()
0-band SH (\(\theta, \phi\) 와 관계없는 view-independent color) 의 경우 SfM으로 얻은 point cloud의 RGB color값과 RGB2SH 이용하여 초기화
다른 band의 경우 0으로 초기화 - SH 의 역할 :
- SH에서 band 수를 제한해서 쓴다는 것은 높은 band (high freq. 또는 detail info.)는 자른다는 의미이므로
smoothing역할 - 적은 비용(coeff. 몇 개만 사용)으로 SH function을
approx. - Vanilla-NeRF에서는 새로운 각도(view)를 rendering할 때마다 RGB color를 얻기 위해 그때그때 MLP를 query해야 했는데,
color를 나타내기 위해 explicit SH func.을 쓸 경우
MLP를 한 번만 query 해놓으면 (SH coeff. \(k_l^m\) 을 구해놓으면)
새로운 각도(view)를 rendering할 때추가적인 MLP query 없이SH func.으로부터 바로 color 정보 얻을 수 있음
- SH에서 band 수를 제한해서 쓴다는 것은 높은 band (high freq. 또는 detail info.)는 자른다는 의미이므로
-
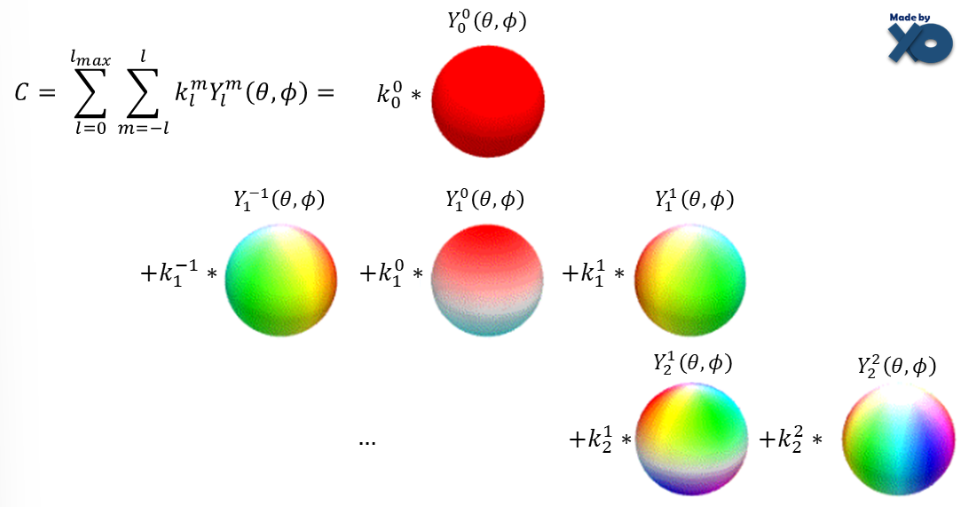
SH coeff.로color나타내는 법 :
Fourier Series 에서처럼,
SH coeff. \(k_{l}^{m}\) 의 optimal 값을 구해서
\(k_{l}^{m}\) 와 \(Y_l^m(\theta, \phi)\) 의 weighted sum!
\(C = \Sigma_{l=0}^{l_{max}} \Sigma_{m=-l}^{l} k_l^m Y_l^m(\theta, \phi)\)
즉,trainable parameter: SH coeff.인 \(k_{l}^{m}\)
(light source마다 SH coeff. \(k_{l}^{m}\) 다르므로 find optimal value)
Parameter 3. opacity
-
opacity \(\sigma\)
초기값:
임의의 실수값으로 초기화
inverse_sigmoid(0.1 * torch.ones(…)) -
opacity \(\sigma\)
range:
\(\sigma \in [0, 1)\) 위해
마지막에 sigmoid activation function을 씌워서 smooth gradient를 얻음- 3DGS 주변 위치 \(x\) 에서의 opacity : attenuated as \(\alpha = \sigma e^{- \frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu)}\)
Parameter 4. 3D position(mean)
Fast Differentiable Rasterizer for Gaussians

Tile Rasterizer
-
기능 : 3D Gaussians로 구성된 3D model을 특정 camera pose에 대해 2D rendering
-
input:- image의 rendering할 width, height
- 3D Gaussian의 xyz-mean, covariance in world-coordinate
- 3D Gaussian의 color, opacity
- current camera pose
-
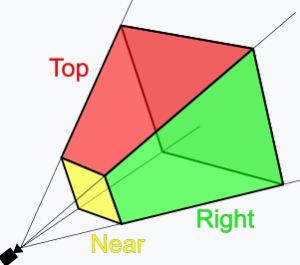
Frustum Culling:
주어진 camera pose에서 view frustum을 그려서
view frustum과 교차하는 확률이 99% confidence interval 범위 밖에 있는 3D Gaussians는 제거(culling)
-
Guard Band:
아래의 경우 projected 2D covariance 계산이 불안정하기 때문에 개별적으로 제거-
view frustum의 near plane에 가까이 있는Gaussian의 경우,
EWA Volume Splatting에서 언급된 cam-to-img projectionnonlinearity가 심하기 때문에
projection matrix를 Jacobian으로 approx.한 값에 더 큰 artifact가 생김 - view frustum 밖에 멀리 떨어진 경우
?????
코드에서는 이 경우는 빼버렸음 (주석 처리)
(diff-gaussian-rasterization/cuda_rasterizer/auxiliary.h)
-
-
Create Tiles:
CUDA 병렬 처리를 위해
\(w \times h\)의 image를 \(16 \times 16\) pixel의 tiles로 쪼갬

-
Parallelism:
tile마다개별CUDA threadblock으로 실행하여
forward/backward processing, data loading/sharing을 병렬처리
(여러 threads가 Gaussian points를 shared memory에 collaboratively load)
(VRAM과 DRAM 사이의 이동은 overhead 발생하기 때문에VRAM에서 모두 처리해버릴 수 있도록CUDA Functions(.cu)를 직접 짬!) -
Duplicate with Keys:-
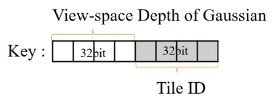
view-space-depth와tile-ID를 이용하여 tile마다 각 Gaussian의 key를 생성
tile-ID 쪽이 MSB
view-space-depth 쪽이 LSB
각 Gaussian의 value는 Gaussian’s index -
CUDA 병렬처리덕분에 2D Gaussian 하나가 3개의 tiles에 걸쳐 있다면, 3개의 2D Gaussians로 복제(instance화)되는 것처럼 작동 - tile1-depth1, tile1-depth2, tile1-depth3, tile2-depth1, tile2-depth2, … 순으로 정렬됨
-
-
Sort by Keys:
RadixSort 알고리즘 사용- tileID-depth인 key를 기준으로 정렬하므로
tile마다 Depth 기준으로 정렬됨 -
처음에 한 번sort 하고 나면 끝!! 추가로 per-pixel sorting 할 필요 없음 - parallel하게 실행하므로 single radix sort 만으로 all splats are ordered
- pixel-wise sorting이 아니라 Gaussians sort라서 \(\alpha\)-blending approx.이긴 한데,
splats가 각 pixel size 정도로 작기 때문에해당 approx. 오차는 무시 가능!??? - 쨌든 이 덕분에 visible artifacts 없이 training, rendering performance 베리베리 굳
- tileID-depth인 key를 기준으로 정렬하므로
from collections import deque
# 양방향에서 삽입/삭제 가능한 queue형 자료구조
# 1의 자릿수 기준으로 정렬한 뒤
# 10의 자릿수 기준으로 정렬한 뒤
# ...
def radixSort():
nums = list(map(int, input().split(' ')))
buckets = [deque() for _ in range(10)] # 각 자릿수(0~9)에 대응되는 10개의 empty deque()
max_val = max(nums)
queue = deque(nums) # 정렬할 숫자들
digit = 1 # 정렬 기준이 되는 자릿수
while (max_val >= digit): # 가장 큰 수의 자릿수일 때까지만 실행
while queue:
num = queue.popleft() # 정렬할 숫자
buckets[(num // digit) % 10].append(num) # 각 자릿수(0~9)에 따라 buckets에 num을 넣는다.
# 해당 정렬 기준 자릿수에서 buckets에 다 넣었으면, buckets에 담겨있는 순서대로 꺼내와서 정렬한다.
for bucket in buckets:
while bucket:
queue.append(bucket.popleft())
digit *= 10 # 정렬 기준이 되는 자릿수 증가시키기
print(list(queue))
-
Identify Tile Ranges:- tile별 Gaussian list를 효율적으로 관리하기 위해
tile마다 Gaussian ID의 범위 식별 - 이 또한
parallel하게 이루어짐
duplicated Gaussian instance마다 개별 thread를 launch하여 상위 32-bit(tile-ID)를 previous Gaussian instance와 비교
- tile별 Gaussian list를 효율적으로 관리하기 위해
-
Get Tile Ranges:
i-th tile에 대한 Gaussian list 범위 읽어옴 - \(\alpha\)-Blending in Order (
forward process) :- tile별 CUDA 병렬처리에 의해
각 pixel에 대해
color및opacity\(\alpha\) 값을 Gaussian list의앞에서 뒤로accumulate
\(c = \alpha_{1}c_{1} + (1 - \alpha_{1})(\alpha_{2}c_{2} + (1 - \alpha_{2})(\cdots)) = \alpha_{1}c_{1} + (1 - \alpha_{1})\alpha_{2}c_{2} + (1 - \alpha_{1})(1 - \alpha_{2})(\cdots) = \cdots = \sum_{i=1}^{N}(\alpha_{i}c_{i}\prod_{j=1}^{i-1}(1-\alpha_{j}))\) where \(\alpha_{0} = 0\) - i-th tile에 있는 pixels 중 a pixel’s accumulated opacity 값이 target saturation threshold를 넘어서면, 해당 i-th thread STOP (유일한 STOP 조건)
-
Gaussian의 개수를 제한하지 않음으로써 scene-specific hyper-param. tuning 없이 arbitrary depth complexity를 가지는 scene을 커버 가능
(GPU Radix Sort 덕분에 parallelism(병렬) 및 amortized(분할상환) 가능하여 Gaussian 개수 늘릴 수 있었음) -
기존 기법들은 pixel마다 정렬이 필요해서 inefficient했지만
본 논문은 tile별 CUDA 병렬처리 덕분에 efficient
(e.g. NeRF : ray per pixel 쏴서 t-distance를 pixel별로 정렬해야 함)
- tile별 CUDA 병렬처리에 의해
-
Backward process:- Gaussian의
opacity 비율에 따라뒤에서 앞으로gradient update - \(t\) -th tile 내
각 pixel에 대해
\(t\) -th tile의 Gaussian list 내 Gaussians와 (expensive) overlap testing하여 해당 pixel과 겹치는 Gaussians를 업데이트 - overhead 방지 위해 직접 backward gradient update 식을 구해서 이용
- backward process를 위해
[3] 처럼pixel마다global memory에 blended points list를 저장할 수도 있지만
dynamic memory management overhead가 생기기 때문에
forward process에서tile마다구했던 range 및 sorted Gaussian list를재사용 - \(\alpha\)-blending으로 합쳤던 각 Gaussian으로 gradient back-propagation을 해주려면
blending 각 step에서의 accumulated opacity 값이 필요한데,
이를 별도의 list에 저장해두고 훑는 게 아니라,
each point stores the final accumulated opacity in the forward process
and
divide this by each point’s opacity in our back-to-front traversal
to obtain the required coefficients for gradient computation
????? - numerical stability 위해
- 0으로 나눠지는 경우를 방지하기 위해 \(\alpha\) 값이 \(\epsilon = \frac{1}{255}\)보다 작다면 blending update 안 함
- opacity \(\alpha\) 를 upper bound 0.99로 clamp
- rasterization할 때 front-to-back blending 값 \(c\) 가 0.9999를 초과하기 전에 STOP
- Gaussian의
-
Primitives :
본 논문의 Gaussians는Euclidean space에primitives를 남김?????
\(\rightarrow\)[1] ,[10] 과 달리 distant or large Gaussians 처리를 위해 space compaction, warping, or projection 할 필요가 없음 - Efficient Rasterization :
- Pulsar 논문
[5] 에서처럼
an entire image에 대해 가장 작은 원소(primitives)를 미리 정렬(pre-sort)하여primitives = Gaussians ?????
pixel-wise sorting 비용을 절감 - differentiable
- arbitrary number of Gaussians에 대해 backpropagation 가능
with low additional memory : O(1) per pixel - 2D projection 가능
- Pulsar 논문
Optimization with Adaptive Density Control of 3D Gaussians
Optimization
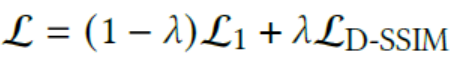
-
Loss :
predicted image와 GT image를 비교하는
L1 loss및D-SSIM loss
D-SSIM : Directional Structural Similarity Index Measure -
3D Gaussian의 xyz-mean에 대해서만
[1] 에서처럼standard exponential decay scheduling사용 - Adam optimizer로 네 가지 param. 업데이트
- 3D xyz-mean
- 3D covariance
- color
- opacity
- optimization 세부 사항 :
- 연산을
low resol.부터 warm-up:
목적 : model이 효율적으로 coarse info.부터 학습하도록 하여stability향상
초기에 4배 작은 image로 optimization 진행하고 250, 500 iter.에서 2배씩 upsampling - Spherical Harmonics
low band부터 warm-up:
목적 : 처음부터 high band로 detail까지 학습하려고 하면
scene의 corner를 촬영하거나 inside-out 방식(카메라가 촬영 대상의 내부에 위치하여 바깥쪽을 촬영) 때문에
놓친 angular 영역이 있을 경우 SH의 0-band coeff. (base or diffuse color)가 부적절하게 만들어질 수 있어서
처음에는 0-band coeff.를 optimize하고 매 1000 iter.마다 band 수 늘려서 4-band coeff.까지 optimization
- 연산을
Adaptive Density Control of Gaussians
optimization of 4 param.의 경우 매 iter.마다 update하지만,
Adaptive Density Control of Gaussians의 경우 100 iter.마다 update

-
Remove:
\(\alpha\) 값이 threshold보다 작거나
world-space에서 크기가 매우 크거나
view-space에서 footprint가 매우 큰 경우
3D Gaussians 제거
-
Gaussians가 scene을 제대로 표현 못 하는 중
\(\rightarrow\) scene을 제대로 표현하기 위해선 Gaussian position을 크게 옮겨야 함
\(\rightarrow\) view-space positional gradient \(\Delta_{p} L\)가 큼
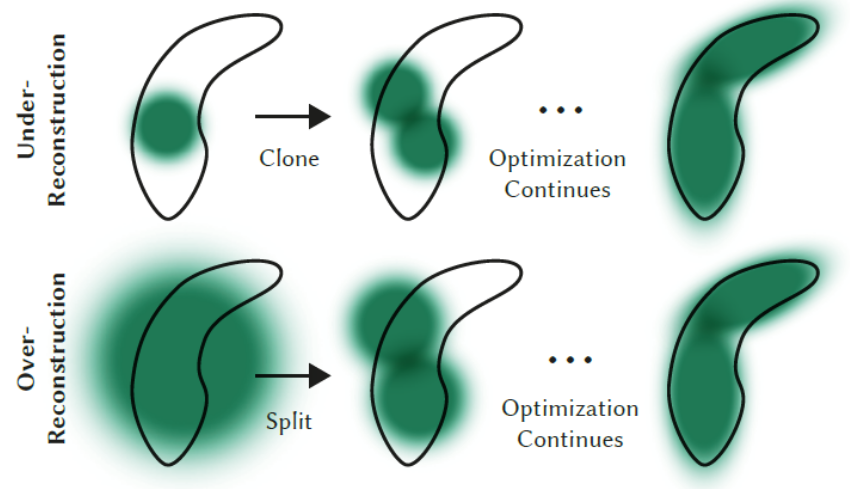
\(\rightarrow\) under/over-reconstruction 상황이므로 clone/split을 통해 정확한 위치에 Gaussian이 분포하도록 하자 -
Split:
over-reconstruction의 경우 3D Gaussians split- split : 1개의 Gaussian을
2개로 분리하고 각 scale을 줄인 후기존 3D Gaussian의 PDF에 따라 sampling하여 배치
Gaussians의 수는 증가하지만, total volume은 유지 - 조건 1.
view-space positional gradient\(\Delta_{p} L\)의 avg. magnitude \(\geq\) threshold \(\tau_{pos}\) - 조건 2.
covariance가 큼
- split : 1개의 Gaussian을
-
Clone:
under-reconstruction의 경우 3D Gaussians clone- clone :
같은 크기로 copy후positional gradient 방향에 배치
total volume 및 Gaussians의 수 모두 증가 - 조건 1.
view-space positional gradient\(\Delta_{p} L\)의 avg. magnitude \(\geq\) threshold \(\tau_{pos}\) - 조건 2.
covariance가 작음
- clone :
- 3000 iter.마다 \(\alpha\)
알파 값을 주기적으로 0으로 초기화하면 전체 Gaussian 조절에 큰 도움이 됨!- 효과 1. volumetric 기법의 특성상
camera와 가까운 영역에서 많은floater들이 생겨서 Gaussian density가 증가하는데, 이를 제거해주는 역할
floater 해결 관련 논문 :[6] [7] [8] - 효과 2.
큰 Gaussian들이 중첩되어 있는 case를 제거해주는 역할
- 효과 1. volumetric 기법의 특성상
Results
Implementation
-
custom CUDA kernel :
tile-based rasterization을 위해
custom CUDA kernel를 추가하여 사용 like[3] ,[1] ,[9] -
Radix Sort :
fast Radix Sort를 위해 NVIDIA CUB sorting routines[11] 사용 -
interactive image viewer :
open-source SIBR SIBR 이용해서
interactive image-rendering viewer 만듬 (frame rate 측정에 사용)
Evaluation
- Dataset :
bounded indoor scenes와 unbounded outdoor scenes 전부 커버- synthetic Blender dataset (Nerf) :
have exhaustive set of bounded views with exact camera param.
\(\rightarrow\) SOTA result even with 100K uniformly random initialization - Mip-Nerf360 dataset
- Tanks&Temples dataset
- Hedman et al. dataset
- synthetic Blender dataset (Nerf) :
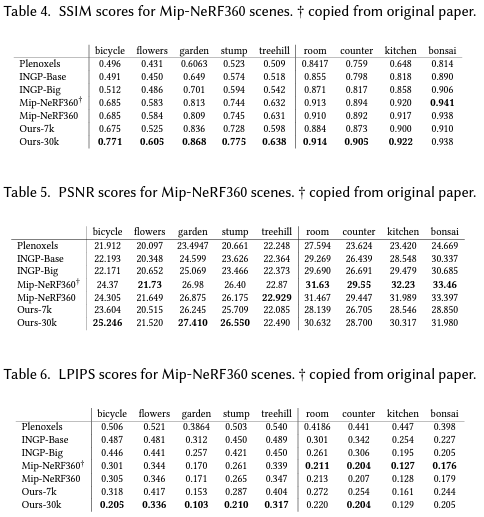
- Metrics :
- PSNR
- L-PIPS
- SSIM (D-SSIM)
- Comparison :
-
Quality: NeRF 계열 중 SOTA인Mip-Nerf360[10] 과 비교- 끝까지 훈련시켰을 때 비슷한 quality 보이고,
- training speed는 35-45 min. versus 48 hours
- Traning/Rendering
Speed: NeRF 계열 중 SOTA인InstantNGP[2] ,Plenoxels[1] 과 비교- speed SOTA인
[2] ,[1] 과 비슷한 quality 가질 때까지 training 5-10 min.밖에 안 걸리고, - 훈련 더 하면
[2] ,[1] 보다 더 좋은 quality 가짐
- speed SOTA인
-


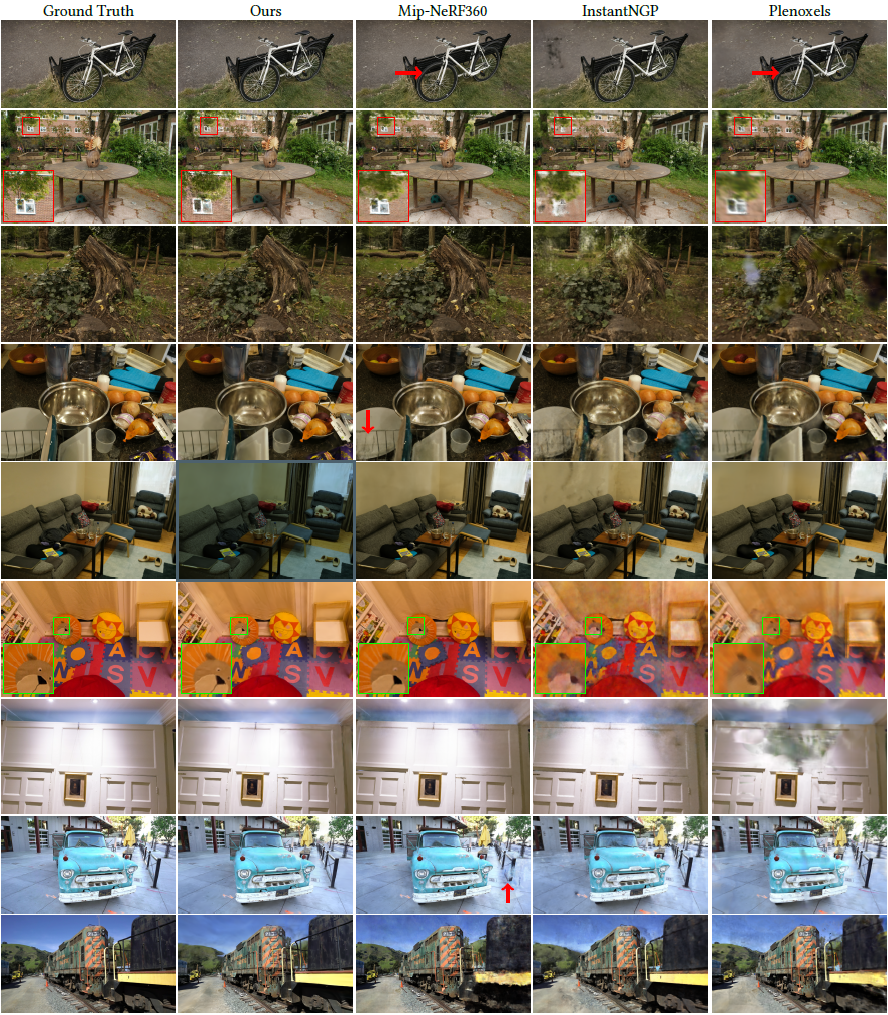
- Comparison :
- Compactness :
anisotropic 3D Gaussians는
scene representation 뿐만 아니라
complex shape with a lower number of param.을 모델링하는 데도 쓰일 수 있음- space carving으로 얻은
[12] 의 initial point cloud에서 시작했을 때[12] 의 PSNR 값은 2-4 min.만에 넘겨버림 - 또한,
[12] 의 point cloud의 4분의 1만큼만 써도 작은 model size로도[12] 의 PSNR 넘겨버림
- space carving으로 얻은
- Compactness :
Space Carving :
- 설명 : 여러 camera에 대해 voxel-space에서 object 있는 부분만 남기고 깎아내는 기법
- 이유 : 3D reconstruction을 할 때 color 정보만으로 segmentation 가능할 정도로 background는 simple할수록 좋기 때문
- 한계 : 빛, 그림자 같은 정보는 사용하지 않기 때문에 fg/bg 판단만 가능하다. 따라서 lidar처럼 camera에 depth-detection 메커니즘이 없을 경우 물체 내부의 구멍 같은 건 reconstruct 불가능
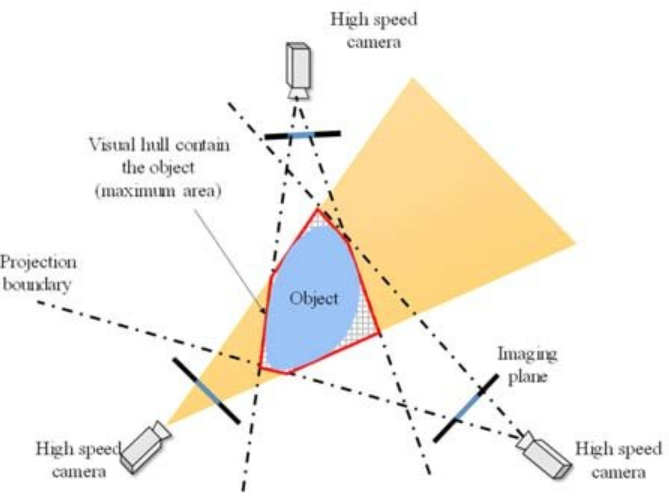
Ablation Study
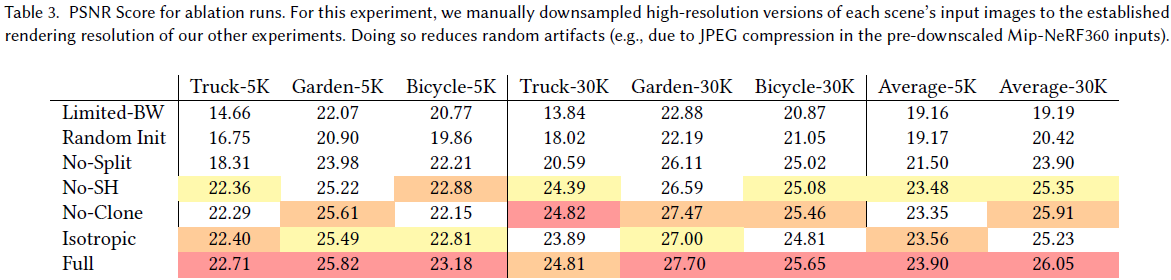
-
Intialization (SfM):- uniformly sample a cube (random initialization w/o SfM points) :
주로background퀄리티 저하
training view가 충분하지 않은 영역에서는 optimization으로 제거할 수 없는floater많이 발생
\(\rightarrow\) synthetic NeRF dataset의 경우 bg가 없고 have exhaustive set of bounded views with exact input camera param. 이므로 random initialization으로도 성능 굳
- uniformly sample a cube (random initialization w/o SfM points) :

-
Densification (clone, split):- Split :
backgroundreconstruction에 중요한 역할 - Clone :
thinstructure reconstruction에 중요한 역할
- Split :

-
Unlimited depth complexity of splats with gradients:- Limited-BW :
각 tile의 Gaussian list에서 앞에서부터 N개까지만 gradient 전파할 경우
Pulsar[5] 에서의 값의 2배인 N=10으로 했는데도 unstable optimization 초래
- Limited-BW :

-
Anisotropic Covariance:- isotropic convariance :
single scala value (radius of 3D Gaussian)를 optimize할 경우
같은 Gaussian 개수를 쓰더라도align with surfaces잘 하지 못해서finestructure 잘 나타내지 못함
- isotropic convariance :

-
Spherical Harmonics:- color 나타낼 때
view-dependenteffect 담당
- color 나타낼 때
Discussion
Limitations & Future Work
-
training view가 부족한 영역에서는 여전히floater,elongated(길쭉한) artifacts,splotchy(얼룩진) Gaussians등 artifacts 발생 (Mip-NeRF360 등 prev. methods도 마찬가지)
\(\rightarrow\) regularization으로 alleviate 가능 -
view-dependent appearance가 나타나는 영역에서는 large Gaussian 만들 때guard band등의 이유로poppingartifacts 발생
\(\rightarrow\) better culling과 regularization으로 alleviate 가능 - Gaussians
depth-order갑자기 바뀔 수 있음
\(\rightarrow\)anti-aliasing으로 해결 가능 - urban dataset처럼 very
large scene에 대해서는position learning-rate를 줄이는 게 도움됨 - prev. point-based methods에 비해서는 compact하긴 하지만, NeRF-based methods에 비해서는 memory consumption이 훨씬 큼
e.g. large scene을 학습할 때 최대 GPU memory consumption은 20GB를 넘김
\(\rightarrow\) InstantNGP에서처럼 optimization 과정을 low-level implementation 하면 괜찮
e.g. scene을 rendering할 때도 model 저장하는 데 몇백MB, rasterizer 저장하는 데 30-500MB 필요
\(\rightarrow\) memory consumption을 줄이기 위한 추후 개선 필요 (point-clouds compression technique[13] 을 적용해볼 수 있을 듯) - 3D Gaussians를 mesh reconstruction에 사용할 수 있는지 연구가 진행된다면 본 논문이 정확히 volumetric 과 surface representation 사이 어디에 위치해있는지를 이해할 수 있음


Conclusion
-
3D Gaussian:
volumetric rendering의 특성을 살림과 동시에 fast splat-based rasterization 가능
continuous representation이어야만 fast, high-quality radiance field training 가능하다는 기존 통념을 반전시킴 -
CUDAImplementation :
training time의 80%는 Pytorch code (for 가독성)
rasterization만 optimized CUDA kernels (for real-time)
\(\rightarrow\) InstantNGP[2] 처럼 optimization 나머지 부분도 전부 CUDA로 옮기면 훨씬 speedup 가능 -
real-time rasterization by GPU:
rasterization이 main bottleneck인데
GPU 힘으로 real-time rasterization pipeline 구현한 게
기존 volumetric ray-marching NeRF-based 기법보다 faster training, rendering 가능했던 비결 - Higher Quality than SOTA Mip-NeRF360(2022)
- Faster Training than SOTA InstantNGP(2022)
Question
-
Q1 :
tile-based rasterization과 parallelism의 관계를 간략히 설명해주세요 -
A1 :
tile(block)에 겹치는 2DGS들을 shared memory에 저장해서
(overlap 기준 : \(\Sigma^{\ast} = J W \Sigma W^T J^T\) 의 eigenvalue \(\times 3\))
그 tile 내에 있는 pixel(thread)들은 block shared memory(tile)에 있는 2DGS를 전부 쓰되
비교적 멀리 있는 2DGS라면 opacity의 \(e^{- \cdot}\) 항에 의해 그 pixel에는 덜 반영됨